标签:父节点 blog pre strong 排序 构建 return 一个 str
1、堆排序
是指利用 二叉堆 这种数据结构所设计的一种排序算法。堆是一个近似 完全二叉树 的结构,并同时满足 堆积的性质 :即子节点的键值或索引总是小于(或者大于)它的父节点。
完全二叉树的重要性质:
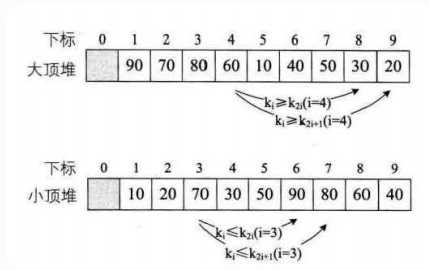
二叉堆分以下两个类型:
1.最大堆:最大堆任何一个父节点的值,都大于等于它左右孩子节点的值。[10, 8, 9, 7, 5, 4, 6, 3, 2]:
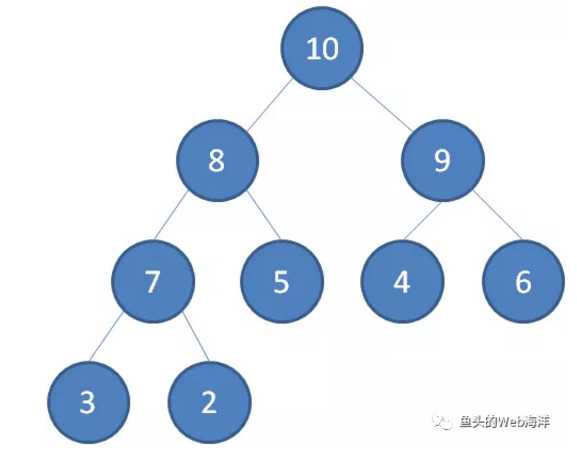
2.最小堆:最小堆任何一个父节点的值,都小于等于它左右孩子节点的值。[1, 3, 2, 6, 5, 7, 8, 9, 10]:
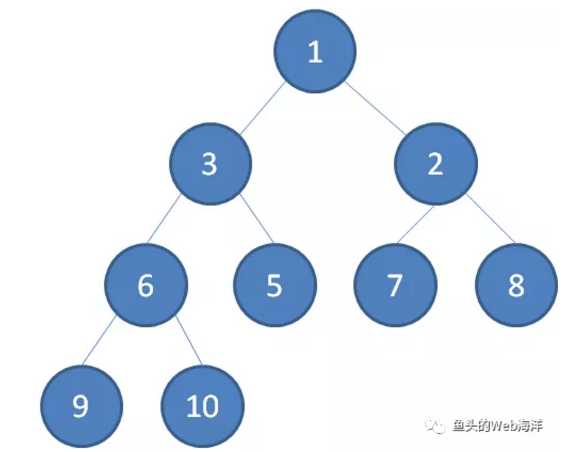
堆排序的算法步骤如下:
把无序数列构建成二叉堆;
循环删除堆顶元素,替换到二叉堆的末尾,调整堆产生新的堆顶。

void swap(int K[], int i, int j) { int temp = K[i]; K[i] = K[j]; K[j] = temp; } //大顶堆的构造,传入的i是父节点 void HeapAdjust(int k[],int p,int n) { int i,temp; temp = k[p]; for (i = 2 * p; i <= n;i*=2) //逐渐去找左右孩子结点 { //找到两个孩子结点中最大的 if (i < n&&k[i] < k[i + 1]) i++; //父节点和孩子最大的进行判断,调整,变为最大堆 if (temp >= k[i]) break; //将父节点数据变为最大的,将原来的数据还是放在temp中, k[p] = k[i]; //若是孩子结点的数据更大,我们会将数据上移,为他插入的点提供位置 p = i; //这是调整后的改变位置的子节点位置,这里可能需要再次的调整->for } //当我们在for循环中找到了p子树中,满足条件的点,我们就加入数据到该点p,注意:p点原来数据已经被上移动了 //若没有找到,就是相当于对其值不变 //插入 k[p] = temp; } //大顶堆排序 void HeapSort(int k[], int n) { int i; //首先将无序数列转换为大顶堆 for (i = n / 2; i > 0;i--) //注意由于是完全二叉树,所以我们从一半向前构造,传入父节点 HeapAdjust(k, i, n); //上面大顶堆已经构造完成,我们现在需要排序,每次将最大的元素放入最后 //然后将剩余元素重新构造大顶堆,将最大元素放在剩余最后 for (i = n; i >1;i--) { swap(k, 1, i); //逐渐将根结点(最大元素)交换至最后 HeapAdjust(k, 1, i - 1); //再次调整为最大堆 } } int main() { int i; int a[11] = {-1, 5, 2, 6, 0, 3, 9, 1, 7, 4, 8 }; HeapSort(a, 10); for (i = 1; i <= 10; i++) printf("%d ", a[i]); system("pause"); return 0; }
https://www.cnblogs.com/ssyfj/p/9512451.html
标签:父节点 blog pre strong 排序 构建 return 一个 str
原文地址:https://www.cnblogs.com/lemonzhang/p/12404839.html