标签:无向图 好的 方案 csdn col 步骤 线段 ++ 个人
目录
本系列是这本算法教材的扩展资料:《算法竞赛入门到进阶》. 罗勇军、郭卫斌. 清华大学出版社
本文web地址:https://blog.csdn.net/weixin_43914593
PDF下载地址:https://github.com/luoyongjun999/code 其中的“补充资料”
如有建议,请联系:(1)QQ 群,567554289;(2)作者QQ,15512356
??二分法和三分法是算法竞赛中常见的算法思路,本文介绍了它们的理论背景、模板代码、典型题目。
??在《计算方法》教材中,关于非线性方程的求根问题,有一种是二分法。
方程求根是常见的数学问题,满足方程:
f(x) = 0 (1-1)
的数x‘称为方程(1-1)的根。
所谓非线性方程,是指f(x)中含有三角函数、指数函数或其他超越函数。这种方程,很难或者无法求得精确解。不过,在实际应用中,只要得到满足一定精度要求的近似解就可以了,此时,需要考虑2个问题:
(1)根的存在性。用这个定理判定:设函数在闭区间[a, b]上连续,且f(a) ? f(b) < 0,则f(x) = 0存在根。
(2)求根。一般有两种方法:搜索法、二分法。
搜索法:把区间[a, b]分成n等份,每个子区间长度是?x,计算点x~k~ = a + k?x (k=0,1,2,3,4,...,n)的函数值f(x~k~),若f(x~k~) = 0,则是一个实根,若相邻两点满足f(x~k~) ? f(x~k+1~) < 0,则在(x~k~, x~k+1~)内至少有一个实根,可以取(x~k~+ x~k+1~)/2为近似根。
二分法:如果确定f(x)在区间[a, b]内连续,且f(a) ? f(b) < 0,则至少有一个实根。二分法的操作,就是把[a, b]逐次分半,检查每次分半后区间两端点函数值符号的变化,确定有根的区间。
什么情况下用二分?两个条件:上下界[a, b]确定、函数在[a, b]内单调。
??复杂度:经过n次二分后,区间会缩小到(b - a)/2^n^。给定a、b和精度要求ε,可以算出二分次数n,即满足(b - a)/2^n^ <ε。所以,二分法的复杂度是O(logn)的。例如,如果函数在区间[0, 100000]内单调变化,要求根的精度是10^-8^,那么二分次数是44次。
二分非常高效。所以,如果问题是单调性的,且求解精确解的难度很高,可以考虑用二分法。
在算法竞赛题目中,有两种题型:整数二分、实数二分。整数域上的二分,注意终止边界、左右区间的开闭情况,避免漏掉答案或者死循环。实数域上的二分,需要注意精度问题。
??先看一个简单问题:在有序数列a[]中查找某个数x;如果数列中没有x,找它的后继。通过这个问题,给出二分法的基本代码。
如果有x,找第一个x的位置;如果没有x,找比x大的第一个数的位置。


??示例:a[] = {-12,-6,-4,3,5,5,8,9},其中有n = 8个数,存储在a[0]~a[7]。
1)查找x = -5,返回位置2,指向a[2] = -4;
2)查找x = 7,返回位置6,指向a[6] = 8;
3)特别地,如果x 大于最大的a[7] = 9,例如x = 12,返回位置8。由于不存在a[8],所以此时是越界的。
下面是模板代码。
int bin_search(int *a, int n, int x){ //a[0]~a[n-1]是单调递增的
int left = 0, right = n; //注意:不是 n-1
while (left < right) {
int mid = left + (right-left)/2; //int mid = (left + right) >> 1;
if (a[mid] >= x) right = mid;
else left = mid + 1;
} //终止于left = right
return left; //特殊情况:a[n-1] < x时,返回n
}??下面对上述代码进行补充说明:
(1)代码执行完毕后,left==right,两者相等,即答案所处的位置。
(2)复杂度:每次把搜索的范围缩小一半,总次数是log(n)。
(3)中间值mid
中间值写成mid = left + (right-left)/2 或者mid = (left + right) >> 1都行 [参考李煜东《算法竞赛进阶指南》26页,有mid = (left + right) >> 1的细节解释]。不过,如果left + right很大,可能溢出,用前一种更好。
不能写成 mid = (left + right)/2; 在有负数的情况下,会出错。
(4)对比测试
bin_search()和STL的lower_bound()的功能是一样的。下面的测试代码,比较了bin_search()和lower_bound()的输出,以此证明bin_search()的正确性。注意,当a[n-1]<key时,lower_bound()返回的也是n。
代码执行以下步骤:
1)生成随机数组a[];
2)用sort()排序;
3)生成一个随机的x;
4)分别用bin_search()和lower_bound()在a[]中找x;
5)比较它们的返回值是否相同。
#include<bits/stdc++.h>
using namespace std;
#define MAX 100 //试试10000000
#define MIN -100
int a[MAX]; //如果MAX超过100万,大数组a[MAX]最好定义为全局。
//大数组定义在全局的原因是:有的评测环境,栈空间很小,大数组定义在局部占用了栈空间导致爆栈。
//现在各大OJ和比赛都会设置编译命令使栈空间等于内存大小,不会出现爆栈。
unsigned long ulrand(){ //生成一个大随机数
return (
(((unsigned long)rand()<<24)& 0xFF000000ul)
|(((unsigned long)rand()<<12)& 0x00FFF000ul)
|(((unsigned long)rand()) & 0x00000FFFul));
}
int bin_search(int *a, int n, int x){ //a[0]~a[n-1]是有序的
int left = 0, right = n; //不是 n-1
while (left < right) {
int mid = left+(right-left)/2; //int mid = (left+ right)>>1;
if (a[mid] >= x) right = mid;
else left = mid + 1;
}
return left; //特殊情况:如果最后的a[n-1] < key,left = n
}
int main(){
int n = MAX;
srand(time(0));
while(1){
for(int i=0; i< n; i++) //产生[MIN, MAX]内的随机数,有正有负
a[i] = ulrand() % (MAX-MIN + 1) + MIN;
sort(a, a + n ); //排序,a[0]~a[n-1]
int test = ulrand() % (MAX-MIN + 1) + MIN; //产生一个随机的x
int ans = bin_search(a,n,test);
int pos = lower_bound(a,a+n,test)-a;
//比较bin_search()和lower_bound()的输出是否一致:
if(ans == pos) cout << "!"; //正确
else { cout << "wrong"; break;} //有错,退出
}
}??如果只是简单地找x或x附近的数,就用STL的lower_bound()和upper_bound()函数。有以下情况:
(1)查找第一个大于x的元素的位置:upper_bound()。代码例如:
pos = upper_bound(a, a+n, test) - a;
(2)查找第一个等于或者大于x的元素:lower_bound()。
(3)查找第一个与x相等的元素:lower_bound()且 = x。
(4)查找最后一个与x相等的元素:upper_bound()的前一个且 = x。
(5)查找最后一个等于或者小于x的元素:upper_bound()的前一个。
(6)查找最后一个小于x的元素:lower_bound()的前一个。
(7)单调序列中数x的个数:upper_bound() - lower_bound()。
??寻找指定和的整数对。这是一个非常直接的二分法问题。
?问题描述
输入n ( n≤100,000)个整数,找出其中的两个数,它们之和等于整数m(假定肯定有解)。题中所有整数都能用int 表示。
?题解
下面给出三种方法:
(1)暴力搜,用两重循环,枚举所有的取数方法,复杂度O(n^2)。超时。
(2)二分法。首先对数组从小到大排序,复杂度O(nlogn);然后,从头到尾处理数组中的每个元素a[i],在a[i]后面的数中二分查找是否存在一个等于 m - a[i]的数,复杂度也是O(nlogn)。两部分相加,总复杂度仍然是O(nlogn)。
(3)尺取法/双指针/two pointers。对于这个特定问题,更好的、标准的算法是:首先对数组从小到大排序;然后,设置两个变量L和R,分别指向头和尾,L初值是0,R初值是n-1,检查a[L]+a[R],如果大于m,就让R减1,如果小于m,就让L加1,直至a[L]+a[R] = m。排序复杂度O(nlogn),检查的复杂度O(n),总复杂度O(nlogn)。检查的代码这样写:
void find_sum(int a[], int n, int m){
sort(a, a + n - 1); //先排序
int L = 0, R = n - 1; //L指向头,R指向尾
while (L < R){
int sum = a[L] + a[R];
if (sum > m) R--;
if (sum < m) L++;
if (sum == m){
cout << a[L] << " " << a[R] << endl; //打印一种情况
L++; //可能有多种情况,继续
}
}
}??上面给出的二分法代码bin_search(),处理的是简单的数组查找问题。从这个例子,我们能学习到二分法的思想。
在用二分法的典型题目中,主要是用二分法思想来进行判定。它的基本形式是:
while (left < right) {
int ans; //记录答案
int mid = left+(right-left)/2; //二分
if (check(mid)){ //检查条件,如果成立
ans = mid; //记录答案
… //移动left(或right)
}
else … //移动right(或left)
}??所以,二分法的难点在于如何建模和check()条件,其中可能会套用其他算法或者数据结构。
二分法的典型应用有:最小化最大值、最大化最小值。
??这是典型的最大值最小化问题。
?题目描述
例如,有一个序列{2,2,3,4,5,1},将其划分成3个连续的子序列S(1)、S(2)、S(3),每个子序列最少有一个元素,要求使得每个子序列的和的最大值最小。
下面举例2个分法:
分法1:S(1)、S(2)、S(3)分别是(2,2,3)、(4,5)、(1),子序列和分别是7、9、1,最大值是9;
分法2:(2,2,3)、(4)、(5,1),子序列和是7、4、6,最大值是7。
分法2更好。
?题解
在一次划分中,考虑一个x,使x满足:对任意的S(i),都有S(i)<=x,也就是说,x是所有S(i)中的最大值。题目需要求的就是找到这个最小的x。这就是最大值最小化。
如何找到这个x?从小到大一个个地试,就能找到那个最小的x。
简单的办法是:枚举每一个x,用贪心法每次从左向右尽量多划分元素,S(i)不能超过x,划分的子序列个数不超过m个。这个方法虽然可行,但是枚举所有的x太浪费时间了。
改进的办法是:用二分法在[max, sum]中间查找满足条件的x,其中max是序列中最大元素,sum是所有元素的和。
??“通往奥格瑞玛的道路”,来源:https://www.luogu.org/problem/P1462
?题目描述
给定无向图,n个点,m条双向边,每个点有点权fi(这个点的过路费),有边权ci(这条路的血量)。求起点1到终点N的所有可能路径中,在总边权(总血量)不超过给定的b的前提下,所经过的路径中最大点权(这条路径上过路费最大的那个点)的最小值是多少。
题目数据:n≤10000,m≤50000,fi,ci,B≤1e9。
?题解
对点权fi进行二分,用dijkstra求最短路,检验总边权是否小于b。二分法是最小化最大值问题。
这一题是二分法和最短路算法的简单结合。
(1)对点权(过路费)二分。题目的要求是:从1到N有很多路径,其中的一个可行路径Pi,它有一个点的过路费最大,记为Fi;在所有可行路径中,找到那个有最小F的路径,输出F。解题方案是:先对所有点的fi排序,然后用二分法,找符合要求的最小的fi。二分次数log(fi)=log(1e9) < 30。
(2)在检查某个fi时,删除所有大于fi的点,在剩下的点中,求1到N的最短路,看总边权是否小于b,如果满足,这个fi是合适的(如果最短路的边权都大于b,那么其他路径的总边权就更大,肯定不符合要求)。一次Dijkstra求最短路,复杂度是O(mlogn)。
总复杂度满足要求。
???题目描述
“进击的奶牛”,来源:https://www.luogu.org/problem/P1824
在一条很长的直线上,指定n个坐标点(x1, ..., xn)。有c头牛,安排每头牛站在其中一个点(牛棚)上。这些牛喜欢打架,所以尽量距离远一些。问最近的两头牛之间距离的最大值可以是多少。
这个题目里,所有的牛棚两两之间的距离有个最小值,题目要求使得这个最小值最大化。
?题解
(1)暴力法。从小到大枚举最小距离的值dis,然后检查,如果发现有一次不行,那么上次枚举的就是最大值。如何检查呢?用贪心法:第一头牛放在x1,第二头牛放在xj≥x1+dis的点xi,第三头牛放在xk≥xj+dis的点xk,等等,如果在当前最小距离下,不能放c条牛,那么这个dis就不可取。复杂度O(nc)。
(2)二分。分析从小到大检查dis的过程,发现可以用二分的方法找这个dis。这个dis符合二分法:它有上下边界、它是单调递增的。复杂度O(nlogn)。
#include<bits/stdc++.h>
using namespace std;
int n,c,x[100005];//牛棚数量,牛数量,牛棚坐标
bool check(int dis){ //当牛之间距离最小为dis时,检查牛棚够不够
int cnt=1, place=0; //第1头牛,放在第1个牛棚
for (int i = 1; i < n; ++i) //检查后面每个牛棚
if (x[i] - x[place] >= dis){ //如果距离dis的位置有牛棚
cnt++; //又放了一头牛
place = i; //更新上一头牛的位置
}
if (cnt >= c) return true; //牛棚够
else return false; //牛棚不够
}
int main(){
scanf("%d%d",&n, &c);
for(int i=0;i<n;i++) scanf("%d",&x[i]);
sort(x,x+n); //对牛棚的坐标排序
int left=0, right=x[n-1]-x[0]; //R=1000000也行,因为是log(n)的,很快
//优化:把二分上限设置为1e9/c
int ans = 0;
while(left < right){
int mid = left + (right - left)/2; //二分
if(check(mid)){ //当牛之间距离最小为mid时,牛棚够不够?
ans = mid; //牛棚够,先记录mid
left = mid + 1; //扩大距离
}
else
right = mid; //牛棚不够,缩小距离
}
cout << ans; //打印答案
return 0;
}??实数域上的二分,比整数二分简单。
const double eps =1e-7; //精度。如果下面用for,可以不要eps
while(right - left > eps){ //for(int i = 0; i<100; i++){
double mid = left+(right-left)/2;
if (check(mid)) right = mid; //判定,然后继续二分
else left = mid;
}??其中,循环用2种方法都可以:
while(right - left > eps) { ... }
或者:
for(int i = 0; i < 100; i++) { ... }??如果用for循环,由于循环内用了二分,执行100次,相当于实现了 1/2^100^的精度,一般比eps更精确。
for循环的100次,比while的循环次数要多。如果时间要求不是太苛刻,用for循环更简便[参考李煜东《算法竞赛进阶指南》27页的说明]。
???题目描述
“Pie”,题目来源:http://poj.org/problem?id=3122
主人过生日,m个人来庆生,有n块半径不同的圆形蛋糕,由m+1个人(加上主人)分,每人的蛋糕必须一样重,而且是一整块(不能是几个蛋糕碎块,也就是说,每个人的蛋糕都是从一块圆蛋糕中切下来的完整一块)。问每个人能分到的最大蛋糕是多大。
?题解
最小值最大化问题。设每人能分到的蛋糕大小是x,用二分法枚举x。
#include<stdio.h>
#include<math.h>
double PI = acos(-1.0); //3.141592653589793;
#define eps 1e-5
double area[10010];
int n,m;
bool check(double mid){
int sum = 0;
for(int i=0;i<n;i++) //把每个圆蛋糕都按大小mid分开。统计总数
sum += (int)(area[i] / mid);
if(sum >= m) return true; //最后看总数够不够m个
else return false;
}
int main(){
int T; scanf("%d",&T);
while(T--){
scanf("%d%d",&n,&m); m++;
double maxx = 0;
for(int i=0;i<n;i++){
int r; scanf("%d",&r);
area[i] = PI*r*r;
if(maxx < area[i]) maxx = area[i]; //最大的一块蛋糕
}
double left = 0, right = maxx;
for(int i = 0; i<100; i++){
//while((right-left) > eps) { //for或者while都行
double mid = left+(right-left)/2;
if(check(mid)) left = mid; //每人能分到mid大小的蛋糕
else right = mid; //不够分到mid大小的蛋糕
}
printf("%.4f\n",left); // 打印right也对
}
return 0;
}??饥饿的奶牛 https://www.luogu.org/problem/P1868
寻找段落 https://www.luogu.org/problem/P1419
小车问题 https://www.luogu.org/problem/P1258
借教室 https://www.luogu.org/problem/P1083
跳石头 https://www.luogu.org/problem/P2678
聪明的质监员 https://www.luogu.org/problem/P1314
分梨子 https://www.luogu.org/problem/P1493
第k大 http://acm.hdu.edu.cn/showproblem.php?pid=6231
??三分法求单峰(或者单谷)的极值,是二分法的一个简单扩展。
单峰函数和单谷函数如下图,函数f(x)在区间[l, r]内,只有一个极值v,在极值点两边,函数是单调变化的。以单峰函数为例,在v的左边,函数是严格单调递增的,在v右边是严格单调递减的。
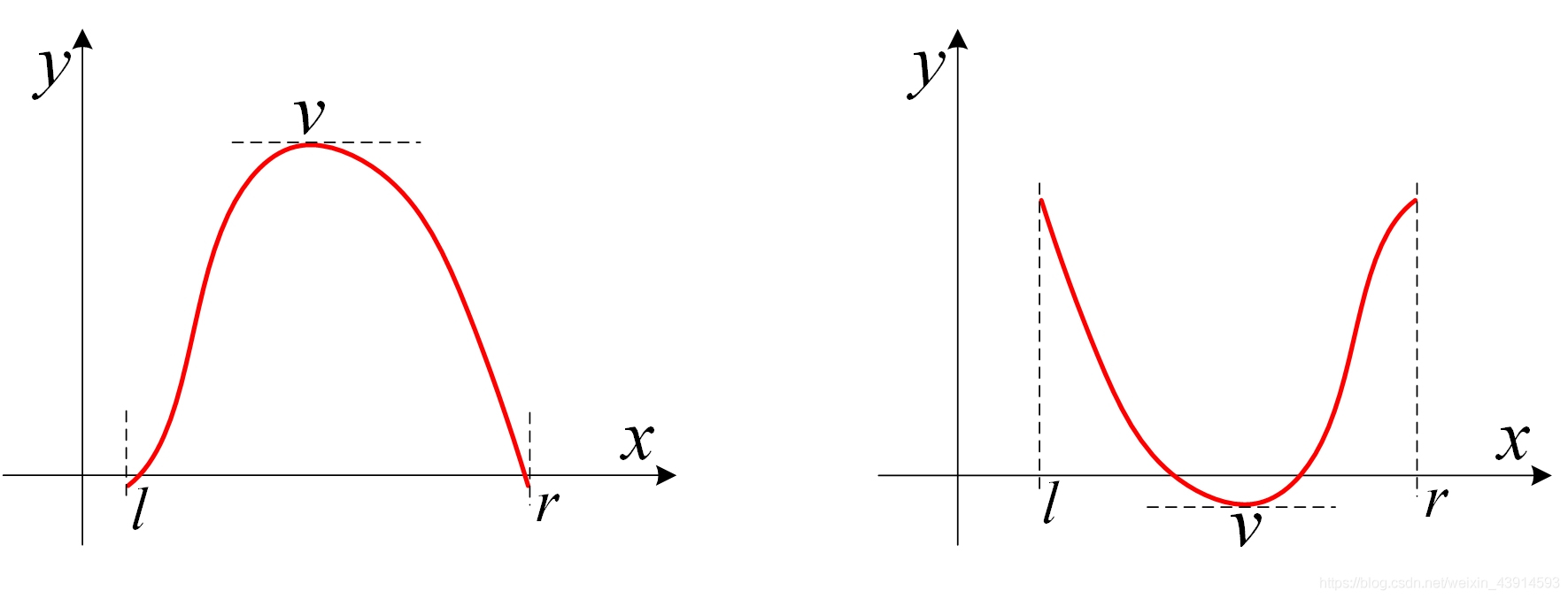
??下面的讲解都以求单峰极值为例。
如何求单峰函数最大值的近似值?虽然不能直接用二分法,不过,只要稍微变形一下,就能用了。
在[l, r]上任取2个点,mid1和mid2,把函数分成三段。有以下情况:
(1)若f(mid1) < f(mid2),极值点v一定在mid1的右侧。此时,mid1和mid2要么都在v的左侧,要么分别在v的两侧。如下图所示。
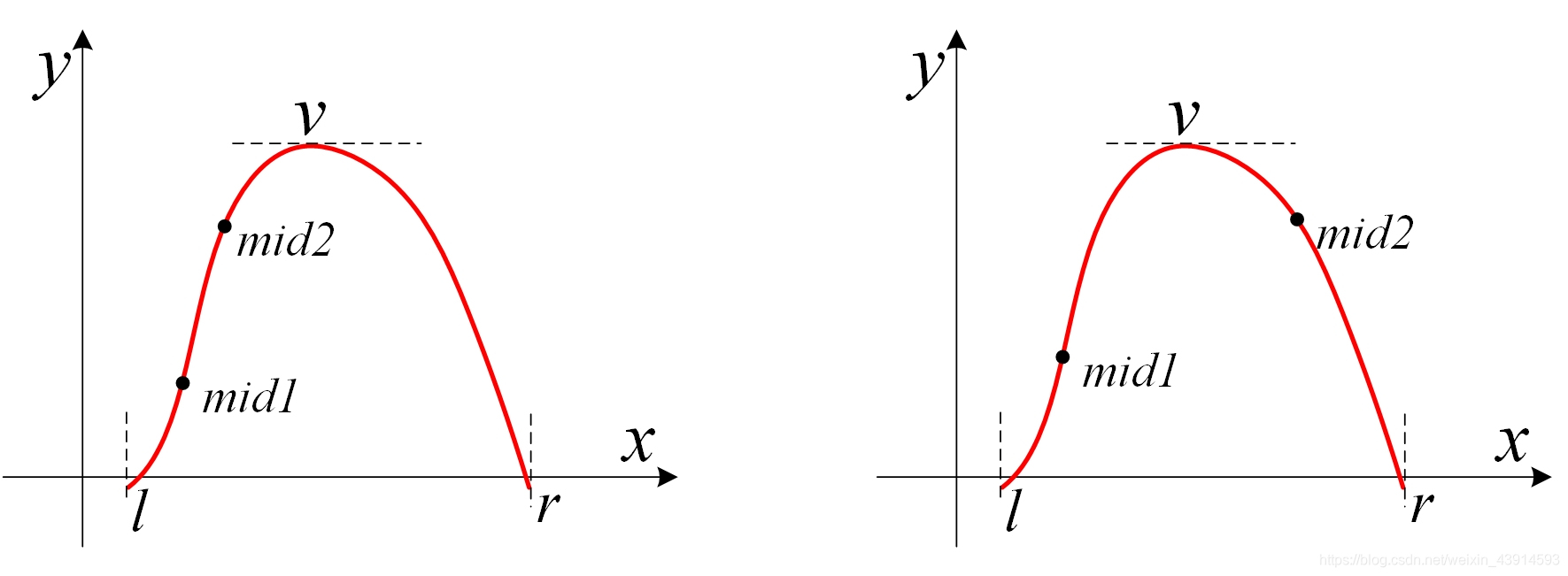
??下一步,令l = mid1,区间从[l, r]缩小为[mid1, r],然后再继续把它分成三段。
(2)同理,若f(mid1) > f(mid2),极值点v一定在mid2的左侧。如下图所示。下一步,令 r = mid2,区间从[l, r]缩小为[l, mid2]。
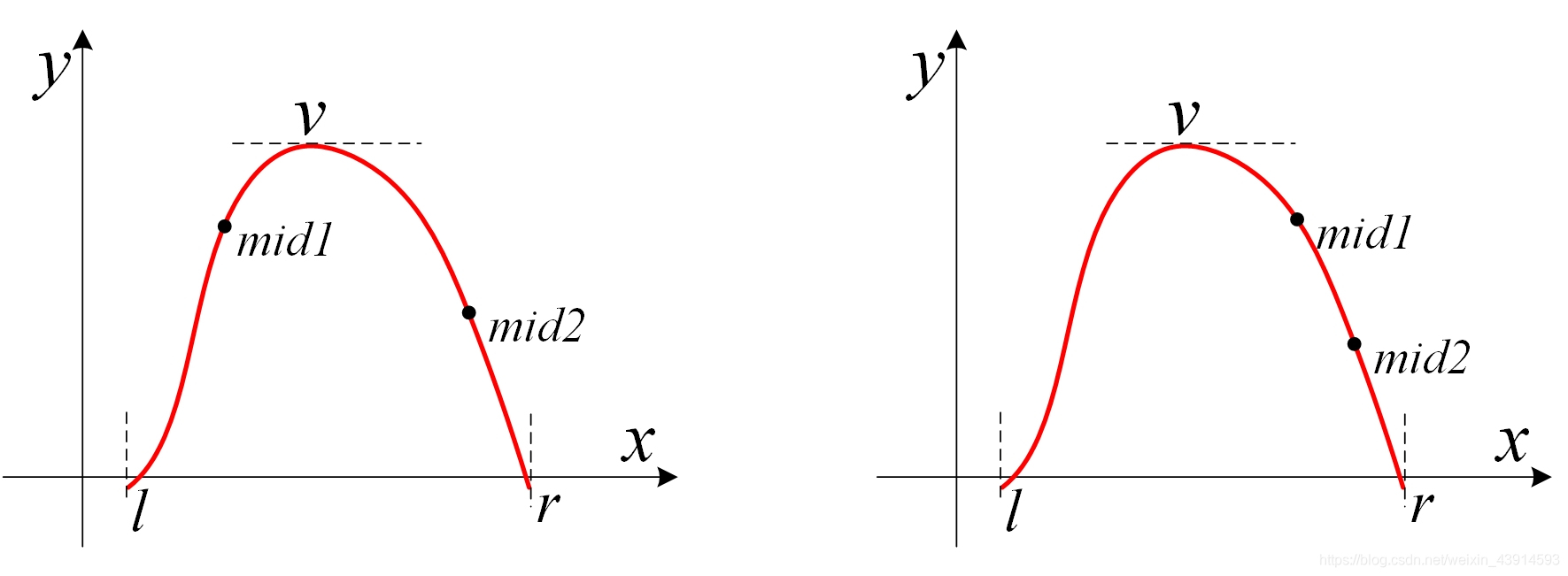
??不断缩小区间,就能使得区间[l, r]不断逼近v,从而得到近似值。
如何取mid1和mid2?有2种基本方法:
(1)三等分:mid1和mid2为[l, r]的三等分点。那么区间每次可以减少三分之一。
(2)近似三等分:计算[l, r]中间点mid = (l + r) / 2,然让mid1和mid2非常接近mid,例如mid1 = mid - eps,mid2 = mid + eps,其中eps是一个很小的值。那么区间每次可以减少接近一半。
方法(2)比方法(1)要稍微快一点。
(有网友说不要用方法(2):“因为在有些情况下这个 eps 过小可能导致这两个算出来的相等,如果相等就有可能会判断错方向,所以其实不建议这么写,log3 和 log2 本质上是一样的。”)
注意:单峰函数的左右两边要严格单调,否则,可能在一边有f(mid1) == f(mid2),导致无法判断如何缩小区间。
??下面用一个模板题给出实数三分的两种实现方法。
?题目描述
“模板三分法”,来源:https://www.luogu.com.cn/problem/P3382
给出一个N次函数,保证在范围[l, r]内存在一点x,使得[l, x]上单调增,[x, r]上单调减。试求出x的值。
?题解
下面分别用前面提到的2种方法实现:(1)三等分;(2)近似三等分。
(1)三等分
#include<bits/stdc++.h>
using namespace std;
const double eps = 1e-6;
int n;
double a[15];
double f(double x){ //计算函数值
double s=0;
for(int i=n;i>=0;i--) //注意函数求值的写法
s = s*x + a[i];
return s;
}
int main(){
double L,R;
scanf("%d%lf%lf",&n,&L,&R);
for(int i=n;i>=0;i--) scanf("%lf",&a[i]);
while(R-L > eps){ // for(int i = 0; i<100; i++){ //用for也行
double k =(R-L)/3.0;
double mid1 = L+k, mid2 = R-k;
if(f(mid1) > f(mid2))
R = mid2;
else L = mid1;
}
printf("%.5f\n",L);
return 0;
}??(2)近似三等分
#include<bits/stdc++.h>
using namespace std;
const double eps = 1e-6;
int n; double a[15];
double f(double x){
double s=0;
for(int i=n;i>=0;i--) s=s*x+a[i];
return s;
}
int main(){
double L,R;
scanf("%d%lf%lf",&n,&L,&R);
for(int i=n;i>=0;i--) scanf("%lf",&a[i]);
while(R-L > eps){ // for(int i = 0; i<100; i++){ //用for也行
double mid = L+(R-L)/2;
if(f(mid - eps) > f(mid))
R = mid;
else L = mid;
}
printf("%.5f\n",L);
return 0;
}??(1)“三分求极值”,题目来源:http://hihocoder.com/problemset/problem/1142
?题目描述:在直角坐标系中有一条抛物线y = ax^2 + bx + c和一个点P(x, y),求点P到抛物线的最短距离d。
?题解:直接求距离很麻烦。观察这一题的距离D,发现它满足单谷函数的特征,用三分法很合适。
(2)三分套三分,是计算几何的常见题型。
“Line belt”,题目来源:http://acm.hdu.edu.cn/showproblem.php?pid=3400
?题目描述:给定两条线段AB、CD ,一个人在AB上跑的时候速度是p,在CD上速度是q,在其他地方跑速度是r。问从A点到D点最少的时间。
?题解:从A出发,先走到AB上一点X,然后走到CD上一点Y,最后到D。时间是:
time = |AX|/p + |XY|/r + |YD|/q
假设已经确定了X,那么目标就是在CD上找一点Y,使|XY|/r + |YD|/q最小,这是个单峰函数。三分套三分就可以了。
??整数三分的形式是:
while (left < right) {
int mid1 = left + (right - left)/3;
int mid2 = right- (right - left)/3;
if(check(mid1) > check(mid2))
… //移动right
else
… //移动left
}??下面是一个例题。
?题目描述
“期末考试”,题目来源:https://www.lydsy.com/JudgeOnline/problem.php?id=4868
有n位同学,每位同学都参加了全部的m门课程的期末考试,都在焦急的等待成绩的公布。第i位同学希望在第ti天或之前得知所有课程的成绩。如果在第ti天,有至少一门课程的成绩没有公布,他就会等待最后公布成绩的课程公布成绩,每等待一天就会产生C不愉快度。对于第i门课程,按照原本的计划,会在第bi天公布成绩。有如下两种操作可以调整公布成绩的时间:1.将负责课程X的部分老师调整到课程Y,调整之后公布课程X成绩的时间推迟一天,公布课程Y成绩的时间提前一天;每次操作产生A不愉快度。2.增加一部分老师负责学科Z,这将导致学科Z的出成绩时间提前一天;每次操作产生B不愉快度。上面两种操作中的参数X,Y,Z均可任意指定,每种操作均可以执行多次,每次执行时都可以重新指定参数。现在希望你通过合理的操作,使得最后总的不愉快度之和最小,输出最小的不愉快度之和即可。
?题解
不愉快度是一个下凹的函数,用三分法。代码略。
标签:无向图 好的 方案 csdn col 步骤 线段 ++ 个人
原文地址:https://www.cnblogs.com/luoyj/p/12408277.html