标签:连续 利用 查找树 arc 上层 图书馆 平衡二叉树 float 特性
索引在生活中最常见的概念,无论是字典,还是图书馆藏书查找,根据索引能节约我们的时间。索引是一种为了高效获取数据的数据结构。要了解数据库索引的底层原理,我们就得先了解一种叫树的数据结构,而树中很经典的一种数据结构就是二叉树。
二叉树是每个结点最多有两个子树的树结构。通常子树被称作“左子树”(left subtree)和“右子树”(right subtree)。二叉树常被用于实现二叉查找树和二叉堆。遍历是对树的一种最基本的运算,所谓遍历二叉树,就是按一定的规则和顺序走遍二叉树的所有结点,使每一个结点都被访问一次,而且只被访问一次。遍历方式有先序遍历,中序遍历,后序遍历。


其实,B树和二叉查找树一样,B 树相当于是一棵多叉查找树,对于一棵 m 阶的 B 树具有如下规则特性:
结合规则特性,我们定义了一个节点不超过4的树,当不断新增数据的时候,树就会发现裂变。

B树不同于二叉树的是,每个节点存储的信息增多了。在计算机硬件中,我们知道每个块大块为4K,位于同一个磁盘块中的数据会被一次性读取出来。在B树数据库应用中,数据库充分利用了磁盘块的原理把节点大小限制和充分使用控制在磁盘块大小范围。,但如果数据保存的太多,每次可读取的节点信息就会减少,导致IO增多。
同时,树的节点增多后,树的层级比原来的二叉树少了,同时也减少了数据查找的次数和时间,降低了时间复杂度。
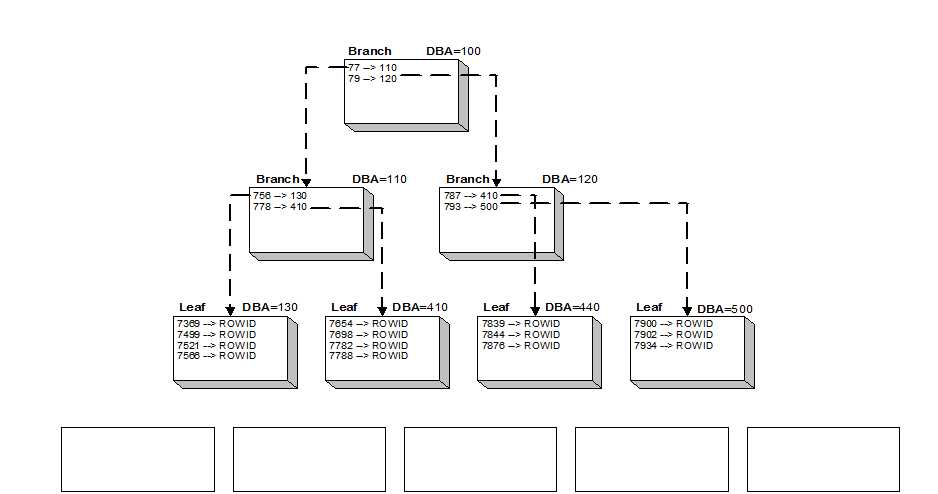
从上图看到,普通的B树的结点中,元素就是对应的数字DBA。同时在节点中,B树存放节点数据,这样我们就可以根据根节点DBA,一条条向下查找。
B+树是B树的一个升级版,相对于B树来说B+树更充分的利用了节点的空间,让查询速度更加稳定,其速度完全接近于二分法查找。为什么说B+树查找的效率要比B树更高、更稳定;我们先看看两者的区别
结合区别,我们可以看到所有的信息存储在叶子节点上,非叶子节点维护的仅是关键信息,且具体定位数据就只存储在非叶子节点中,且叶子节点有序。

所以,结合操作系统的存储逻辑块与内存读写结构,B树和B+树也有一些性能差异:
1. B树非叶子结点也保存具体数据,所以在查找某个关键字的时候找到即可返回。对于一种单一数据查询,毕竟你不需要去逐行匹配,不涉及遍历操作,幸运的情况下,有可能一次IO就能够得到你想要的结果。B树的树内存储数据,因此查询单条数据的时候,B树的查询效率不固定,最好的情况是O(1)。
2. B+Tree所有的数据都在叶子结点,并且结点之间有指针连接,在范围查询的时候,B+Tree只需要找到该关键字然后沿着链表遍历即可。但在做单一数据的查询上,其平均性能并不如B树。我们可以做一个推论:没准是Mysql中数据遍历操作比较多,所以用B+树作为索引结构。
这里可能就需要考察到Mongdb为什么用B树,而MySql用B+树知识对比了。
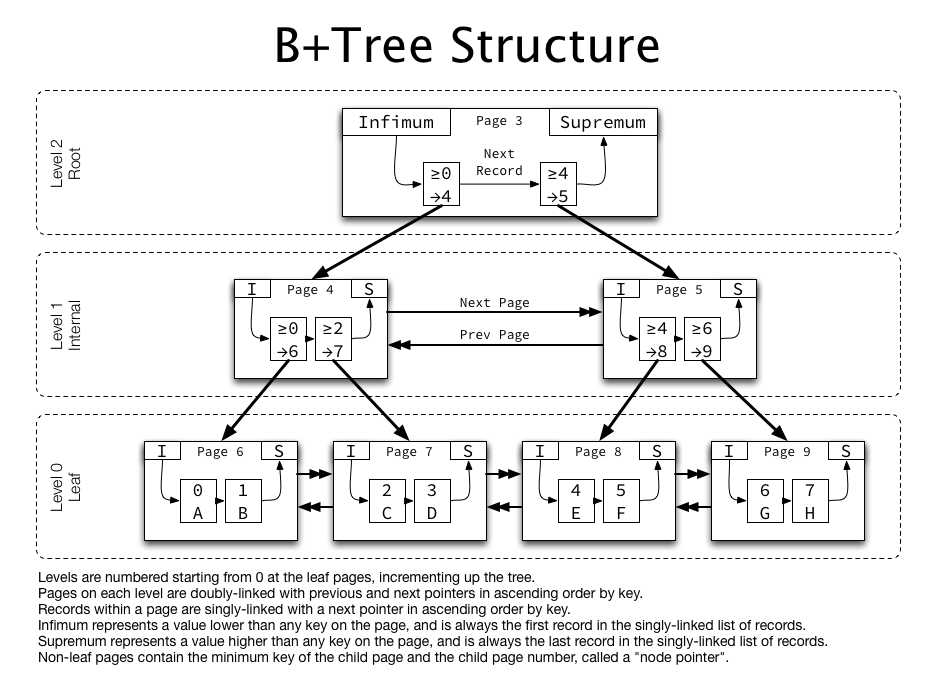
前面已经分析了B+树的存储结构,在MySql中,我们可以看到,B+树被根据等级划分,在叶子节页数据中,存储关键字一次增加。每个页之间存在双向关联。每个节点上都存在两个界限,分别是下界限(Infimum)和上界限(Supremum),下界限记录着比它小的节点关联,上界限记录着比它大的节点关联,底层子节点,包含最低界限的关键字,并且包含页码,称为节点指针。
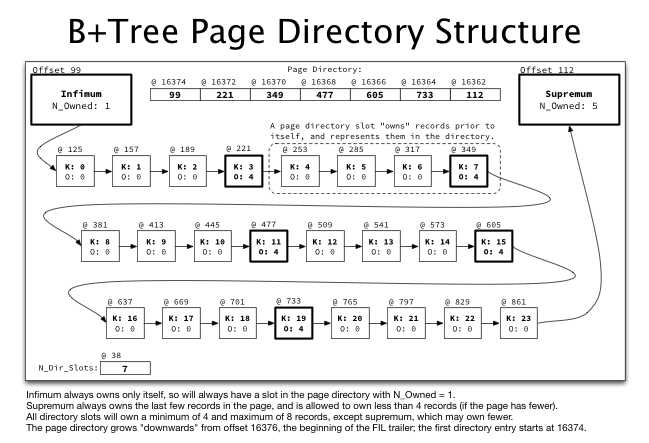
下界限总是依赖它自己,所以在也目录中它的槽为1,即N_Owned=1。上界限在页中依赖若干条记录,并且最少记录4条数据。所有页目录槽的数值范围在[4,8]。如图上层一排的结构从16376依次递减的,即为目录槽。槽内的数据是有序存放的,所以当我们寻找一条数据的时候可以先在槽中通过二分法查找到一个大致的位置。
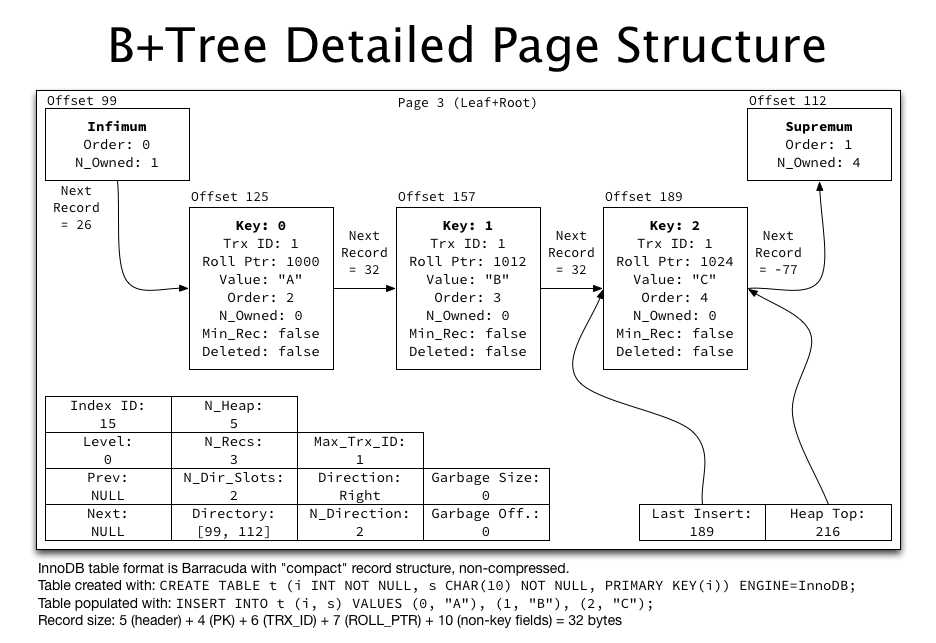
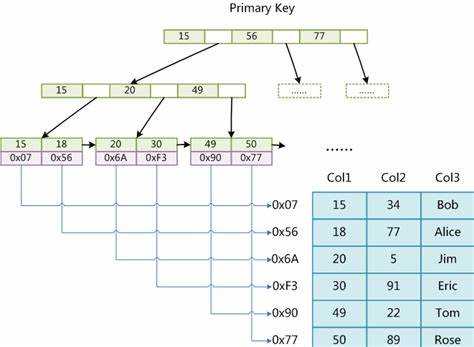
MyISAM的索引与行记录是分开存储的,叫做非聚集索引(UnClustered Index)。
其主键索引与普通索引没有本质差异:
画外音:MyISAM的表可以没有主键。
主键索引与普通索引是两棵独立的索引B+树,通过索引列查找时,先定位到B+树的叶子节点,再通过指针定位到行记录。
InnoDB的主键索引与行记录是存储在一起的,故叫做聚集索引(Clustered Index):
画外音:因此,InnoDB的PK查询是非常快的。
因为这个特性,InnoDB的表必须要有聚集索引:
(1)如果表定义了PK,则PK就是聚集索引;
(2)如果表没有定义PK,则第一个非空unique列是聚集索引;
(3)否则,InnoDB会创建一个隐藏的row-id作为聚集索引;
聚集索引,也只能够有一个,因为数据行在物理磁盘上只能有一份聚集存储。
InnoDB的普通索引可以有多个,它与聚集索引是不同的:
对于InnoDB表,这里的启示是:
(1)不建议使用较长的列做主键,因为所有的普通索引都会存储主键,会导致普通索引过于庞大;
(2)建议使用趋势递增的key做主键,由于数据行与索引一体,这样不至于插入记录时,有大量索引分裂,行记录移动;
标签:连续 利用 查找树 arc 上层 图书馆 平衡二叉树 float 特性
原文地址:https://www.cnblogs.com/weilai1917/p/12411337.html