标签:算法 大小 bdd 解释 tps 模式 制作 一个 棋盘
线性结构是最常用的数据结构,数据元素之间存在一对一的线性关系。
线性结构有两种不同的存储结构,即顺序存储结构和链式存储结构。顺序存储的线性表称为顺序表,顺序表中的存储元素是连续的。
链式存储的线性表称为链表,链表中的存储元素不一定是连续的,元素节点中存放数据元素以及相邻的地址信息。
线性表结构常见的有:数组,队列,链表,栈
非线性结构包括:二维数组,多维数组,广义表,树结构,图结构(这就不是一对一了)
定义:
当一个数组中大部分的元素为0,或为同一个值的数组时,可以使用稀疏数组来保存该数组。
eg:
可以用这种数组模拟各种棋盘,迷宫什么的.我们现在要制作一个棋盘游戏.
先不考虑这个棋怎么玩.
我们现在必须要构建出一个二维数组.
如下面所示.
*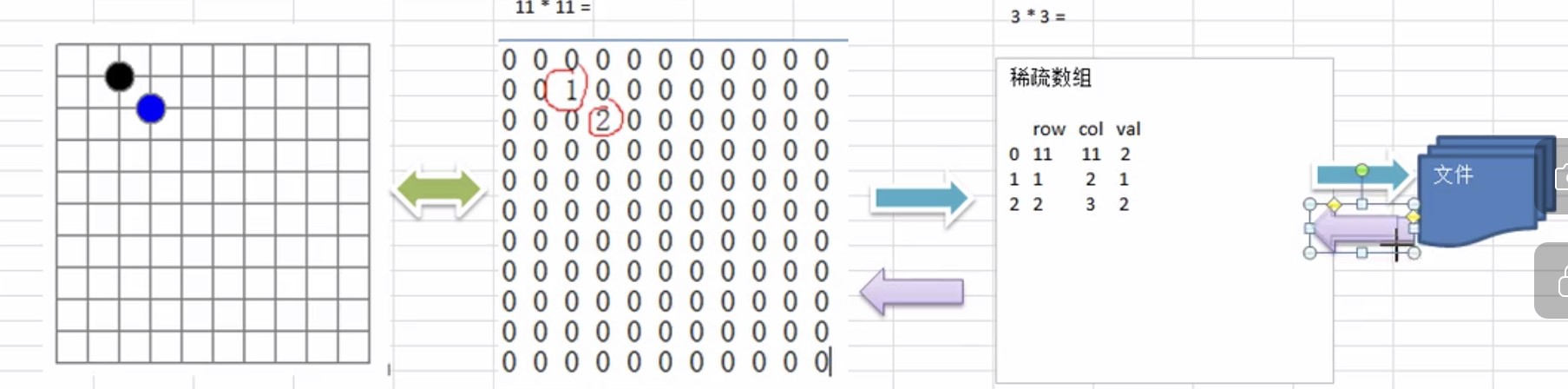
类似这个就是一个棋盘
无疑这么大的一个棋盘所需要记录的东西有点太多了,太耗费空间了,有没有简单一点的办法?
办法就是:
稀疏矩阵
回到刚才的图片中.
我们发现其中大部分的数字都是重复的,基本都是0,实际上我们真正在乎的就只有有棋子的部分就是上面那个二维数组中有1,2的节点.
| 稀疏编号 | row | col | val |
|---|---|---|---|
| 0 | 11 | 11 | 2 |
| 1 | 1 | 2 | 1 |
| 2 | 2 | 3 | 2 |
这就是图片中棋盘的稀疏矩阵(就是第二张图片的简化版本).
一个二阶数组.
用这么一个简单的方式就可以轻松的描绘出那个复杂的充满了0和1的正方形棋盘.
那我们都要记录什么内容呢
棋盘大小
上面棋子的落点
于是我们就知道了真正的问题就是如何存储这些数据.
稀疏编号为0的那一行里面保存的是关于这个棋盘的数据.
11行
11列
里面有2个棋子.
稀疏编号从1开始的那些行保存的是关于棋子的信息
稀疏数组处理的方法是:
记录数组一共有几行几列,有多少个不同的值
把具有不同值的元素的行列值记录在一个小规模的数组(稀疏数组)中,从而缩小程序的规模。
既然我们知道了这些,那么基本就可以清楚稀疏数组的运行方式:
用第一行的那个数组创建整个棋盘,用剩下的数组建立各种棋子.
那么就开始看代码吧:
首先必须知道一点,稀疏数组出现之前必须现有一个对应的二维数组(就是那个满是0与1的棋盘).
要不然这....这思维真有点厉害了.
所以我们可以先看一段制造二维数组(棋盘)的代码
//创建一个原始的二维数11*11
//0表示没有旗子,1表示黑子,2表示蓝子
//这里在程序中手动输入棋子...low一点.
int chessArr1[][] = new int[11][11];
chessArr1[1][2] = 1;
chessArr1[2][3] = 2;
//输出原始的二维数组
for (int[] row : chessArr1) {
for (int data : row) {
System.out.println("原始的二维数组");
System.out.printf("%d\t", data);
}
System.out.println();//换行用
}好了,棋盘制造完毕,这个棋盘就是图中的棋盘.
然后我们想办法将这个二位数组(棋盘)化为稀疏数组
//1.先遍历二维数组 得到非0数据的个数
int sum = 0;
for (int i = 0; i < 11; i++) {
for (int j = 0; j < 11; j++) {
if (chessArr1[i][j] != 0) {
sum++;
}
}
}
//将得到的值放入稀疏数组
int spareseArr[][] = new int[sum + 1][3];//sum是一共有多少个棋
//给稀数组赋值
//这是稀疏数组的第一行,也就是存放标准二维数组(棋盘)信息的地方
spareseArr[0][0] = 11;//有多少行
spareseArr[0][1] = 11;//有多少列
spareseArr[0][2] = sum;//必须拿到sum才能创建数组(sum在棋盘上有几个棋子)现在遍历完了数组,我们知道了第一行,现在我们要继续完成之后的行数了.
/*稀疏数组已经创建过了.spareseArr[][]
int chessArr1[][] = new int[11][11];//二维数组(棋盘)
*/
//遍历二维数组,将非0的值放到sparseArr中
int count = 0;//count 用于记录是第几个非0数据
for (int i = 0; i < 11; i++) {
for (int j = 0; j < 11; j++) {
if (chessArr1[i][j] != 0) {
//count是从1开始的,并不存在第0个棋子,但是却存在数组中的第0个元素,正好和第一行错开.
count++;//代表的是第几个棋子。 spareseArr[count]中存放的一维数组中存放的内容就是这个棋子的信息。
spareseArr[count][0] = i;//第一列,存放(非零数据)棋子在普通数组(棋盘)中的位置(行数)
spareseArr[count][1] = j;//第二列,存放(非零数据)棋子在普通数组(棋盘)中的位置(列数)
spareseArr[count][2] = chessArr1[i][j];//第三列,存放(非零数据)数据。(是黑棋蓝棋)
}
}
}就这样我们构建了第0行和剩下的稀疏矩阵.
但是我们不仅如此,虽然将那么大的一个棋盘压缩了.
但是我们还要把这个棋盘复原.
那就要将稀疏数组化为二维数组(棋盘)
//将稀疏数组--》恢复成二维数组
/**
* 1.先读取稀疏数组的第一行,根据第一行的数据,创建原始的二维数组,比如上面的chressArray
* 2.在读取稀疏数组后几行的数据,并赋给原始的二维数组即可。
*/
//1.先读取稀疏数组的第一行,根据第一行的数据,创建原始的二维数组
//稀疏数组第一列是普通二维数组的行,第二列是普通数组的列
int chessArr2[][] = new int[spareseArr[0][0]][spareseArr[0][1]];//普通数组
//2.在读取稀疏数组后几行的数据(从第二行开始),并付给原始的二维数组即可
//之所以从1开始,是因为稀疏矩阵第一行存的是普通数组的信息
for (int i=1;i<spareseArr.length;i++){
chessArr2[spareseArr[i][0]][spareseArr[i][1]]=spareseArr[i][2];
//chessArr2[spareseArr[i][0]非零数据所在行][spareseArr[i][1]非零数据所在列]=spareseArr[i][2]非零数据的值。
}
//输出恢复后的二维数组
System.out.println("恢复后的二维数组");
for (int[] row : chessArr2) {
for (int data : row) {
//关于printf相关知识:https://blog.csdn.net/qq_39017218/article/details/80042287
System.out.printf("%d\t", data);
}
System.out.println();
}
}
}
这里解释的很清楚了,就不多叙述了,这就是java算法中最简单的一种,稀疏数组.
标签:算法 大小 bdd 解释 tps 模式 制作 一个 棋盘
原文地址:https://www.cnblogs.com/yanzezhong/p/12449692.html