标签：添加   成本   lan   支持   log   比较   存储介质   solr   复杂   

提出的问题

什么情况下创建索引，什么时候不需要索引？

索引的种类有哪些？

什么是索引

索引就是帮助数据库管理系统高效获取数据的数据结构，就好比一本书的目录，它可以帮我们快速进行特定值的定位与查找，从而加快数据查询的效率。

索引的种类

从功能逻辑上划分

• 普通索引是基础的索引，没有任何约束，主要用于提高查询效率
• 唯一索引就是在普通索引的基础上增加了数据唯一性的约束，在一张数据表里可以有多个唯一索引
• 主键索引在唯一索引的基础上增加了不为空的约束，也就是 NOT NULL+UNIQUE，一张表里最多只有一个主键索引
• 全文索引用的不多，MySQL 自带的全文索引只支持英文。我们通常可以采用专门的全文搜索引擎，比如 ES(ElasticSearch) 和 Solr

从物理实现方式分

• 聚集索引
  • 聚集索引可以按照主键来排序存储数据，这样在查找行的时候非常有效
• 非聚集索引
  • 在数据库系统会有单独的存储空间存放非聚集索引，这些索引项是按照顺序存储的，但索引项指向的内容是随机存储的。也就是说系统会进行两次查找，第一次先找到索引，第二次找到索引对应的位置取出数据行，是维护单独的索引表（只维护索引，不维护索引指向的数据。
• 区别
  • 聚集索引的叶子节点存储的就是我们的数据记录，非聚集索引的叶子节点存储的是数据位置。非聚集索引不会影响数据表的物理存储顺序。
  • 一个表只能有一个聚集索引，因为只能有一种排序存储的方式，但可以有多个非聚集索引，也就是多个索引目录提供数据检索。
  • 使用聚集索引的时候，数据的查询效率高，但如果对数据进行插入，删除，更新等操作，效率会比非聚集索引低

索引的原理

索引为什么要存储在硬盘上

数据库服务器有两种存储介质，硬盘和内存，存储在内存时如果发生故障比如断点什么的，容易造成数据丢失，存储在磁盘上，会有很多的IO，我们知道磁盘IO是会耗时的，如果让索引的数据结构尽可能的减少磁盘IO操作，那么耗时就会大大减少。

从二叉树到B+树

支持快速查找的数据结构有跳表、hash表、二叉树搜索树，跳表支持区间查找，hash表不支持区间查询，二叉树搜索树不支持按照区间快速查询，但是二叉树搜索树的不断演进和改造满足了索引对数据结构的要求，下面来看看二叉搜索到B+树的演进历程。

二叉搜索树是一种比较特别大的二叉树，每个节点的左子节点都小于父节点，右子节点大于父节点，查找一个接地那的时间复杂度是O(log2n)。

iShot 2020-03-05 22.55.45.png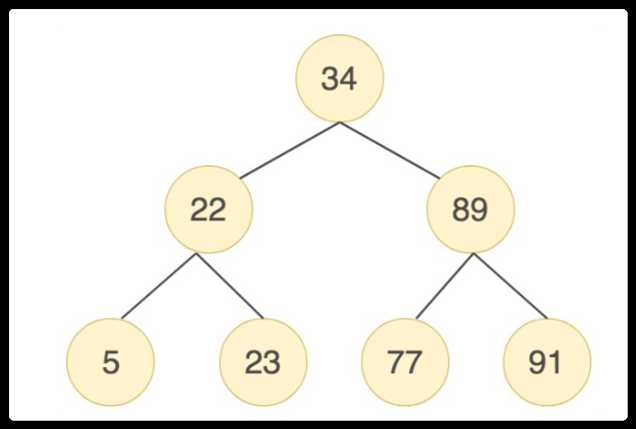

但是随着不断往树上添加节点，可能会造成一种现象，某一条路径会不断增加，最后二叉树退化成了一个链表，时间复杂度变成了O(n)。

如果能让左右子树之间的高度差不大，还能继续维持二叉搜索树的特性，大牛们提出了平衡二叉树这种结构，他让每个节点的左右子树高度差不能超过1，这属于严格平衡的，比如avl树，但是这种严格平衡的树，维护高度差需要设计复杂的算法去实现，时间成本也会增加，后来又有大牛提出，我们不让他严格平衡，高度差不要太大就行，虽然会损失一点查询速度，但是树的复杂性大大降低，查询效率也能满足要求就行，这种树就叫做红黑树。

数据查询的时间主要依赖于磁盘 I/O 的次数，如果我们采用二叉树的形式，即使通过平衡二叉搜索树进行了改进，树的深度也是 O(log2n)，当 n 比较大时，深度也是比较高的。

这个时候大牛又来了，那就该成多叉树吧，多叉树可以降低高度，这样就可以减少磁盘IO次数了，给这种树起个名字，就叫多叉平衡树，Balance Tree。那究竟该是多少个叉呢，这个是根据内存页大小计算出来的。

Balance Tree也就是B树，B树的节点是可以存储数据的，这样就会造成查询效率不稳定的情况，有时候访问到了非叶子节点就可以找到关键字，而有时需要访问到叶子节点才能找到关键字。

这个时候就又提出了B+树，B+树非叶子节点只存储索引不存数据，叶子节点才存储数据记录，叶子节点又构成一个双向链表并且从大到小顺序链接。

欢迎大家去 我的博客 瞅瞅，里面有更多关于测试实战的内容哦！！

面试测试开发被问到数据库索引不知道怎么办？这篇文章告诉你

标签：添加   成本   lan   支持   log   比较   存储介质   solr   复杂   

原文地址：https://www.cnblogs.com/zyjimmortalp/p/12454435.html