标签:开始 没有 结果 res ali mes mat tor leak
现如今图神经网络取得了很大进展,最典型的两个模型是GCN模型和GAT模型,然而现有的图神经模型仍然存在以下两个问题:
因此,这篇文章提出一个新的学习框架来增强GCN和GAT,具体的创新点可以概括为如下:
给定包含\(N\)个节点的图,\(X \in \mathbb{R}^{N \times F}\)表示节点特征,\(E \in \mathbb{R}^{N \times N \times P}\)是边特征,其中\(E_{ij\cdot}=\mathbf{0}\)表示节点\(i,j\)直接没有边连接。文章所提出的模型如下图所示:
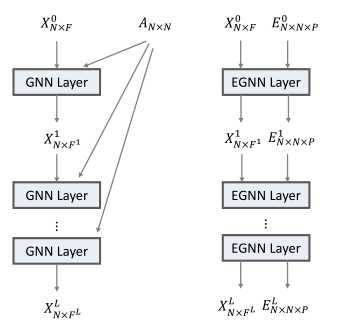
本中使用边特征乘以节点特征的方式过滤节点特征,因此为了避免乘积导致输出特征尺度发生变化,边特征需要被正则化。正则化的方式如下:
\[
\tilde{E}_{ijp} = \frac{\hat{E}_{ijp}}{\sum_{k=1}^N \hat{E}_{ikp}} \\]
\[
E_{ijp} = \sum_{k=1}^N \frac{\tilde{E}_{ikp} \tilde{E}_{jkp}}{\sum_{v=1}^N \tilde{E}_{vkp}}
\]
这样做完之后,边特征满足下面条件,即每行每列之和分别都是1:
\[
E_{ijp} \geq 0
\]
\[
\sum \limits_{i=1}^N E_{ijp} = \sum \limits_{j=1}^N E_{ijp} = 1
\]
为了利用多维边特征,这篇文章提出了如下聚合操作:
\[
X^l = \sigma \left[ \mathop{||} \limits_{p=1}^P \left(\alpha_{\cdot \cdot p}^l(X^{l-1}, E^{l-1}_{\cdot \cdot p})g^l (X^{l-1}) \right) \right]
\]
其中\(\sigma\)是激活函数,\(\alpha\)是一个产生\(N\times N \times P\)张量的函数,\(\alpha_{\cdot \cdot p}\)表示其第\(p\)个通道切片,\(g\)是节点特征变换函数。
\(\alpha^l\)就是所谓的注意力系数,\(\alpha_{ijp}\)是\(X_{i\cdot}^{l-1}\),\(X_{j\cdot}^{l-1}\)和\(E_{ijp}\)的函数,其中\(E_{ijp}\)就是边特征的第\(p\)个通道。对于多维特征,EGNN将之看作多通道信号,每一个通道会产生单独的Attention操作,不同通道结果直接连接。对于一个特定的通道\(p\),Attention操作如下:
\[
\alpha_{\cdot \cdot p}^l=DS(\tilde{\alpha}_{\cdot \cdot p}^l)
\]
\[
\tilde{\alpha}_{ijp}^l = f^l(X_{i\cdot}^{l-1},X_{j\cdot}^{l-1})E_{ijp}^{l-1}
\]
其中,\(DS\)就是双随机正则化,\(f\)可以是任何接受两个向量作为输入,输入一个标量值的Attention函数,例如:
\[
f^l(X_i^{l-1},X_j^{l-1}) = \exp \left\{ L (a^T[WX_{i\cdot}^{l-1} || WX_{j\cdot}^{l-1}]) \right\}
\]
其中\(L\)是leakyReLU,\(W\)是映射矩阵,\(||\)是连接操作。
因为文章中边特征适用于过滤节点特征的,所以对于下一层,直接将attention系数作为边特征:
\[
E^l = \alpha^l
\]
\[ X^l = \sigma \left[ \mathop{||} \limits_{p=1}^P (E_{\cdot \cdot p}X^{l-1}W^l) \right] \]
对于有向图,EGNN将通道\(E_{ijp}\)拓展成三个通道:
\[
[E_{ijp}, E_{jip}, E_{ijp} + E_{jip}]
\]
分别代表了前向,反向和无向信息。这样在编码时,节点就会从三类邻接点中聚合信息。
Exploiting Edge Features in Graph Neural Networks
标签:开始 没有 结果 res ali mes mat tor leak
原文地址:https://www.cnblogs.com/weilonghu/p/12443727.html