标签：源码   存在   存储   所有结点   实际应用   table   因子   hashmap   付出   

1 二叉排序树/二叉查找树/Binary Sort Tree

• 1种对排序和查找都很有用的特殊二叉树
• 叉排序树的弊端的解决方案：平衡二叉树
• 二叉排序树必须满足的3条性质(或是具有如下特征的二叉树)
  • 若它的左子树不为空，则：左子树上所有结点的值＜ 它根结点的值
  • 若它的右子树不为空，则：右子树上所有结点的值 > 它根结点的值
  • 它的左子树、右子树也分别为二叉排序树（递归性）

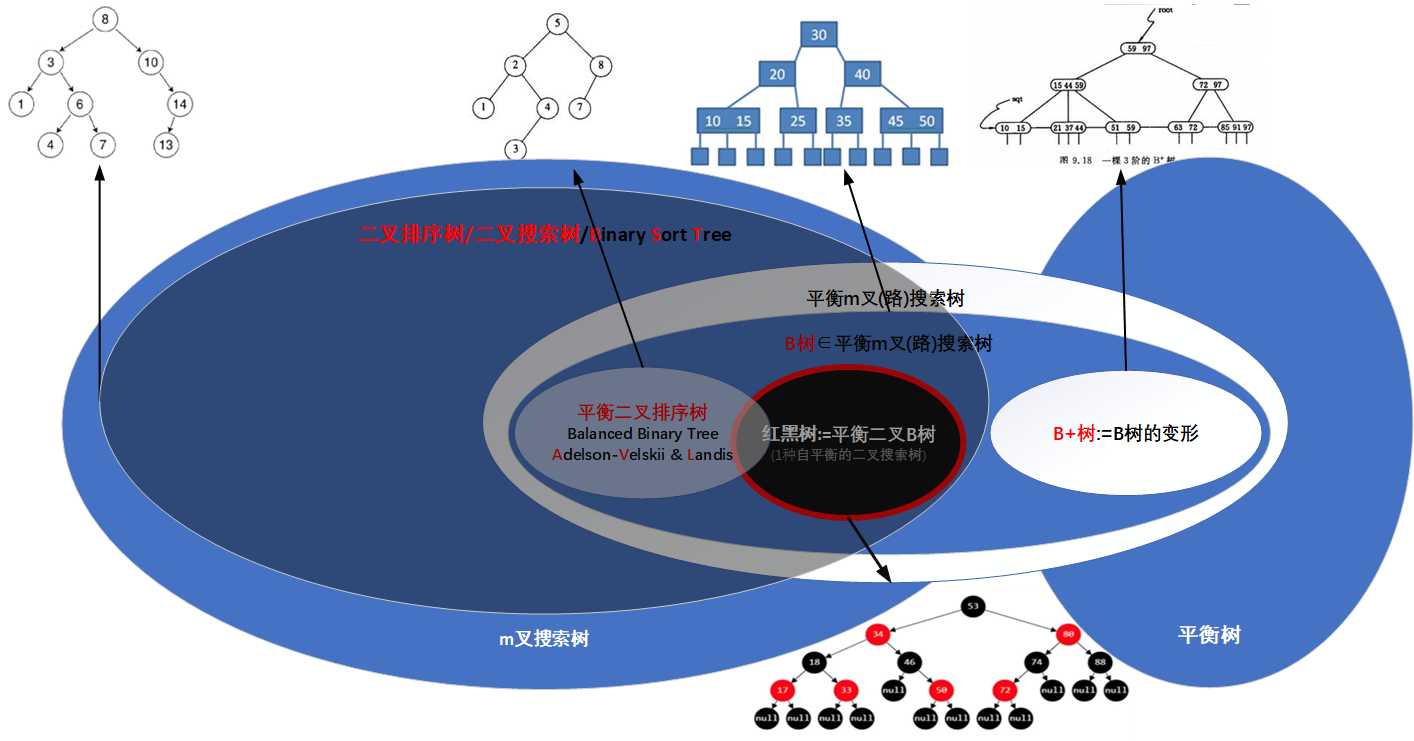
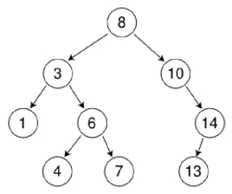
（按照如上定义，即：
1 无键值相等的结点
2 中序遍历一颗二叉树时，可得一个结点值递增的有序序列）

2 平衡二叉排序树/Balanced Binary Tree/Adelson-Velskii & Landis

• 1种结构平衡的二叉搜索树(即 叶节点高度差的绝对值不超过1)
• 平衡因子：AVL树中左子树与右子树的深度之差只能为-1、0、1
• AVL树的平衡调整方法：LL、RR、LR、RL（为了保证平衡，需付出一定代价）
• 平衡二叉树的3条性质：(AVL树or空树，或是具有如下特征的二叉排序树(BST))
  • 左子树必须为平衡二叉树
  • 右子树必须为平衡二叉树
  • |左子树深度-右子树深度|≤1

3 B树

• 1种平衡的多路搜索树，多用于文件系统、数据库的实现
• 缺点
  • 在查询单条数据是非常快的。但如果范围查的话，b树每次都要从根节点查询一遍。
• 提出者
  • 最早是由德国计算机科学家Rudolf Bayer等人于1972年在论文 《Organization and Maintenance of Large Ordered Indexes》提出的
• 结点的结构图↓
  
  
  
• 1棵m阶的B树，或为空树，或为满足下列特性的m叉树：
  • 若根结点不是叶子结点，则：有≥2棵子树
  • 树中每个结点有≤m棵子树 （m叉树的性质）
  • 所有的非终端结点有≤m-1个关键字。
  • 除根结点外的所有非终端结点有≥「m/2」棵子树

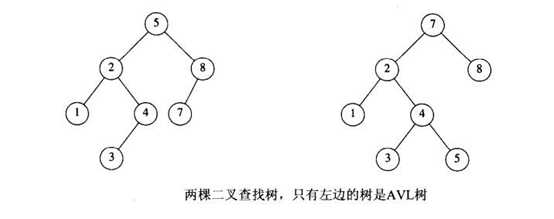
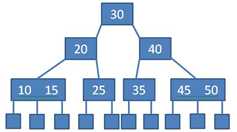
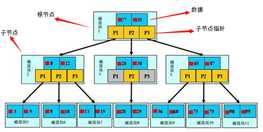
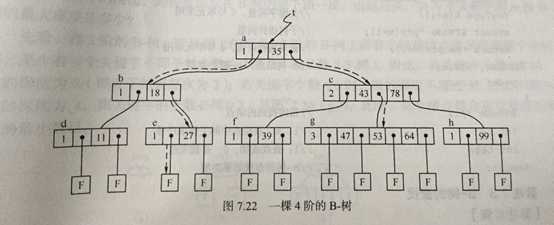
  • 所有的叶子结点都出现在同一层次上，并且不带信息（即 失败结点）

    （实质上，失败结点并不存在，指向此类结点的指针为空，引入失败结点是为便于分析B树的查找性能）

4 B+树

• 1种B树的变形树，更适合用于文件索引系统。
• 实际应用：MySQL的存储引擎InnoDB/MyISAM均利用B+树建立索引。（MYSQL-Console：SHOW INDEX FROM tableName）
• m阶B+树与m阶B树的差异
• 含有n个关键字的结点必含有n棵子树；
• 所有的非终端结点：可看成是索引部分，结点中仅含有其子树（根结点）中的最大（或最小）关键字
• 所有的叶子结点：包含了全部关键字的信息，以及指向含这些关键字记录的指针，且叶子结点本身依靠关键字的大小自小而大顺序连接；

5 红黑树/平衡二叉B树

• 别称：平衡二叉B树，1种自平衡的二叉搜索树
• 实际应用：HashMap等Java的JDK源码实现
• 红黑树必须满足的5条性质
  • 节点必为Red or Black
  • 根节点必为Black
  • 叶子节点必为Black
  • Red节点的子节点(父节点)必为Black （即 从根节点到叶子节点的所有路径上不能有2个连续的Red节点）
  • 从任一节点到叶子节点的所有路径都包含相同数目的Black节点
• 比起AVL树(平衡二叉树)，红黑树的特点↓
  
  
  

文献

• 参考：《数据结构(严蔚敏/吴伟民 - C语言 - 第2版)》
• 推荐：数据结构之B+树 - 网络博客

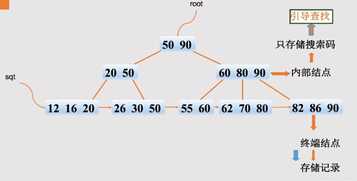
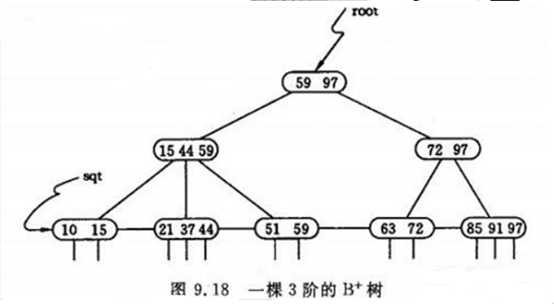
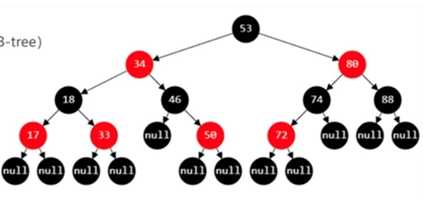
[数据结构]二叉搜索树(BST) VS 平衡二叉排序树(AVL) VS B树(平衡多路搜索树) VS B+树 VS 红黑树(平衡二叉B树)

标签：源码   存在   存储   所有结点   实际应用   table   因子   hashmap   付出   

原文地址：https://www.cnblogs.com/johnnyzen/p/12496867.html