标签:数组 分析 个数 保存 post 次数 tle 分治 非递归
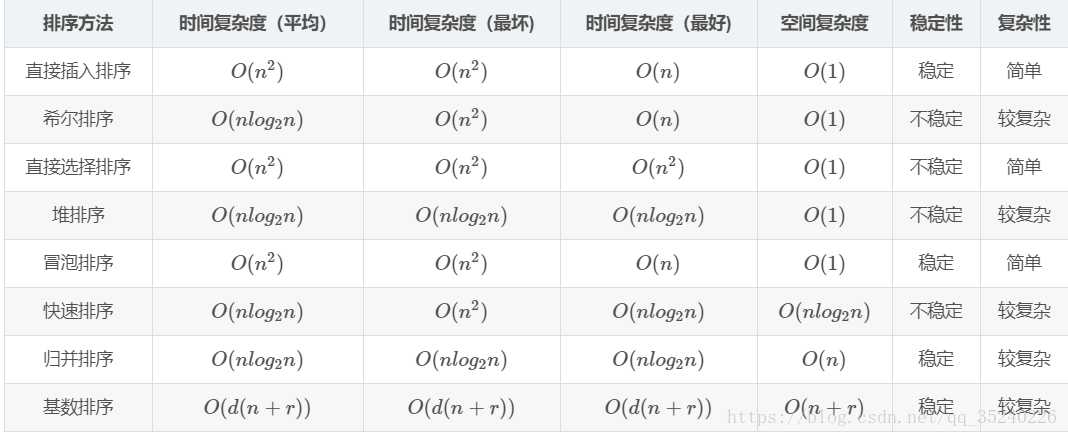
快速排序的平均时间复杂度为O(nlog n),最坏情况下为O(n2)
归并排序和希尔排序一般都比快速排序慢,其原因就在它们还在内循环中移动数据;快速排序的另一个速度优势在于它的比较次数很少。
同时快速排序是一种原地排序:
原地(原址、就地)排序是指:基本上不需要额外辅助的的空间,允许少量额外的辅助变量进行的排序。就是在原来的排序数组中比较和交换的排序。像选择排序,插入排序,希尔排序,快速排序,堆排序等都会有一项比较且交换操作(swap(i,j))的逻辑在其中,因此他们都是属于原地(原址、就地)排序,而合并排序,计数排序,基数排序等不是原地排序。
递归实现
#include <stdio.h> using namespace std; int partition(int s[],int l,int r); void quickSort(int s[],int l,int r); int main(){ int s[9]={7,5,4,6,2,3,1,9,8}; quickSort(s,0,8); for(int i=0;i<9;i++) printf("%d ",s[i]); } int partition(int s[],int l,int r){ if(l>=r) return l; int pivot=s[l];//枢纽取第一个数 while(l<r){ while(l<r && s[r]>=pivot) r--;//从右开始扫描小于枢纽的 if(l<r) s[l]=s[r];//把小值换到左边 while(l<r && s[l]<=pivot) l++; if(l<r) s[r]=s[l]; } s[l]=pivot;//挖的坑记得要填上 return l;//返回枢纽位置 } void quickSort(int s[],int l,int r){ if(l<r){ int pivotIndex= partition(s,l,r); quickSort(s,l,pivotIndex-1); quickSort(s,pivotIndex+1,r); } } //参考的是QuickSort.h源码
非递归
#include <stdio.h> #include <stack> using namespace std; int partition(int s[],int l,int r); void quickSort_stack(int s[],int n); int main(){ int s[9]={7,5,4,6,2,3,1,9,8}; quickSort_stack(s,9); for(int i=0;i<9;i++) printf("%d ",s[i]); } int partition(int s[],int l,int r){ if(l>=r) return l; int pivot=s[l];//枢纽取第一个数 while(l<r){ while(l<r && s[r]>=pivot) r--;//从右开始扫描小于枢纽的 if(l<r) s[l]=s[r];//把小值换到左边 while(l<r && s[l]<=pivot) l++; if(l<r) s[r]=s[l]; } s[l]=pivot;//挖的坑记得要填上 return l;//返回枢纽位置 } void quickSort_stack(int a[],int n){ int l=0,r=n-1; stack<int> s; s.push(l); s.push(r); while(!s.empty()){//本质上栈也是起到了保存子问题位置信息的作用 r=s.top(); s.pop(); l=s.top(); s.pop(); int privotIndex=partition(a,l,r); if(privotIndex-1>l){ s.push(l); s.push(privotIndex-1); } if(privotIndex+1<r){ s.push(privotIndex+1); s.push(r); } } }
标签:数组 分析 个数 保存 post 次数 tle 分治 非递归
原文地址:https://www.cnblogs.com/yasheng/p/12516757.html