Hyper-Parameter Optimization: A Review of Algorithms and Applications

标签：因此   优化算法   很多   好的   物体检测   spro   alt   网络   ISE   

概述

在过去的几年中，神经网络在各个领域产生了重大影响。然而，神经网络易于应用却难以训练，它可以看作是一个随机初始化的模型在大型数据集上做暴力搜索的过程。研究者们必须小心进行模型设计、算法设计以及相应的超参数选择。无免费午餐理论也说明了没有一套方法是能够解决所有问题的。

超参数是那些无法在模型训练过程中进行更新的参数，超参数优化（HPO）可以看作是模型设计的最后一步以及模型训练的第一步。超参数优化往往会导致大量计算开销，它的目的是三方面的：1）减少人工并降低学习成本；2）改进模型效率与性能；3）寻找更便利，可复现的参数集。

受到学术研究与工业应用的驱动，本文对超参数优化进行了综述，创新点包括：

• 将超参数优化系统性地分类为结构相关和训练相关两类，并讨论了它们的重要性以及实验策略。
• 在准确度、效率和适用范围方面比较分析了超参数优化算法。并根据场景论述了其不足。
• 通过比较超参数优化工具，为设计优化工具给出了建议，并分析了工具的目标人群。
• 通过现存问题展望了对算法、应用和技术的研究方向。

主要超参数和搜索空间

超参数可以分为两类：模型结构相关的超参数和模型训练相关的超参数。一组好的超参数选择能够使神经网络更快学习并达到更佳的性能。本节内容主要介绍和模型结构和训练密切相关的参数。

学习率

学习率（LR）一个是正标量，决定了SGD的步长，大多数情况下学习率需要手动调整。学习率可分为固定学习率和可变学习率，后者也就是LR schedule或LR decay。自适应的学习率能够根据模型的结构的性能进行调整，需要学习算法的支持。

常数学习率(Constant LR)最简单但却难以确定，特别是在训练快结束时，学习率可能过大。一个改进方式是将初始LR设置为0.1，当精度达到饱和时设置为0.01，并在必要时将其设置为0.001。

线性衰减(Linear LR decay)基于时间或者训练步数逐渐减小学习率，它的数学表达如下：
\[ lr = \frac{lr_0}{1+kt} \]
其中\(lr_0\)和\(k\)分别表示初始学习率和衰减速率，都是超参数。如果\(t\)是训练时间，则学习率是连续下降的，如果\(t\)是迭代次数，那么学习率一般是分段下降，每若干个迭代下降一次。两种方式的学习率曲线如下图所示。一个典型的选择是每10个epoch学习率减半，每20个epoch学习率减为1/10。

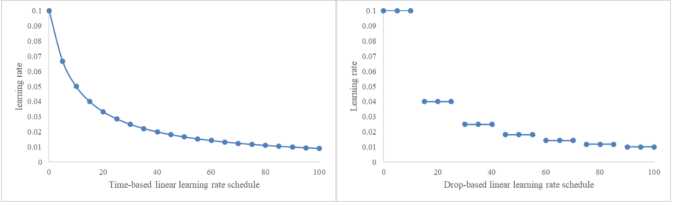
指数衰减(Exponential decay)与线性衰减相比，在初始时衰减更剧烈而在接近收敛时衰减更缓慢，如下图。它的数学表达如下：
\[ lr=lr_0 \cdot \exp(-kt) \]
其参数含义与线性衰减类似。

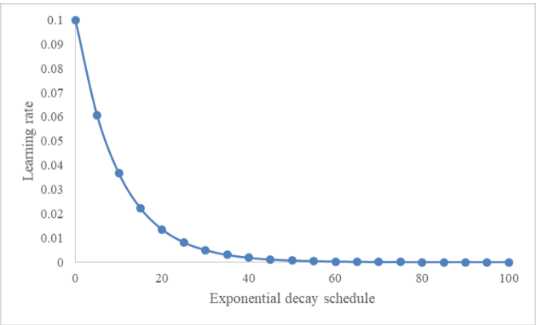
典型的LR规划(schedule)方法同样会面临两个挑战：1）用于比如在训练前决定方法中的所有超参；2）上述规划方法基于时间或者训练步数，模型中所有层共享学习率。第一个问题可以通过自动超参数调优和循环学习率(cyclical LR)方法解决，后者将为LR限定了更新上界，而该上界逐渐衰减，如下图所示。第二个问题可以通过LARS(layer-wise adaptive rate scaling)解决，网络的每一层拥有自己的学习率。

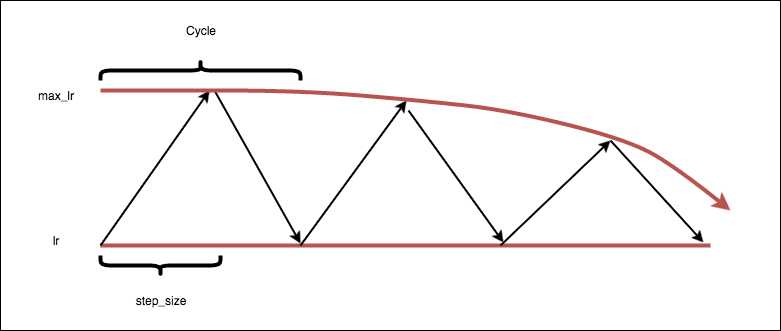
实际中，学习率和规划方法的选择具有挑战性。小学习率会导致收敛缓慢，但大学习率会导致无法收敛(如下图)，学习率通常需要和规划方法以及优化器一起调整。但也有一些规律：

• 实践中难以确定超参的重要性时，可以进行敏感性测试。
• 初始的学习率可以相对较大，这能够使得模型更快收敛。
• 使用对数缩放更新学习率，因此指数衰减一般较好。
• 常数更多的规划方法，指数衰减不一定总是最好的，这和模型与数据集有关。
  

优化器

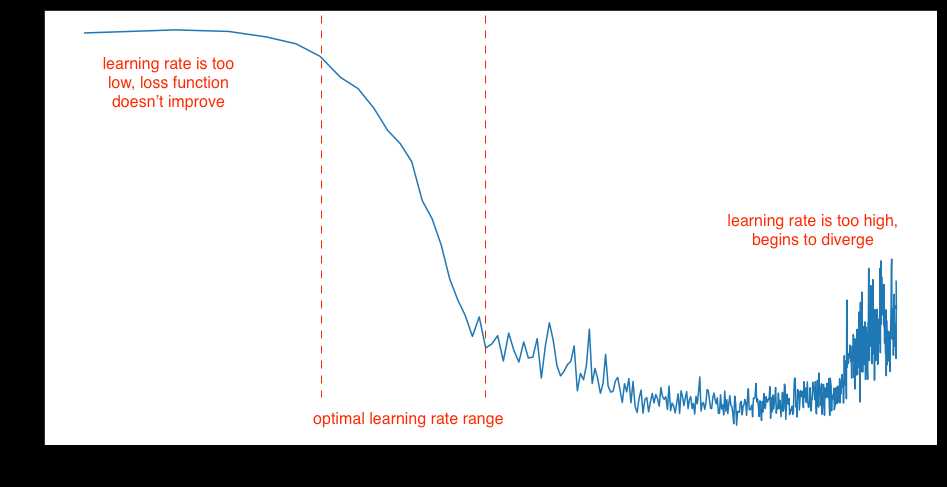
优化器，或者叫优化算法，在改进模型性能和训练速度方面扮演着重要角色。与优化器相关的超参数有优化器选择，mini-batch大小，momentum和beta。下面介绍最常用的优化器及其参数。

小批量梯度下降(mini-batch GD)与vanilla GD相比可以加速训练过程，与随机梯度下降相比能够减少噪声并易于收敛。mini-batch大小一般选择2的幂以便充分利用CPU/GPU的内存，32通常是一个默认选择。有一种观点是说，为了获得更好的性能，在其他参数固定时可以再优化mini-batch大小和学习率。不带动量的mini-batch GD收敛速度比较慢，而且容易震荡，在最近的研究中用的不是很多。

带动量的SGD可以解决震荡和收敛速度问题，它通过计算梯度的指数加权平均值来加速标准SGD，还通过为更新向量添加beta因子帮助代价函数朝正确方向下降：
\[ \begin{aligned} v_{dw} &= \beta v_{dw} + (1-\beta)v_w \w &= w - lr \cdot v_{dw} \end{aligned} \]
其中，\(w\)是权重，\(\beta\)是参数，通常设置为0.9，0.99或0.999。

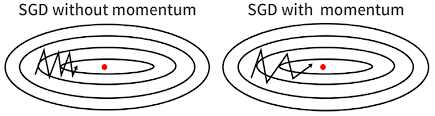
RMSprop是最常用的优化器之一，它与Adagrad和Adadelta加速梯度下降的方式类似，但在训练步数较少时体现出更优越性能。它可以看作是Rprop方法的拓展。在使用较大学习率时，RMSprop能够减慢垂直震荡并加速水平移动。RMSprop和SGD的比较如下图所示，其中，橙色曲线表示SGD，绿色曲线表示RMSprop。

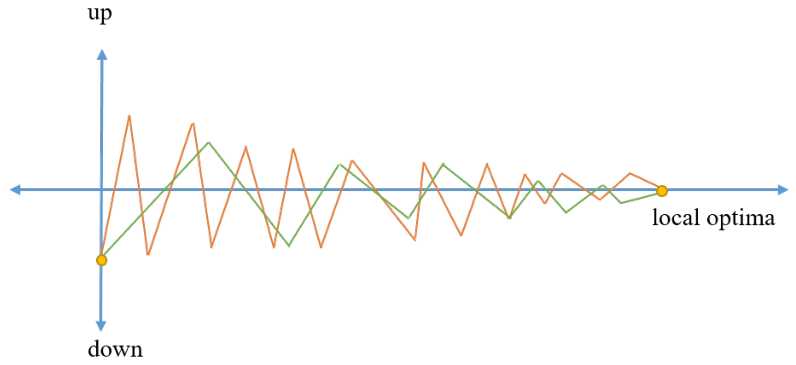
Adam(Adaptive momentum estimation)同样取得了巨大成功，作为带动量GD和RMSprop的结合，Adam在RMSprop中增加了偏差校正和动量，使其在优化的后期略胜于RMSprop。在实践中Adam通常可做为默认的优化器。它比别的优化器有更多的超参数，但通常只需要调整学习率就能够得到比较好的结果。

模型设计相关的超参数

模型深度是一个影响最终输出的关键参数，越多的层数更有可能获得更复杂的特征和更好的性能。因此在不过拟合的情况下为神经网络增加更多层往往能够提高模型容量，获得更好的结果。

模型宽度也需要被仔细考虑。一个不错的建议如下：
\[ \begin{aligned} w_{in} &\lt w \lt w_{out} \w &= \frac{2}{3}w_{in} + w_{out} \w &\lt 2 w_{out} \end{aligned} \]
其中\(w_{in}\)和\(w_{out}\)分别是输入层和输出层神经元数目。

正则化方法通常用于减少神经网络的复杂性以避免过拟合，通常使用使用如下形式：
\[ cost = lossfunction + \lambda \cdot regularizationterm \]
常用的正则化方法有\(L1\)正则化和\(L2\)正则化。\(L2\)正则化因为计算比较高效，使用更为广泛。但\(L1\)正则化可以使模型简单并提高可解释性。\(L1\)和\(L2\)正则化的利弊如图所示：

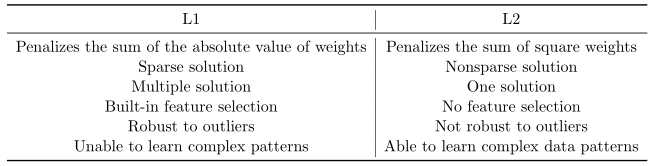
数据增强也是常用的正则化手段，它通过创建假样本并加入到训练集中从而避免过拟合。这在CV领域的图片分类和物体检测上比较常见。

Dropout也是不得不说的正则化方法，它通过以一定概率随机挑选神经元参与训练，使得网络对于特定权重不那么敏感。Dropout的概率通常设置为0.2到0.5，太大的概率可能过于简化模型，而太小的概率又会导致dropout没有效果。另外，使用dropout时，通常可以使用更大的学习率和动量，因为此时参与更新的神经元减少了。

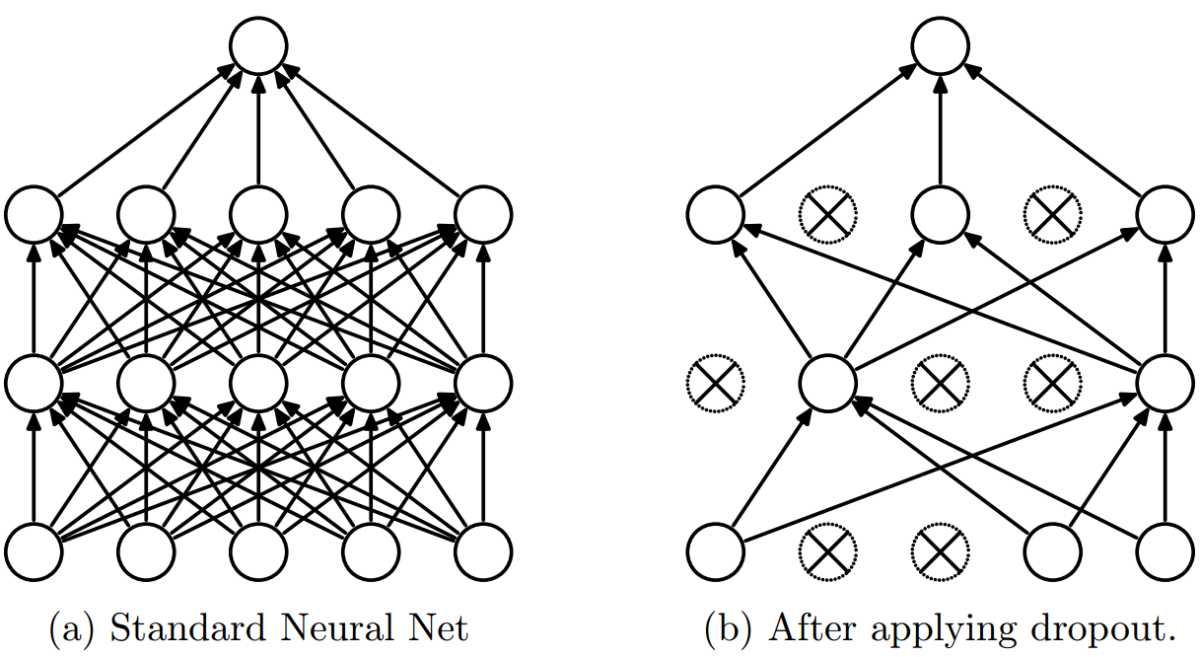
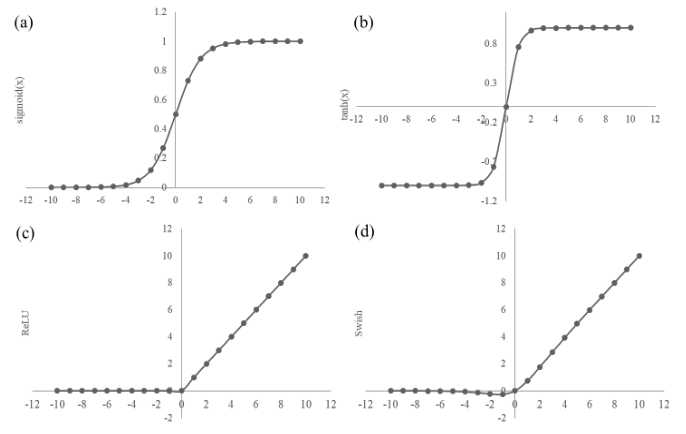
激活函数为深度学习引入非线性，如果没有激活函数，神经网络可以被简化为线性回归模型。激活函数必须是可微的。目前最流行的激活函数包括sigmoid、tanh、ReLU、Maxout和Swish。下面是它们之间的比较：

1. sigmoid：\(f(x)=\frac{1}{1+e^{-x}}\)。使用广泛，但存在梯度消失问题，这在网络较深时更显著。另一个问题是它不是以0为中心的，这会导致反向传播时权重要么全正要么全负，呈现zigzag状态使得优化困难。Softmax和sigmod类似，但sigmoid通常应用于二元分类，而softmax用于多分类。此外，在构建网络时，sigmoid用作激活函数，而softmax通常用在输出层。
2. tanh：\(f(x)=\frac{1-e^{-2x}}{1+e^{-2x}}\)。它的值是以0为中心的，它与sigmoid类似但导数更陡峭。tanh比sigmoid略有效，但同样面临梯度消失问题。
3. ReLU：\(f(x)=\max(0, x)\)。是使用最广的激活函数，同时也有许多变体(leaky ReLU，PReLU，EIU和SeLU)。ReLU计算简单，而且能够解决梯度消失问题，但同样面临两个主要问题：1）它的范围是从零到无限，这意味着它可以炸裂激活(blow up the activation)；2）负半轴导致的稀疏性。尽管如此，ReLU兼顾了简易性和高效性，通常可做为默认的激活函数。如果发生了梯度消失问题，可以使用leaky ReLU替换。
4. Maxout：\(f_i(x)=\max z_{ij}, z_{ij}=x^T W_{\dots ij}+b_{ij}\)。它是ReLU和leaky ReLU的泛化，实际上它也可以看作一层神经网络。Maxout是一个可学习的激活函数，解决了ReLU所有的问题，通常与dropout搭配使用，但也导致参数量增加。
5. Swish：\(f(x)=x \cdot \ sigmoid(x)\)。它计算简单，和ReLU的形状类似，而且是平滑曲线。但目前来看Swish仍然没有ReLU流行。
   

Hyper-Parameter Optimization: A Review of Algorithms and Applications

标签：因此   优化算法   很多   好的   物体检测   spro   alt   网络   ISE   

原文地址：https://www.cnblogs.com/weilonghu/p/12515991.html