标签:img 概率 归并 font div 分解 ret and template
快速排序的描述
与归并排序一样,快速排序也使用了分治思想。具体步骤:
分解:数组 A[p...r] 被划分为两个子数组(可能为空) A[p...q-1] 和 A[q+1...r] ,使得 A[p...q-1] 中的每一个元素都小于等于 A[q],而 A[q] 小于等于 A[q+1...r] 中的每个元素。
解决:通过递归调用快速排序,对子数组 A[p...q-1] 和 A[q+1...r] 进行排序。
合并:因为子数组都是原址排序的,所以不需要合并操作,数组 A[p...r] 已经有序。
代码实现
template<class T>
void QuickSort(T a[], int p, int r) {
if (p < r) {
int q = Partition(a, p, r);//分解
QuickSort(a, p, q - 1);
QuickSort(a, q + 1, r);
}
}
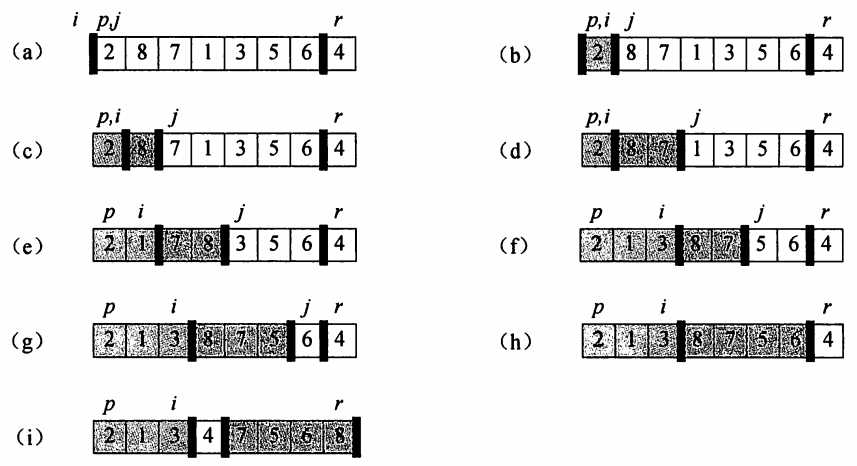
“分解”步骤代码
template<class T>
int Partition(T a[], int p, int r) {
T x = a[r];
int i = p - 1;
for (int j = p; j < r; j++) {
if (a[j] <= x) {
i++;
swap(a[i], a[j]);
}
}
i++;
swap(a[i], a[r]);
return i;
}
快速排序的性能
快速排序的运行时间依赖于分解是否平衡。如果分解是平衡的,即两个子问题规模相近,那么快速排序算法性能与归并排序一样。如果分解是不平衡的,最坏情况为两个子问题分别包含了 n-1 个元素和 0 个元素,那么快速排序的性能就接近于插入排序了。而平衡与否又依赖于用于划分的元素,为了降低最坏情况发生的概率,可以随机选取用于划分的元素。
代码实现
template<class T>
int RandomizedPartition(T a[], int p, int r) {
int i = ((double)rand() / RAND_MAX)*(r - p) + r;
swap(a[i], a[r]);
return Partition(a, p, r);
}
template<class T>
void QuickSort(T a[], int p, int r) {
if (p < r) {
int q = RandomizedPartition(a, p, r);
QuickSort(a, p, q - 1);
QuickSort(a, q + 1, r);
}
}

标签:img 概率 归并 font div 分解 ret and template
原文地址:https://www.cnblogs.com/bjxqmy/p/12528029.html