标签：bit += 一个 小数 遍历 最大值 单位 单源最短路 答案
图论难点：问题的转化和抽象（可看成特殊的某一类DP）
图论与DP的联系：
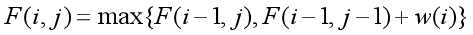
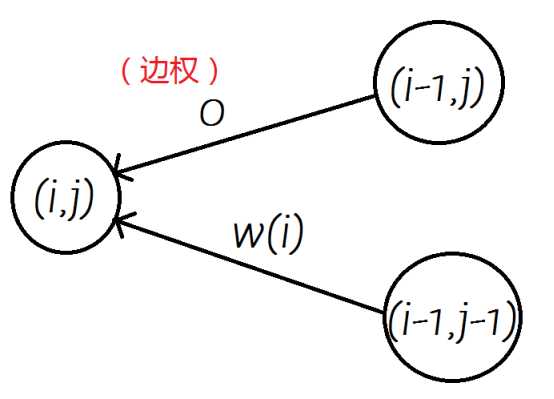
DP问题（从集合角度分析最优化问题）可以看成从F(0,0)、F(0,1)、F(1,2)......F(0,m)到F(n,m)的最长路。因此DP问题可以转化为拓扑图（一般DP问题的状态间无环）上的最短（长）路。
当DP依赖关系不具有拓扑序时（即存在环时），可以将其转化为最短路，也可以用高斯消元。
//TLE的原因常常是没有memsert
//st数组在不同算法中的用法：
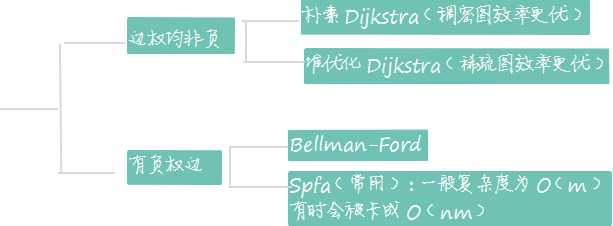
单源最短路的建图方式
AcWing 1129. 热浪
//单源最短路模型。朴素或堆优化Dijkstra、spfa皆可
AcWing 1128. 信使
//数据范围较小，Floyd算法直接处理
//核心：对于每个点来说，它接收到信的时间，等于它到指挥部 的最短距离。
//跑完最短路之后找出所有最短路中的最大值，若为正无穷则说 明该点与起点不连通，输出“-1”即可
//注意预处理时d[i][i]=0。
AcWing 1127. 香甜的黄油
//多源汇最短路问题（可用堆优化Dijkstra或Spfa）
//分析数据范围得知，Floyd算法会超时.所以可以枚举每一个点作为起点时的花费
AcWing 1126. 最小花费
//注意扣除手续费的计算：
w[i]=1-手续费i （0<w[i]<1）
100=d[A]*w[1]*w[2]*w[3]*w[4]......
所以为使d[A]最小,应使w[1]*w[2]*w[3]*w[4]......最大。
//令S=w[1]*w[2]*w[3]*w[4]......：
logS=log(w[1]*w[2]*w[3]*w[4]......)
=logw[1]+logw[2]+logw[3]+logw[4]......
因为0<w[i]<1，所以logw[i]<0，logS<0，-logS>0。那么，为使S最大，logS就应最大，-logS就应最小。其中，-logS可以看成是-logw[i]的和。
所以本题就可以转化成一个最短路问题，故可以用Dijkstra或spfa求解。代码可以直接用乘法来实现三角不等式，上述只是为了说明本题运用Dijkstra或spfa的正确性。
AcWing 920. 最优乘车
//sstream读入小技巧（原题未告知一行读入多少数）：
//注意这道题的特殊性：要求的是换乘次数最少的路线，而非最短路。可以将问题转化，在处于同一路线上的站点之间连一条权值为1的边，然后用经典最短路模型处理。因为所有的边权都是1,所以可以直接写BFS。
AcWing 903. 昂贵的聘礼
//tap：建立虚拟源点（标为0号点），表示直接买的价格，此时应注意一共有n+1个点。
//本题需要考虑等级限制：因为等级和等级限制都不超过100，所以可以枚举等级区间，在这个区间内进行Dijkstra，时间复杂度不超过100w。
单源最短路的综合应用
AcWing 1135. 新年好
//最短路+DFS 6*O（m）+5！
//当一个数组作为函数的形参被传入时，sizeof函数就无法正常工作，会RE。
AcWing 340. 通信线路
//最短路+二分
//定义在[0,1000001]这个区间中的性质如下：
对于区间中的某一个点，求出从1走到N，最少经过的长度大于x的边的数量是否小于等于k。
//求出从1到N最少经过几条长度大于x的边：
可以将所有的边分类：如果边长大于x，则边权看成1，否则边权是0。可以用双端队列BFS来求从1到N的最短路。
AcWing 342. 道路与航线
//这道题的路径有两种，一种是边权非负的双向边(道路)，一种是边权可正可负且无环的单向边(航线)。
//本题spfa会被卡。
//航线一定在不同的道路连通块之间，将每一个连通块看成一个点。具体实现方式：
1．先输入所有双向道路，然后DFS出所有连通块，计算两个数组：id[]存储每个点属于哪个连通块；vector<int> block[]存储每个连通块里有哪些点
2．输出所有航线，同时统计出每个联通块的入度
3．按照拓扑序依次处理每个连通块。先将所有入读为0的连通块的编号加入队列中
4．每次从队头取出一个连通块的编号bid
5．将该block[bid]中所有点加入堆中，然后对堆中所有点跑dijkstra算法
6．每次取出堆中距离最小的点ver
7．然后遍历ver的所有邻点j。如果id[ver]==id[j]，那么如果j能被更新，则将j插入堆中；如果id[ver]!=id[j]，则将id[j]这个连通块的入度减一，如果减成0了，则将其插入拓扑排序的队列中。
//体现单源最短路：
memset(dist,0x3f,sizeof dist);
dist[S]=0;
AcWing 341. 最优贸易
//最短路算法和DP的结合(本质上DP和最短路算法是有很大交集的，绝大部分DP都可以被看成是拓扑图上的最短路或最长路问题.)。采用类似于DP的思想，把所有从1到n的路径看成一个集合，进行子集的划分。
//假设S1,S2…St都可以走到第K个点.那么：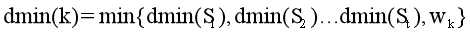
。dmax同理。
//DP问题所说的“无后效性”即转化为一个表示状态的图时,图上是不存在环的，但是这个问题中存在。因此可以用最短路算法处理上面的类DP问题。
//用spfa正确性：
for(迭代n-1次)
for(循环边)用三角不等式更新
Dijkstra算法中，每个点只出队一次，但是在本题中一个点可以被更新多次，所以Dijkstra算法不适用于这道题。
//从1到k买入的最小值dmin[k]
从k到n卖出的最大值dmax[k]
答案即max(dmax[k]-dmin[k])
单源最短路的扩展应用
AcWing 1137. 选择最佳线路
//可以建反向边，求出从终点到每个起点的最短路的最小值
原问题：从每个起点出发，到达终点的所有路径的最小值。
加上虚拟源点之后的问题：从虚拟源点出发，到达终点的所有路线的距离的最小值。将原问题转化成了单源最短路问题。
AcWing 1131. 拯救大兵瑞恩
//应用拆点的思想。最短路中需要拆点,分层的题目.一般都可以用DP的方式先考虑。因为有钥匙等因素的影响，因此f(i,j)并不能只用两维就表示出到点(i,j)的最短距离。仿照DP的思路，我们可以再加一维。
//但是这道题并不能按照DP的方式来写，因为一般能够用DP方式写的题目都需要保证在计算某个状态之前，所有能够更新它的状态都已经被更新了，即其状态与状态之间满足拓扑序。但是这道题某些点之间是可以相互到达的，因此存在环。所以还是要用最短路的方式来写。
//将二维变成一维：f(x,y,state)的前两维可以压缩成一维
//动态规划
一、状态表示：d(x,y,state)
1．集合：所有从起点走到(x,y)这个格子，且当前已经拥有的钥匙是state的所有路线的集合。
2．属性：最短距离
二、状态计算
1．(x,y)这里有一些钥匙，那么可以直接将所有钥匙拿起：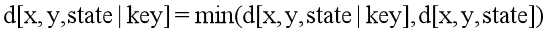
2．向上下左右四个方向走。
（1）没有门和墙
（2）有门，且有匹配的钥匙，之后走到了(a,b)：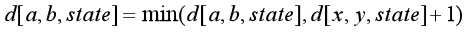
//状态间存在环形依赖，因此可以将DP转化成图论问题(BFS)
//Taps:
1．用一维数字表示二维位置
2．所有边权都是0或1，因此可以用双端队列，保证时间复杂度是线性的。
AcWing 1134. 最短路计数
//求方案数
//最短路树（拓扑图）上保证不存在边权为0的环，否则答案的方案数则为正无穷。
//本题用BFS或Dijkstra做没有问题，但是不能用spfa
//求方案数时如果有负权边，则先用spfa求一遍最短路，再循环遍历每一条边，若该边满足三角不等式，则加入最短路树中，最后将最短路树建好，再由拓扑序求最短路树上的方案数。
AcWing 383. 观光
//最短路径的条数
次短路径：如果存在比最短路径长度恰好多1的路径，则再把这样的路径条数加上
d[i,0]表示从1到i的最短路径 cnt[i,0]
d[i,1]表示从1到i的次短路径 cnt[i,1]
Floyd算法（兼具DP和图论的性质）
1．多源多汇最短路：可在的时间复杂度之内求出任意两点间的最短路
2．传递闭包：将所有可以间接到达的点连上直接到达的边
如果存在i->j这条边，则g[i,j]=1
如果不存在i->j这条边，则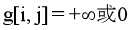
(1) 初始化：d[i,j]=g[i,j]
(2) for(k)
for(i)
for(j)
if(d[i,k]&&d[k,j])
d[i,j]=1;
3．找最小环
4．恰好经过k条边的最短路（倍增思想）
//Floyd和Bellman-Ford、spfa算法都是基于DP
Dijkstra基于贪心
//动态规划
一、状态表示
d[k,i,j]表示从i到j只经过1~k的话，最短路径是多少
1．集合：所有从i出发，最终走到j，且中间只经过节点编号不超过k的所有路径。
2．属性：路径长度的最小值
二、状态计算
1．所有不含节点k的路径
最小值为d[k-1,i,j]
2．所有包含节点k的路径
最小值为d[k-1,i,k]+d[k-1,k,j]
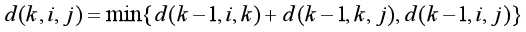
去掉第一维后：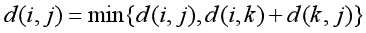
下面来证明循环当中是否可以去掉第一维：
特殊情况：当k=j时，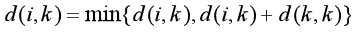
由于经过预处理，d(k,k)=0，所以d(i,k)=d(i,k)。说明在循环一轮后，d(k,i,k)仍然等于d(k-1,i,k)。同理得d(k,k,j)=d(k-1,k,j)。所以在循环中可以去掉第一维。
AcWing 1125. 牛的旅行
//牧区：节点
牧场：连通块
//具体思路：
(1) 用floyd算法求出任意两点之间的最短距离
(2) 求maxd[i]，表示和i连通的且距离i最远的点的距离
(3) 情况1：答案为所有maxd[i]的最大值
情况2：枚举在哪两个点之间连边，需要满足d[i,j]=INF。答案为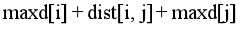
//本题数据较大，INF最好定义为1e20
AcWing 343. 排序
//假定如果A<B，则d(A,B)=1
1．矛盾：d(i,i)=1
2．唯一确定：当i≠j时，d(i,j)、d(j,i)中必有一个是1
3．顺序不唯一
//改良 将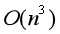
变成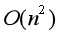
：
AcWing 344. 观光之旅
//集合：按照环上编号最大的点分类
如果d(i,j)=d(i,k)+d(k,j)，则k为i->j中编号最大的点
AcWing 345. 牛站
//d[k,i,j]表示从i到j，恰好经过k条边的最短路径
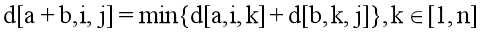
（本题中可以存在负环）
//满足结合律，那么就可以用倍增（快速幂）的思想处理这道。由d(2,i,j)得到d(4,i,j)，再得到d(8,i,j)
因此时间复杂度可优化为
//因为实际用到的点数远小于总的点数，所以可以把点的编号离散化一遍，降低时间复杂度。
最小生成树（无向边）
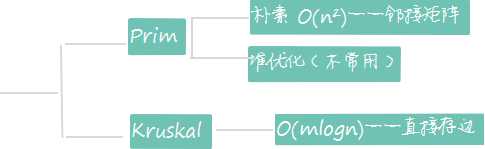
当前与外界直接相连的权值最小的一条边。这条边一定可以出现在最优解中。
如何证明当前这条边一定可以被选？
假设不选当前边，最终得到了一棵树。然后将这条边加上，那么必然会出现一个环，在这个环上，一定可以找出一条长度不小于当前边的边，那么把当前边替换上去，结果一定不会变差。
AcWing 1140. 最短网络
AcWing 1141. 局域网
//相当于在这个图的每个连通块内，求一棵最小生成树。相当于求原图的“最小生成森林”。
//做Kruskal算法：
如果a和b不连通，那么就将当前边加到最小生成树中去。
//可以用Prim算法时一定可以用Kruskal算法，但用Kruskal算法时不一定可以用Prim算法（例如本题）
AcWing 1142. 繁忙的都市
//普通的最小生成树：所有的边权之和最小
本题中的最小生成树：最大的边权最小
//做法：Kruskal
如果a和b已经连通，那么直接pass
如果a和b不连通，那么就将当前边选出来
AcWing 1143. 联络员
//读题->分析模型->算法->代码
1．将所有必选边加到并查集中
2．将所有非必选边从小到大排序
3．从小到大依次枚举每一条非必选边，a，b，w
如果a和b已经连通，直接pass
如果a和b不连通，那么就将当前边选上
//Kruskal算法：可以只实现前一半，也可以在已经有边的前提下继续做后一半
AcWing 1144. 连接格点
//注意！这不是一个最小生成树问题：n个点，m条边，边权可正可负，求将所有点连通的最小边权和是多少？
//O(klogk)->O(k)
//将二维变成一维
//容易冲突的变量名：y1，next，prev，hash
//为了省去排序的时间，先将纵向边（权值为1）加入，再将横向边（权值为2）加入
最小生成树的扩展应用
定理：
任意一棵最小生成树一定可以包含无向图中权值最小的边
证明：
反证法。假设无向图G=(V,E)存在一棵最小生成树不包含权值最小的边。设e=(x,y,z)是无向图中权值最小的边。把e添加到树中，e会和树上从x到y的路径一起构成一个环，并且环上其他边的权值都比z大。因此，用e代替环上的其他任意一条边，会形成一棵权值和更小的生成树，与假设矛盾。故假设不成立，原命题成立。
推论：
给定一张无向图G=(V,E),n=|V|,m=|E|。从E中选出k<n-1条边构成G的加一个生成森林。若再从剩余的m-k条边中选n-1-k条添加到生成森林中，使其成为G的生成树，并且选出的边的权值之和最小，则该生成树一定包含这m-k条边中连接生成森林的两个不连通节点的权值最小的边。
//以上来自《算法竞赛 进阶指南》
AcWing 1146. 新的开始
//建立一个“超级发电站”，将所有矿井与其都连上边
AcWing 1145. 北极通讯网络
//找一个最小的d值，使得将所有权值大于d的边删去之后，整个图形的连通块的个数不超过k。
//Kruskal算法：假设当前已经循环完第i条边。已经求出了由前i条边构成的连通块。
//可以用DFS/BFS+二分，但用并查集的话则无需二分
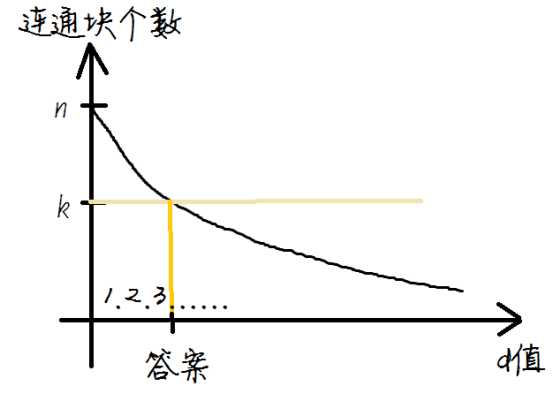
AcWing 346. 走廊泼水节
//对于两个连通块：
这样才能保证图的唯一最小生成树仍是原树。
AcWing 1148. 秘密的牛奶运输
//次小生成树
定义：给一个带权的图，把图的所以生成树按权值从小到大排序，第二小的称为次小生成树。
//非严格次小生成树的边权可以和最小生成树相等，而严格次小生成树则不可以。
定理：对于一张无向图，如果存在最小生成树和（严格）次小生成树，那么对于人格一棵最小生成树，都存在一棵（严格）次小生成树，使得这两棵树只有一条边不同。
方法1：先求最小生成树，再枚举删去最小生成树中的边求解。时间复杂度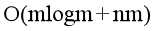
方法2：先求最小生成树，然后依次枚举非树边，然后将该边加入树中，同时从树中去掉一条边，使得最终的图仍是一棵树。则一定可以求出次小生成树。
定理：次小生成树一定在最小生成树的邻集中。
//以上来自《信息学奥赛一本通·提高篇》
要使得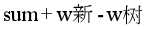
最小，就要使最大。可以枚举n个点，以每一个点为树根，复杂度预处理出每个点到其他所有点的路径上的最大边权。所以时间复杂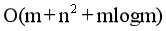
//也可以用树链剖分进行预处理
1．求最小生成树，标记每条边是树边，还是非树边；同时把最小生成树建立出来。
2．预处理任意两点间的边权最大值dist[a][b]
3．依次枚举所有非树边，求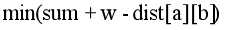
，满足w>dist[a][b]。
//注意：在求严格次小生成树时，不能只预处理两点之间最大的树边，因为当最大树边和当前枚举的非树边长度相同时，就不能替换了，但此时却可以替换长度次大的树边。因此还需同时预处理出长度次大的树边。
负环
01分数规划
求负环的常用方法，基于spfa：（基于抽屉原理）
将所有点加入队列中，并初始化dist[i]=0。此时可以看成由虚拟源点向所有点都连了一条边，不影响负环的判断。又因为无论dist数组初始化成0还是0x3f3f3f3f，有负环存在都会逐渐减为负无穷，所以初始化成任意值皆可。也没必要memset
当所有点的入队次数超过2n时，我们就认为图中与很大可能是存在负环的。
AcWing 904. 虫洞
AcWing 361. 观光奶牛
//使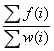
最大，即01分数规划问题。
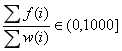，可用二分。
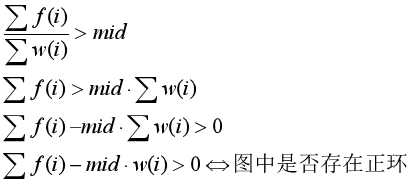
将边权重定义为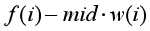
，判断是否存在正环不一定要把边权取负，可以在spfa中改变判断符号，变成求最长路。
//保留两位小数，二分时>1e-4即可
同理，若保留三位小数，则>1e-5
AcWing 1165. 单词环
//建图：
以每个单词的前两个字母和后两个字母为节点，以单词的长度为边，最多建立676个点、10?条边
//同样还是01分数规划问题，解法同上题
//优化：在循环时计数，当循环次数cnt>2*n（n为点数）时就可以直接认为存在正环。将队列换成栈也可以。（但在普通题目中无需将队列换成栈，因为栈的效率极低）
差分约束
(1) 求不等式组的可行解
源点需要满足的条件：从源点出发，一定可以走到所有的边。
步骤：
结果：
//最短路：所有从1->i的路径的最小值
最长路：所有从1->i的路径的最大值
(2) 如何求最大值或最小值，这里的最值指的是每个变量的最值
结论：
如果求的是最小值，则应该求最长路；如果求的是最大值，则应该求最短路。
以求xi的最大值为例：所有从xi出发，构成的不等式链xi<=xj+c1<=xk+c2+c1<=...<=c1+c2+...+ck所计算出的上界，最终xi的最大值等于所有上界的最小值。
同理，若是求最大值，则是求所有下界的最大值。
问题：
如何转化xi<=c，其中c是一个常数，这类的不等式
方法：
建立一个超级源点，0，然后建立0->xi，长度是c的边即可
AcWing 1169. 糖果
//最小值则求最长路
相对关系：
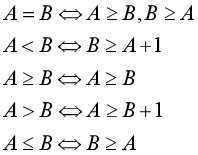
绝对关系：
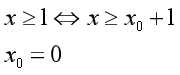
//无解情况：是否存在正环
//边数组大小开三倍N（最坏情况下都是A=B，需要建双向边，另外每个点都要和超级源点连一条边）
//优化：如果用队列会TLE几个数据点，所以将队列替换成栈
AcWing 362. 区间
//贪心或差分约束
首先将所有ai变成ai+1，bi变成bi+1，这样数据范围就变成了[1~50001]，为了将0腾出来建立超级源点
//最小值则求最长路（dist数组初始化为-0x3f）
//前缀和思想：Si表示1~i中被选出的数的个数。
//注意：
AcWing 1170. 排队布局
//最大值则求最短路
建立虚拟源点使得，即从虚拟源点向i号点连了一条边。但在实际操作中无需真的建立出虚拟源点，将所有点都入队即可。
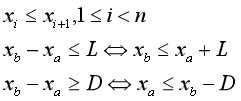
//无解情况：判断是否存在负环
//由于题目给定的是相对关系，所以可以令X1=0，那么题目所求的Xn-X1就是Xn，只要求出X1到所有点的最短路，如果Xn的值为正无穷，则说明 1 号奶牛和 N 号奶牛间的距离可以任意大，否则1 号奶牛和 N 号奶牛间可能的最大距离即Xn。
//本题需要进行两次spfa，对于第一问，需将所有点都入队，即spfa(n)；对于第二问，只需求出X1到其他点的最短路，即spfa(1)。 //注意每次spfa前都要初始化：
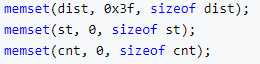
cnt数组记录当前路径的边数，即用来判断是否存在负环。
AcWing 393. 雇佣收银员
//最小值则最长路
//num[i]表示i时刻来的人数
X[i]表示最终从num[i]中挑出来的人数
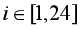，也是为了将0腾出来建立超级源点
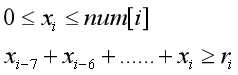
//前缀和思想：令Si为Xi的前i项和，则
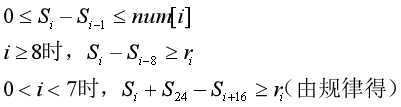
即
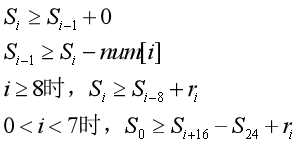
由于在最后一个式子中有三个变量，所以我们可以直接从小到大在0~1000内枚举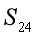
，如果找到符合条件的就直接输出，若循环结束仍未找到则说明无解。
//在枚举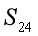
的过程中，为了体现
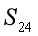是个定值，即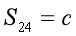
最近公共祖先
fa[i,j]表示从i开始，向上走2^j步所能走到的节点。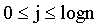
depth[i]表示深度
//哨兵：如果从i开始跳2^j步会跳过根节点，那么fa[i,j]=0。 depth[o]=0
//步骤：（二进制拼凑法）
(1) 先将两个点跳到同一层
(2) 让两个点同时往上跳，一直跳到它们的最近公共祖先的下一层。
预处理 O(nlogn) //广搜，不会爆栈
查询O(logn)
//j=0，f(i,j)=i的父节点
j>0，f(i,j)=f(f(i,j-1),j-1)
//本质上是对向上标记法的优化
在深度优先遍历时，将所有点分成三大类：
1) 已经遍历过，且回溯过的点
2) 正在搜索的分支
3) 还未搜索到的点
AcWing 1172. 祖孙询问
//倍增求lca
AcWing 1171. 距离
//两点之间的最短距离：d(x)+d(y)-2*d(lca(x,y))
//预处理出每个节点到根节点的距离d(i)
//用vector<PII>来存询问，first存查询的另外一个点，second存查询编号
AcWing 356. 次小生成树
//注意要用long long，会爆int
//思路和AcWing 1148. 秘密的牛奶运输相似
//d1[i,j]表示i->j路径上的最大边
d2[i,j]表示i->j路径上的次大边
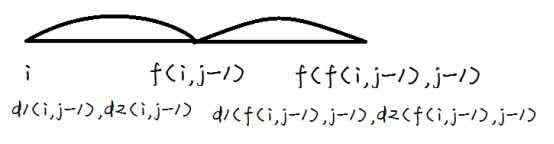
AcWing 352. 闇の連鎖
//树上差分
给从x到y的路径上的所有边都加上c：
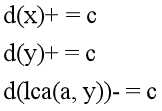
//最后枚举每棵子树：
有向图的强连通分量
对于一个有向图，连通分量：对于分量重任意两点u，v，必然可以从u走到v，且从v走到u。
有向图通过缩点（将所有连通分量缩成一个点）变成有向无环图（DAG），即拓扑图，便于求最短（或最长）路、递推。时间复杂度为O(n+m)。
DFS（树枝边、前向边：指向某个子孙、后向边：指向某个祖宗、横叉边）
情况1：存在后向边指向祖先节点
情况2：先走到横叉边，横叉边再走到祖先
Tarjan算法求强连通分量（SCC）
对每个点定义两个时间戳：
dfn[u]表示遍历到u的时间戳
low[u]从u开始走，所能遍历到的最小时间戳是什么。
u是其所在的强连通分量的最高点，等价于dfn[u]==low[u]
//栈中放当前强联通分量中还没有搜完的所有点
for(i=1;i<=n;i++)
for(i的所有邻点j)
if(i与j不在同一个SCC中)
加一条新边 id(i)->id(j)
//连通分量编号递减的顺序一定是拓扑序
AcWing 1174. 受欢迎的牛
//先缩点，再在拓扑图里找出出度为零的点。（如果有两个或以上这样的点，本题答案即为0）答案即这个点所代表的强连通分量中的点数。
AcWing 367. 学校网络
//设缩点后有P个起点，Q个终点
//第一问即P
//第二问为max(P,Q)
假设|P|≤|Q|
1) |P|==1 ans=|Q|
2) |P|>1 |Q|≥|P|>1
必能找到两个不同的起点到达不同的终点，设这两个起点分别为p1、p2，终点分别为q1、q2。
//反证：如果找不到这样的两个点，说明所有起点都到达同一个终点q1。但|Q|>|P|，所以必然有q2是来自其中一个起点，得出矛盾。
此时给q1、p2连一条边，则|P’|=|P|-1，|Q’|=|Q|-1。连|P|-1次这样的边，使得|P|=1，那么此时总共连的边数为|Q|-(|P|-1)+|P|-1，即|Q|。
//第二问注意特判：如果只有一个强连通分量，则答案为0
AcWing 1175. 最大半连通子图
//导出子图：从原图中选出一些点，再把所有跟这些点相关的边都选出来（如果两点间有多条边，则应将这些边全部选出）。
//第一问：求拓扑图的最长链
//第二问：求最长链的方案数 DP
设f(i)为表示到i这个点的最长链的长度，g(i)表示到到i这个点的最长链的方案数，s(i)表示i这个强连通分量中的点数。
如果可以从j->i：
1．若f(j)+s(i)>f(i)，则f(I)=f(j)+s(i)，且g(i)=g(j)
2．若f(j)+s(i)==f(i)，则g(i)+=g(j)
//因为连通分量编号递减的顺序一定是拓扑序，所以无需再次建图，只要按照该顺序DP即可。
AcWing 368. 银河
//本题正解：Tarjan算法（稳定，时间复杂度可达线性）
//本题可以用01分数规划，思路类似AcWing 1169. 糖果 ，将队列换成栈，仍有超时的风险。
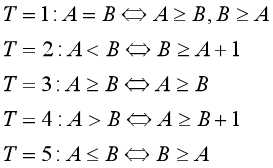
另外还有两个条件：
1．必须有绝对值
2．超级源点
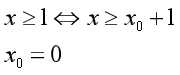
//本题的特殊性：
边权都为正，因此在判断是否存在正环时，只要在某一个强连通分量中有某一条边的权值大于0，就形成了一个正环（因为强联通分量中的任意两点都互相连通）。所以强连通分量中的所有边的权值都要为0，即所有点最终的距离都相等。因此题目变成了在拓扑图上，所有点到起点的最长距离。
//建立了超级源点后，就可以直接Tarjan(o)。
//本题需要用long long
无向图的双连通分量（也叫重连通分量）
边双连通分量e-DCC：极大的不包含桥的连通块
//桥：删去桥原图不连通
//性质1：不管删掉哪条边，该图仍然连通
性质2：任意两点之间都存在两条不相交的路径
点双连通分量v-DCC：极大的不包含割点的连通块
//割点：删去割点原图不连通
//每一个割点都至少属于两个连通分量
//两个割点之间的边不一定是桥，桥的两个端点也不一定是割点
一个点双连通分量不一定是一个边双连通分量，同样地，一个边双连通分量也不一定是一个点双连通分量
边双连通分量：dfn(x)、low(x)
如何找到桥：
如何找到所有边的双连通分量：
如何求割点：low(y)≥dfn(i)
(1) 如果x不是根节点，那么x是割点
(2) x是根节点，至少有两个子节点yi满足low(yi)≥dfn(i)
如何求点双连通分量：
1) 统计连通块个数 cnt
2) 枚举从哪个块删，再枚举删除哪个点
AcWing 395. 冗余路径
//两条路径没有一条重合的道路
//给定一个无向连通图，问最少加几条边，可以将其变成一个边双连通分量。
//将所有边双连通分量缩点，原图变成了一棵树，再将所有叶子节点连接起来。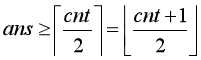
（cnt为叶子节点的数量）
AcWing 1183. 电力
//求割点 stack
//多组数据记得memset(dfn,0,sizeof dfn)
//孤立点也是双联通分量
AcWing 396. 矿场搭建
//给定一个无向图，问最少在几个点上设置出口，可以使得不管哪个点坍塌，其余所有点都可以与某个出口连通。
1) 无割点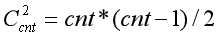 
2) 有割点
1．每个割点单独作为一个点
2．从每个v-DCC向其所包含的每个割点连边
欧拉回路和欧拉路径
哥尼斯堡七桥问题（一笔画）
(1) 存在欧拉路径的充分必要条件：度数为奇数的点只能有0或2个。
(2) 存在欧拉回路的充分必要条件：度数为奇数的点只能有0个。
(1) 存在欧拉路径的充分必要条件：要么所有点的出度均等于入度；要么除了两个点以外，其余所有点的出度等于入度，剩余的两个点：一个满足出度比入度多1（起点），另一个满足入度比出度多1（终点）。
(2) 存在欧拉回路的充分必要条件：所有点的出度均等于入度。
实现方式：dfs，在dfs的最后将当前遍历的节点加入队列中
注意：用边判重，时间复杂度可能会很高。可以在走过一条边之后就将这条边删去。在无向图中，由于建了双向边，两条边都要删掉。双向边的编号为(1,2) (3,4) (5,6)......
AcWing 1123. 铲雪车
//由于每个点的入度和出度都相等，从起点可以到任意一条街道，显然本题就是一个欧拉回路。只要将所有街道的长度之和乘2，再除以铲雪车的速度即可。
//注意答案输出的单位转化
//本题乍一看是一道图论题，但实际上通过分析题目不难得出欧拉回路的结论。
AcWing 1184. 欧拉回路
//如何判断无解：
(1) 所有点的度数必须是奇数
(2) 所有边连通
(1) 所有点的入度等于出度
(2) 所有边连通
AcWing 1124. 骑马修栅栏
//保证dfs中for循环里u的所有出边都按照从小到大的顺序，这样输出的答案就会是字典序最小的。
AcWing 1185. 单词游戏
//以字母为点（26个点），以单词为边
判断有向图是否存在欧拉路径：
拓扑排序
拓扑图=有向无环图
将所有入度为0的点入队
对于任意一个点，其前驱点的个数都是有限的
AcWing 1191. 家谱树
//每输入一个孩子，就使孩子的入度++
//拓扑排序模板
AcWing 1192. 奖金
//差分约束求最长路
1) 边权无限制 spfa O(nm)
2) 边权非负 tarjan O(n+m)
3) 边权>0 拓扑排序 O(n+m)
//用拓扑排序来做差分约束问题。每个点都最小，使得总和最小
AcWing 164. 可达性统计
//DP：
f(i)：所有能从i到达的点的集合
集合用长度为n的二进制串表示（例如1011001......），并使用bitset函数
AcWing 456. 车站分级
//暴力建图会超时
//告诉我们很多个a>b，要求最小的等级，即从b->a建立边权为1的边（很裸的查分约束问题）
1．拓扑排序
2．虚拟源点：将n^2的复杂度变成了线性
//若要连接两个集合，可在集合之间建立一个虚拟源点，从左边的集合中的每一个点向虚拟源点建立一条边权为0的边，再从虚拟源点向右边集合中的每一个点建立一条边权为1的边
---------------------------------------------------->
在最后，感谢Gold_stein（xym）同学提供了自己的笔记供我参考 Thanks?(?ω?)?
标签：bit += 一个 小数 遍历 最大值 单位 单源最短路 答案
原文地址：https://www.cnblogs.com/ljy-endl/p/12549209.html
