标签:重叠 噪声 listen 基于 pen from 画图 所有权 show
(1)思想
(2)例:
如下图所示,如何判断绿色圆应该属于哪一类,是属于红色三角形还是属于蓝色四方形?
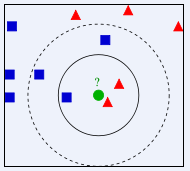
由于KNN最邻近分类算法在分类决策时只依据最邻近的一个或者几个样本的类别来决定待分类样本所属的类别,而不是靠判别类域的方法来确定所属类别的,因此对于类域的交叉或重叠较多的待分样本集来说,KNN方法较其他方法更为适合
KNN算法即可以应用于分类算法中,也可以应用于回归算法中。
KNN算法的准确性很大程度上依赖于K值的选择
(1)为什么选择K值
(2)K值的选择过程

(1)欧几里得距离
使用欧几里得距离:欧几里得度量(euclidean metric)(也称欧氏距离)是一个通常采用的距离定义,指在m维空间中两个点之间的真实距离,或者向量的自然长度(即该点到原点的距离)
\(d(X,Y)=\sqrt{(x_1-y_1)^2+(x_2-y_2)^2+...+(x_n-y_n)^2}=\sqrt{\sum_{i=1}^n{(x_i-y_i)^2}}\)
(2)曼哈顿距离
定义曼哈顿距离的正式意义为L1-距离或城市区块距离,也就是在欧几里德空间的固定直角坐标系上两点所形成的线段对轴产生的投影的距离总和。
例如在平面上,坐标X(x1,x2)的与坐标Y(y1,y2)的曼哈顿距离为:
\(d(X,Y)=|x_1-y_1|+|x_2-y_2|\)
(1)KNN算法的不足
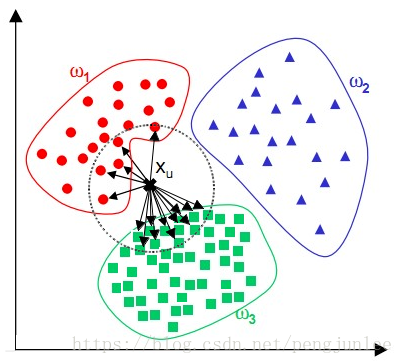
(2)加权方式
(3)具体算法
计算测试数据与各个训练数据之间的距离
按照距离的递增关系进行排序
选取距离最小的K个点
确定前K个点所在类别的出现频率
返回前K个点中出现频率最高的类别作为测试数据的预测分类
from sklearn.datasets import load_iris
from sklearn.model_selection import cross_val_score
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsClassifier
#读取鸢尾花数据集
iris = load_iris()
x = iris.data
y = iris.target
k_range = range(1, 31)
k_error = []
#循环,取k=1到k=31,查看误差效果
for k in k_range:
knn = KNeighborsClassifier(n_neighbors=k)
#cv参数决定数据集划分比例,这里是按照5:1划分训练集和测试集
scores = cross_val_score(knn, x, y, cv=6, scoring=‘accuracy‘)
k_error.append(1 - scores.mean())
#画图,x轴为k值,y值为误差值
plt.plot(k_range, k_error)
plt.xlabel(‘Value of K for KNN‘)
plt.ylabel(‘Error‘)
plt.show()
标签:重叠 噪声 listen 基于 pen from 画图 所有权 show
原文地址:https://www.cnblogs.com/nishoushun/p/12630629.html