标签:动态 组成 多个 很多 搜索 效果 用两个 没有 使用
在对处理后的图像数据进行分析之前,图像分割是最重要的步骤之一。它的主要目标是将图像化分为与其中含有的真实世界的物体或区域有枪相关性的组成部分。
其中图像数据的不确定性是主要的分割问题之一,通常伴随着信息噪声。
按照主要特征可以将分割方法分为:
灰度阈值化是最简单的分割处理。很多物体或图像区域表征为不变的反射率或其表面光的吸收率,可以确定一个亮度常量——阈值,从而来分割物体和背景。
方法主要是依据对所有像素的函数值与阈值 T 比较,从而确定是物体像素 or 背景像素。应用举例如下图:
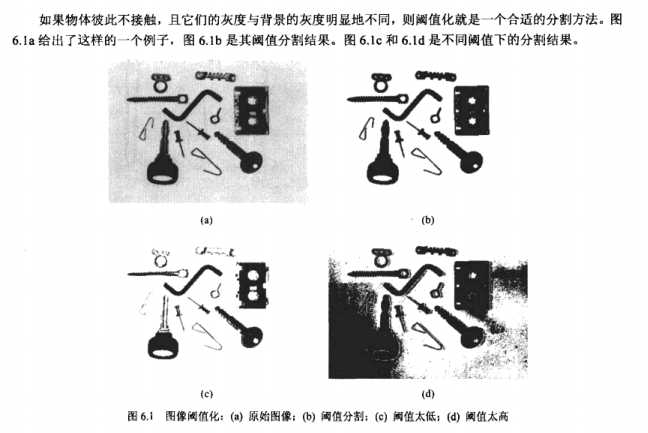
需要事先知道经过分割后的图像的某种性质,就可以简化阈值选择的任务,因为阈值可以确保该性质得以满足的条件来选择。
缺点:通常没有关于面积比率的先验信息。
二模态阈值检测算法通常首先寻找最大的局部极大值,然后取它们之间的极小值作为阈值,这种技术称为模式方法。
还有一些其他的阈值检测方法,例如:直方图凹度分析、熵方法、松弛法、多阈值方法等。
将图像的直方图用两个或更多个正态分布的概率密度函数来近似的方法,代表一种被称为最优阈值化的方法。这一方法在图像对比度条件变化很大的范围内性能良好。
将最优化和自适应阈值化结合起来的方法可应用与脑MR图像的分割。这种方法的局部子区域中计算局部直方图,以确定最优灰度分割函数。
许多实际的分割问题需要比单一谱段所含的更多的信息。例如,彩色图像的信息包含在三个谱段中,气象卫星图像可能具有更多的谱段。一种分割方法是在每个谱段中独立确定阈值,然后综合起来形成单一的分割图像。
例如,下图的算法步骤解释:

基于边缘的分割代表了一大类基于图像边缘信息的方法。基于边缘的分割依赖于由边缘检测算子找到的图像边缘,这些边缘表示除了图像在灰度、彩色、纹理等方面不连续的位置。
在分割处理中可获得的先验信息越多,能达到的分割效果越好。
在边缘图像中几乎没有0值像素,但是小的边缘值对应于由量化噪声、弱不规则照明引起的费显著的灰度变化。可以对边缘图像做简单的阈值化处理排除这些小的数值。这种方法是基于图像的边缘幅度由合适的阈值处理实现。
由于边缘图像阈值化方法得到边界受图像噪声的影响很大,经常会遗漏重要的部分。通过在它们相互邻域的上下文中考虑边缘的性质能够增加图像的品质。
所有的图像性质包括进一步的边缘存在性在内,都经过迭代评价而精确性提高,直至所有的边缘上下文完全清晰位置。这种评价是基于指定局部邻域内的边缘强度进行的,每个边缘的信度可能被增加 or 被减小。
如果区域的边界未知,单区域本身在图像中已经定义了,那么边界可以唯一地检测出来。算法如下:

还有一些其他的搜索方法,eg.基于图的边缘跟踪、作为动态规划的边缘跟踪、Hough变换、使用边界未知信息的边界检测等方法。
以区域的边界构造区域以及检测存在的区域的边界是容易做到的。但是,通过基于边缘的方法和由区域增长方法得到的分割,通常并不总是相同的。因此引入了基于区域的分割方法。
最自然的区域增长方法是原始图像数据上开始增长,每个像素表示一个区域。算法如下:

与区域归并相反,从将整个图像表示为单个区域开始,该区域一般不能满足条件\(H(R_i) = True,i=1,2,...S\)。
区域分裂方法一般使用与区域归并方法相似的准则,区别仅在于应用的方向上。
这种方法可以兼有分裂与合并两种方法的优点。分裂与归并方法在金字塔图像表示上进行,区域是方形的与合适的金字塔层元素对应。
算法如下图:

除以上之外,还有分水岭分割、区域增长后处理等方法。
标签:动态 组成 多个 很多 搜索 效果 用两个 没有 使用
原文地址:https://www.cnblogs.com/somedayLi/p/12650291.html