标签:查询 names ble ima 遍历 size 二叉查找树 lse i++
树上两点的最近公共祖先问题(LCA - Least Common Ancestors)
对于有根树T的两个结点u、v,最近公共祖先LCA(T,u,v)表示一个结点x,满足x是u和v的祖先且x的深度尽可能大。在这里,一个节点也可以是它自己的祖先。
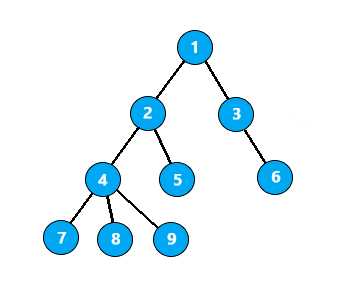
例如,如图,在以A为根的树上
节点 8 和 9 的LCA为 4
节点 8 和 5 的LCA为 2
节点 8 和 3 的LCA为 1
区别就在于是同时处理询问后输出还是边询问边输出
在线算法是读入一组询问,查询一次后紧接着输出一次
离线算法是读入全部的询问,在查询的过程中将所有询问全部处理,最后一起输出
如果给定的是一颗二叉查找树,那么每次询问就能从根节点开始,拿查询的两个数与节点的值进行对比。如果查询到两个数位于某个节点的两侧时,说明这个节点就是他们的LCA。这是特殊情况的特殊解法。
而LCA问题一般给定的不会是二叉树而是生成树。有可能会限制根节点,也有可能不会限制。在未限制根节点时,建图可以以任意一个节点作为根节点来建树。
常见在线算法为倍增法(待补)
常见离线算法为Tarjan算法(下文)
也可以选择将LCA问题转化成RMQ问题(求区间最值问题,待补)使用常用的ST算法求解
这个算法主要用到dfs与并查集
给每个节点置一个组别(并查集),如下图
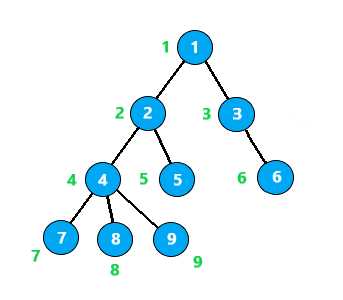
离线算法,记录下所有待查询的节点对
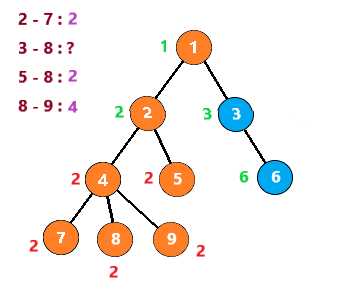
这里假设要查询的点对有 2 - 7 8 - 9 8 - 5 8 - 3
从根节点开始深搜,遍历所有子树
第一次,遇到节点2时,发现7与它有查询关系。但是7还没有被搜索到,所以不做处理
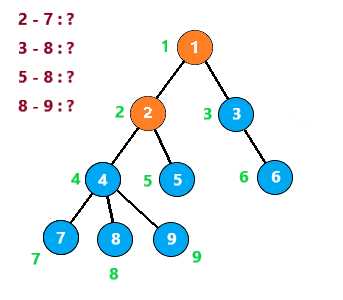
向下,到节点7时,发现2与他有查询关系。发现2已经被搜索过了,那么2与7的LCA就是此时2所在的集合,即2
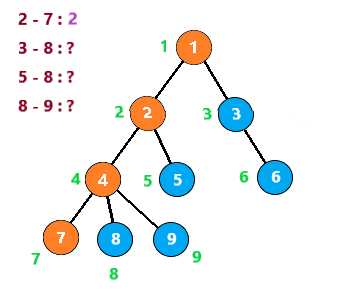
节点7之后没有子树,所以进行回溯
把节点7与节点7的所有子节点(无)组别置为节点7的父节点,然后继续搜索节点4的其他子树
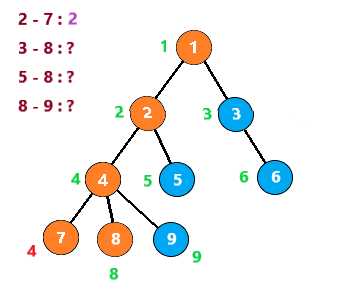
搜索到节点8,发现与它有查询关系的 3 5 9节点均没有被搜索过,故像上一步一样回溯后继续查询
接着查询节点9,发现8与它有查询关系且节点8已经被搜索过,所以8与9的LCA就是此时8所在集合,即4
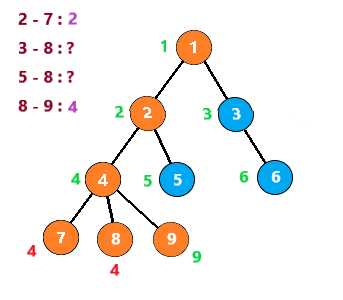
也就是说,当你搜索到一个节点 u ,发现节点 v 与它有查询关系且节点 v 已经被搜索过时,那么LCA(u,v)就是此时v所在的集合
按照这个思路继续下去,得到下列步骤
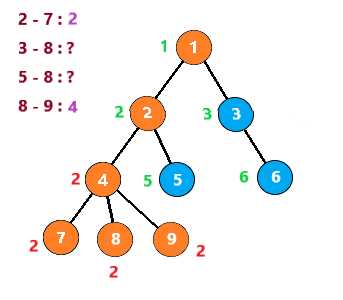
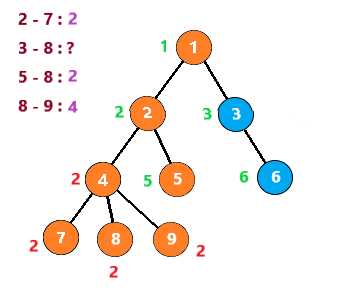
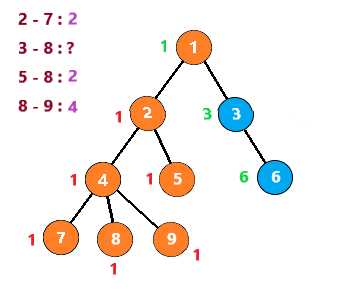
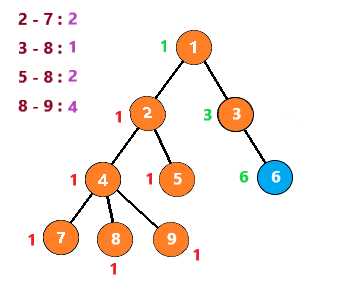
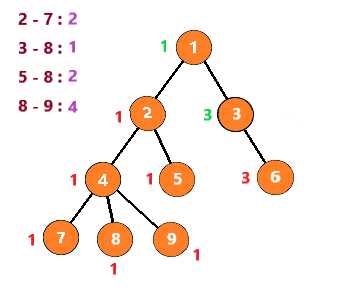
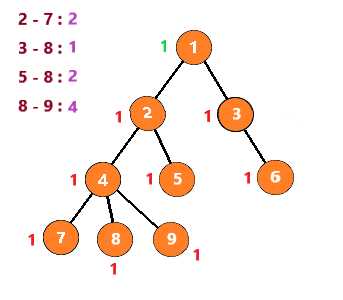
至此,整个图就搜索完了,时间复杂度为 O(节点个数n+查询数量m)
第一行给出三个数n m q,表示有n个节点,m条边,q次询问 (假设此时n,q<=10000)
接下来m行,每行两个数a b (1≤a,b≤n , a≠b),表示这两个节点之间存在一条边
接下来q行,每行两个数a b (1≤a,b≤n),询问LCA(a,b)
typedef pair<int,int> P;
const int MAXN=10050,MAXQ=10050;
bool vis[MAXN];
int ans[MAXQ],gp[MAXN];
vector<int> G[MAXN];//存图,G[i]存节点i的子节点编号
vector<P> ask[MAXN];//ask[i]的first存与i有查询关系的点编号,second存答案指向ask数组的位置
存图的时候我是让编号小的节点指向编号大的节点来处理搜索的先后顺序
因此存图只要存小编号指向大编号即可
以节点 1 为根节点开始搜索
void solve()
{
int n,m,q,a,b;
scanf("%d%d%d",&n,&m,&q);
for(int i=1;i<=n;i++)
{
gp[i]=i;
vis[i]=false;
}//并查集和vis数组的的初始化
for(int i=1;i<=m;i++)
{
scanf("%d%d",&a,&b);
if(a>b)
swap(a,b);
G[a].push_back(b);//小编号指向大编号
}
for(int i=1;i<=q;i++)
{
scanf("%d%d",&a,&b);
if(a==b)
ans[i]=a;//可能有些题目会出现这样的情况,此时答案直接指向自己即可,不用加入vector
else
{
ask[a].push_back(P(b,i));
ask[b].push_back(P(a,i));//因为一对点在搜索期间肯定会出现一次另一个点没有被搜索到的情况,所以给两个点都打上标记便于处理
}
}
tarjan(1);//从节点1开始搜索
for(int i=1;i<=q;i++)
printf("%d\n",ans[i]);
}
这里跟平常的一样,直接一句路径压缩递归来处理
int fnd(int p)
{
return p==gp[p]?p:(fnd(gp[p]));
}
当搜索到节点pos时,处理顺序为:先置访问标记为true,再处理答案,最后再去搜索pos的子树
void tarjan(int pos)
{
vis[pos]=true;//访问标记
int cnt=ask[pos].size();
for(int i=0;i<cnt;i++)//处理答案
{
if(vis[ask[pos][i].first])//如果first节点已经访问过,那么它此时所在的集合即LCA
ans[ask[pos][i].second]=fnd(gp[ask[pos][i].first]);//存答案,注意要进行一次对集合根节点的查询
}
cnt=G[pos].size();
for(int i=0;i<cnt;i++)//搜索子树
{
tarjan(G[pos][i]);
gp[G[pos][i]]=pos;//搜索完子树后,子节点的集合指向pos
}
}
9 8 4
1 2
1 3
2 4
2 5
3 6
4 7
4 8
4 9
2 7
3 8
5 8
8 9
2
1
2
4
#include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> P;
const int MAXN=10050,MAXQ=10050;
vector<int> G[MAXN];
bool vis[MAXN];
vector<P> ask[MAXN];
int ans[MAXQ],gp[MAXN];
int fnd(int p)
{
return p==gp[p]?p:(fnd(gp[p]));
}
void tarjan(int pos)
{
vis[pos]=true;
int cnt=ask[pos].size();
for(int i=0;i<cnt;i++)
{
if(vis[ask[pos][i].first])
ans[ask[pos][i].second]=fnd(gp[ask[pos][i].first]);
}
cnt=G[pos].size();
for(int i=0;i<cnt;i++)
{
tarjan(G[pos][i]);
gp[G[pos][i]]=pos;
}
}
void solve()
{
int n,m,q,a,b;
scanf("%d%d%d",&n,&m,&q);
for(int i=1;i<=n;i++)
{
gp[i]=i;
vis[i]=false;
}
for(int i=1;i<=m;i++)
{
scanf("%d%d",&a,&b);
G[a].push_back(b);
}
for(int i=1;i<=q;i++)
{
scanf("%d%d",&a,&b);
if(a==b)
ans[i]=a;
else
{
ask[a].push_back(P(b,i));
ask[b].push_back(P(a,i));
}
}
tarjan(1);
for(int i=1;i<=q;i++)
printf("%d\n",ans[i]);
}
int main()
{
solve();
return 0;
}
应该不可能有题目直接就询问两个节点的LCA吧(上面的模板是直接询问LCA的)
都是由一堆修饰包裹起来的题目,把他剖析之后才知道是使用LCA的方法去求解
例如,最普通的模板题 HDU2586询问的是树上节点间距离
转换到LCA问题,可以发现两个节点u,v之间的距离就是他们与根节点的距离之和减去两倍的LCA(u,v)与根节点距离之和——令dis[u]为节点u到根节点之间的距离,则DIS(u,v) = ( dis[u] - dis[LCA(u,v)] ) + ( dis[v] - dis[LCA(u,v)] ) = dis[u] + dis[v] - 2*dis[LCA(u,v)]
还有 HDU2874 ,给定的是一个森林(包含多个不连通的树)
询问与上述2586相同,只是如果给定的节点不在同一棵树上需要特殊输出
所以需要再加一个并查集查询是否处于同一颗树
再引入另外一个节点(0)作为森林的根节点,让它指向各棵树的根节点,再从0开始tarjan会更好写一些
此外还有很多问题……
标签:查询 names ble ima 遍历 size 二叉查找树 lse i++
原文地址:https://www.cnblogs.com/stelayuri/p/12650344.html