标签:检查 矢量 png 参数 公式 面积 变更 符号表 follow
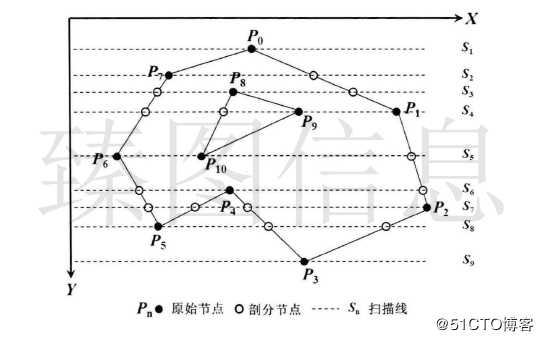
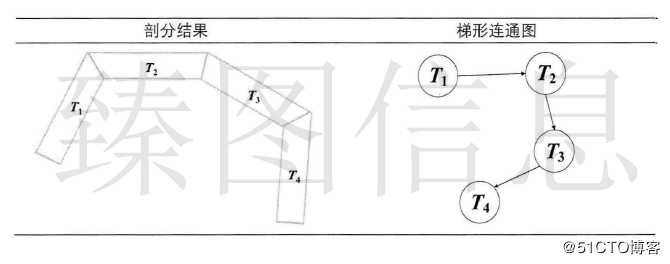
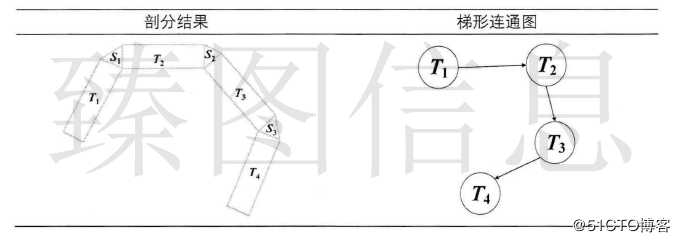
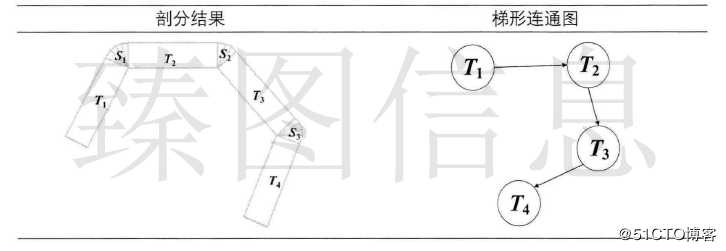
传统矢量地图LOD绘制流程包含简化、剖分与渲染三个步骤。由上述分析可知,传统矢量地图LOD绘制流程中简化与剖分是两个独立的过程,重复的剖分计算导致其渲染效率相对低下。梯形格网方法解决了传统方法中重复剖分的问题,但该方法是在二维场景下的实现且不支持线要素的渲染。本文借鉴梯形格网结构与简化思想,顾及投影方式对地图简化的影响,设计透视投影下梯形格网的简化算法,实现透视投影下矢量地图LOD方法简化与剖分的统一,从而加速地图的渲染。
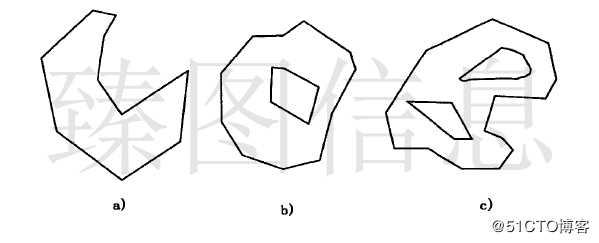
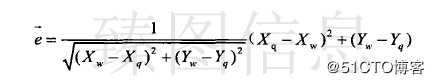

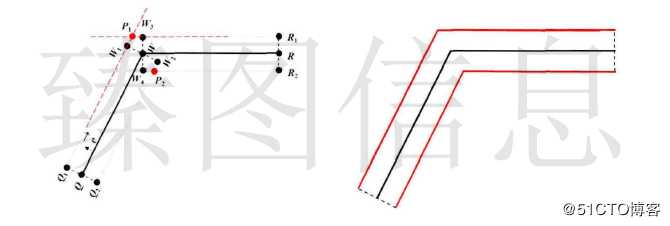
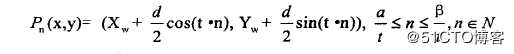
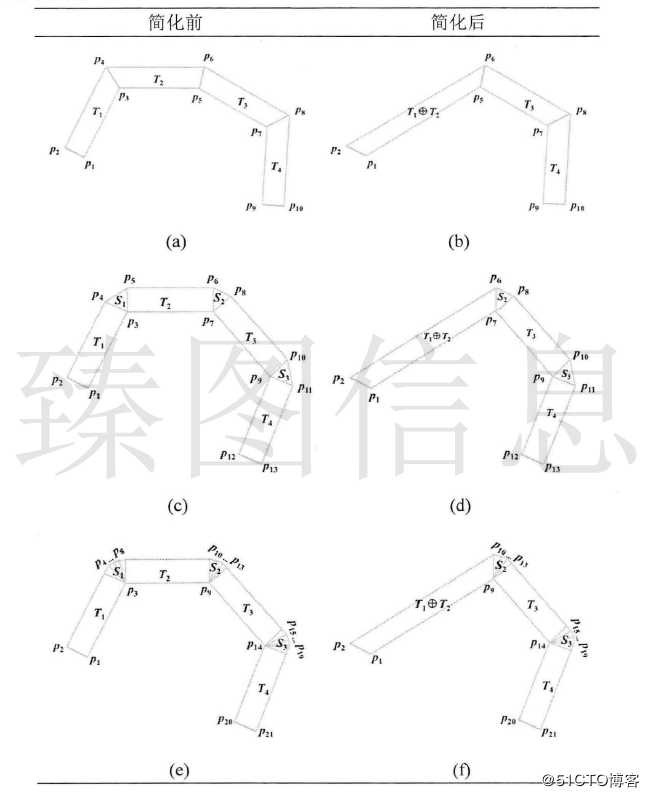
(1)斜角连接样式的梯形格网的合并
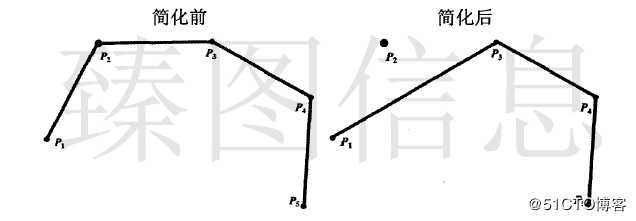
斜角连接连接样式的梯形格网只包含梯形数据,如上图中(a)所示。若T1与T2之间原始数据节点的容差小于当前容差ε,则T1与T2进行合并。合并后结果如上图(b)所示,通过对两个梯形的公共边进行折叠操作实现合并即选取的非公共边的侧边组合成合并后的梯形。
(2)平角连接样式的梯形格网的合并
平角连接的梯形格网包含梯形数据和三角形样式数据,如上图中(c)所示,合并操作需要对梯形数据和样式数据进行合理的组织。若T1与T2之间原始数据节点的容差小于当前容差ε,则T1与T2进行合并。合并后结果如上图(d)所示,T1与T2具有一个公共顶点P3,选择T1中与P3所在侧边对应的侧边和T2中与P3所在侧边对应的侧边组合成新的梯形,并移除S1样式数据完成平角连接梯形格网的合并。
(3)圆角连接样式的梯形格网的合并
圆角连接的梯形格网包含梯形数据和三角扇样式数据,如上图中(e)所示,合并操作需要对梯形数据和样式数据进行合理的组织。若T1与T2之间原始数据节点的容差小于当前容差ε,则T1与T2进行合并。合并后结果如上图(f)所示,合并方式与平角连接相同。
4.2面梯形格网简化算法
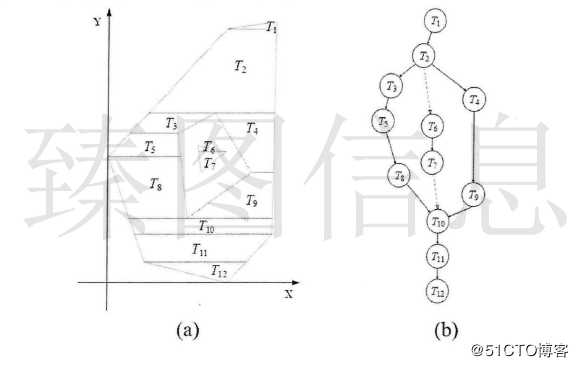
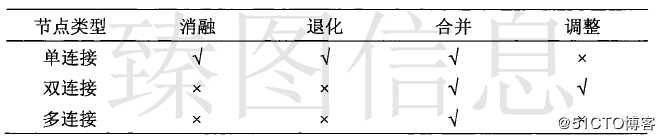
针对面梯形格网结构,本文顾及一致性的原则改进了面梯形格网的简化算法,使其支持透视投影下的简化操作。针对面几何要素的剖分结果,本文设计合并、退化、消融和调整四种简化规则,梯形格网还原过程即是简化过程的回退,在此不再论述。文中将位于同一个梯形且与节点处于相同侧边的顶点称为此节点的垂直顶点,与节点处于相同底边的顶点称为此节点的水平顶点。
(1)合并
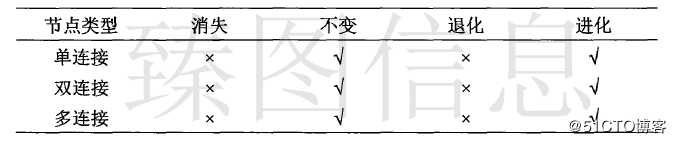
具备相同顶点的两梯形可能发生合并操作,合并后两个梯形变为一个梯形。剖分后直接相连的两个梯形具有一个公共顶点或两个公共顶点。根据公共顶点数量,将具有一个公共顶点的梯形之间合并称为单点合并;具有两个公共顶点的梯形之间合并称为双点合并。
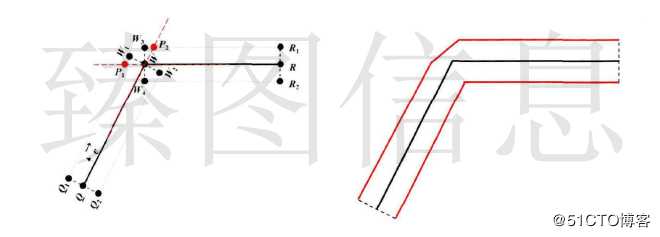
单点合并多发生于梯形连通图的顶端或尾端。一般包含两个具有三个节点的特殊的梯形(三角形)合并或三角形与梯形的合并。如下图(a)所示,若当P3的容差小于当前容差ε则发生合并操作,合并后结果如下图(b)所示,取P3左梯形的左侧边节点与右梯形的右侧边节点为合并后的梯形节点,组合成合并梯形。如下图(c)所示,若当P4的容差小于当前容差ε则发生合并操作,合并后结果如下图(d)所示,取P4左梯形的左侧边节点与右梯形的右侧边节点为合并后的梯形节点,组合成合并梯形。与单点合并操作对应的梯形及节点的变化如下表所示。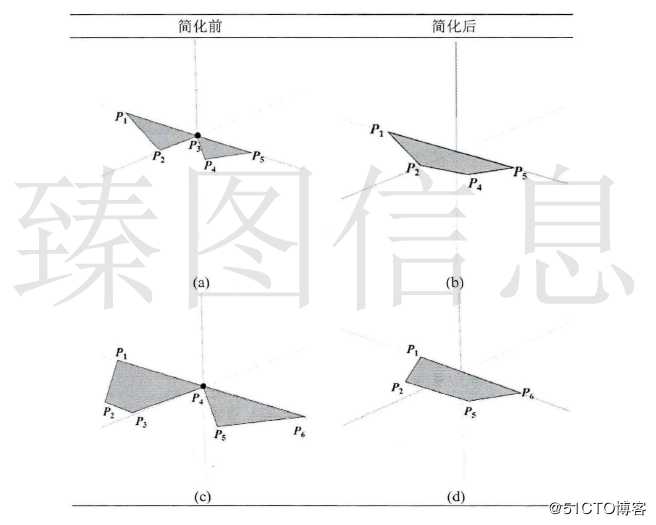

双点合并情况多发生于梯形连通图的链上。双点合并通过两个梯形公共边的折叠操作实现即选取的非公共边的对应边组合成合并后的梯形。如下图(a)所示,Pa为剖分时产生的节点不具备权重值,当P2的容差小于当前容差ε则图形发生双节点合并,合并后的结果如下图(b)所示;如下图(c)所示,当P2、P5的容差皆小于当前容差ε则图形发生双点合并,合并后的结果如下图(d)所示;如下图(e)所示,此时图形非原始剖分图形而为图形简化后的某一状态,当P2、P5的容差皆小于当前容差ε则图形发生双点合并,合并后结果如下图(f)所示。与双点合并对应的梯形及节点的变化如下表所示。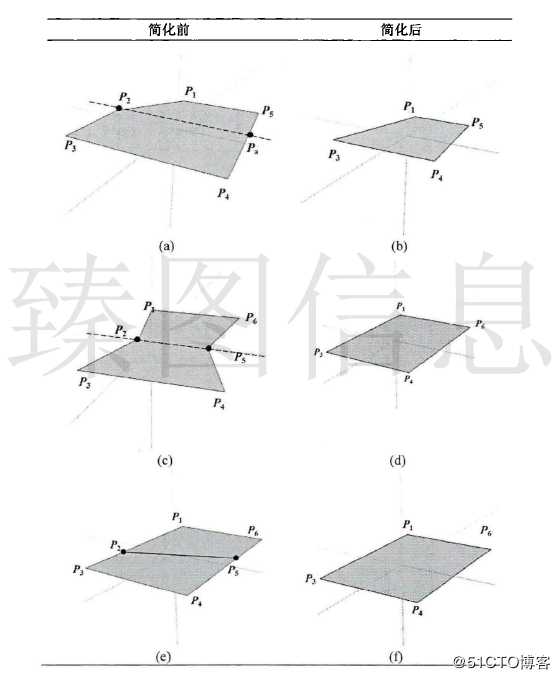


(2)调整
梯形与另一梯形共点且此节点被简化,可能会发生梯形的调整。调整不产生新的梯形,只对梯形的节点进行变更。梯形既有梯形自身的调整又有两个梯形的调整。文中依据调整操作中参与梯形的数目分为单梯形调整和双梯形调整。
单梯形调整一般发生在梯形格网的顶端或尾端。如下图(a)所示,若P7的容差小于当前容差ε,由于P7的垂直顶点为P8则应将P7调整至其上一个节点即P6。如下图(c)所示,若P1的容差小于当前容差ε,由于P1为首节点且其垂直顶点为P2则应将P1调整至其上一个节点即尾节点P11。同理,假设Pn的容差小于当前容差ε,若与Pn对应的梯形垂直节点若为Pn+1,则其应该调整为Pn-1;与Pn对应的梯形垂直节点若为Pn-1,则其应该调整为Pn+1,需考虑Pn为首尾节点的情况。与单梯形调整操作对应的梯形及节点的变化如下表所示。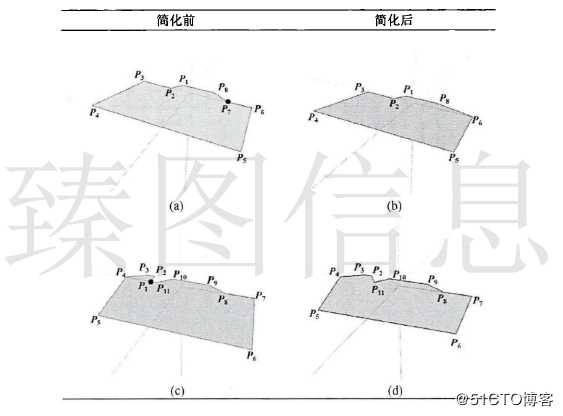

双梯形的调整依据参与调整的梯形之间共点的数目分为单节点连接梯形的调整和双节点连接梯形的调整,以下分别进行介绍。
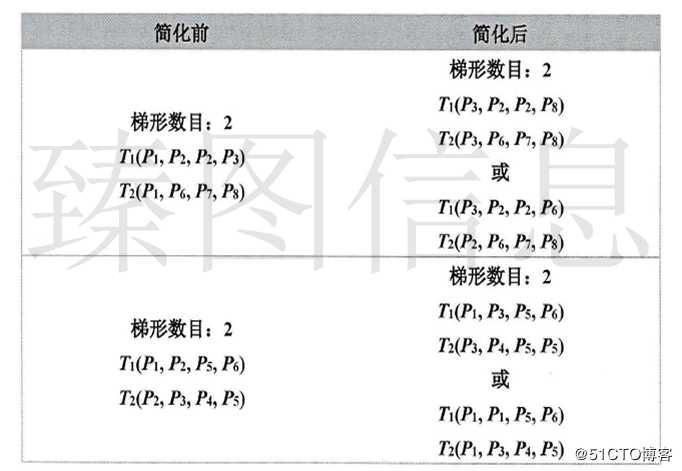
单节点连接的双梯形调整是指参与调整的两个梯形具有一个公共节点,一般发生在梯形格网顶端或者尾端。如下图(a)所示,若P1的容差小于当前容差ε,则包含P1的两个梯形都要进行节点调整,T1中若P1调整为T2中P1的垂直顶点P8或水平顶点P6,则T2中P1调整为P1的水平顶点P3或垂直顶点P2,即得到T1(P3,P2,P2,P8)、 T2(P3,P6,P7,P8)或T1(P3,P2,P2,P6)、T2(P2,P6,P7,P8)两种结果,两种结果在几何图形具有一致性。
双节点连接的双梯形调整是指参与调整的两个梯形具有两个公共节点,一般发生在梯形链上,调整过程中只有一个公共节点被简化。如下图 (c),若P2的容差小于当前容差ε而P5的容差大于当前容差ε,则包含P2的两个梯形都要调整节点。如T1中P2节点被移除或被调整为T2中P2的垂直顶点P3;则T2中P2节点被调整为T1中P2的垂直顶点P1或被移除,可得到T1(P1,P1,P5,P6)、T2(P1,P3,P4,P5)或T1(P1,P3,P5,P6)、T2(P3,P3,P4,P5)两种结果,两种结果在几何图形具有一致性。与双梯形调整操作对应的梯形及节点的变化如下表所示。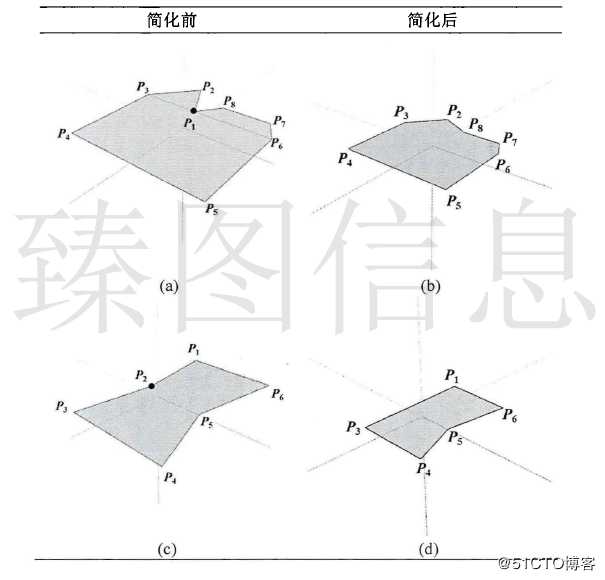
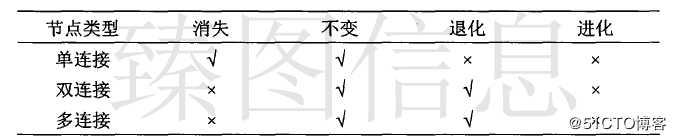
(3)退化与消融
退化是由梯形变为三角形的操作,消融是指有三角形退化为线或消失的操作。退化与消融只发生梯形连通图中链的顶端或尾端的单连接节点上。
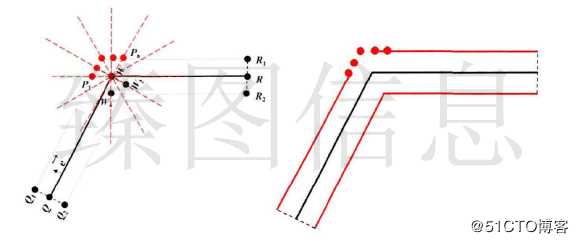
当需要被简化的节点只存在于一个梯形且其水平节点不需被简化,则发生图形退化。如下图(a)中所示若P1的容差小于当前容差ε而P6的容差不小于当前容差ε,则发生图形的退化操作,此节点从梯形节点数组中移除;由于本文研究透视投影下简化方法,节点容差与视点相关,若图形旋转则可能出现P6的容差小于当前容差ε而P1的容差不小于当前容差ε的情况,如下图(c)所示。退化操作对应的梯形及节点的变化如下表所示。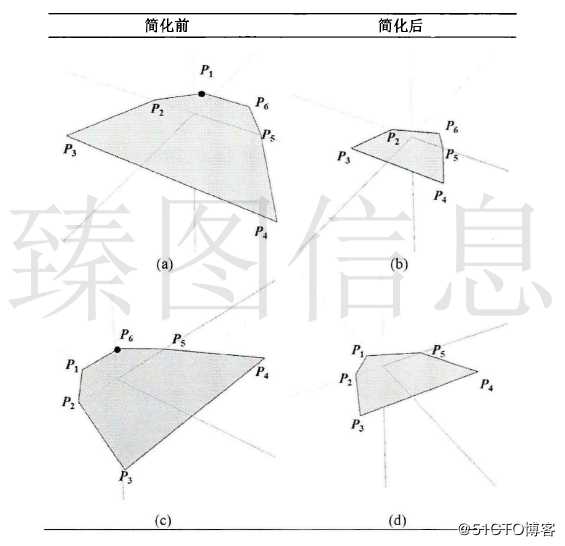

当三角形顶点被简化或梯形两顶部节点都被简化时则发生图形消融。如上图(a)中所示,若P1、P6的容差小于当前容差ε则发生消融。下图(a)中,若P1的容差小于当前容差ε则发生消融,梯形退化为线或变为不可见状态,对应的梯形及节点的变化如下表所示。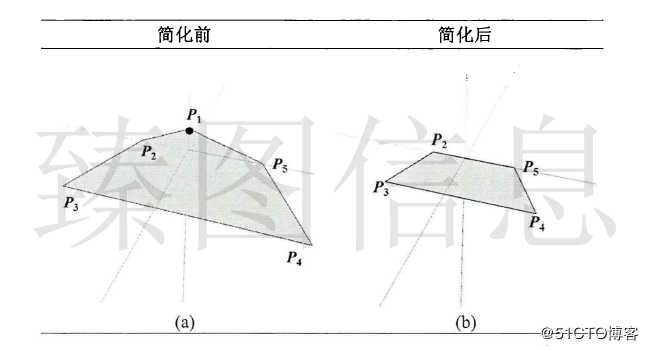

5自相交处理
一执行LOD绘制时应保持拓扑关系的一致性,一般会考虑三种形式的拓扑关系:(1)对于单个边界,边界不应自相交;(2)对于两个边界,外部或内部边界不应自相交;(3)岛屿应该没有交叉点。依据简化算法,简化操作存在引入交叉点的风险,在梯形格网简化算法中,拓扑错误都体现为梯形之间出现交叉点。因此,拓扑检查操作可以转化为检查简化后的梯形是否与其他梯形相交的问题。通过穷举法检查梯形是否与任何其它梯形相交可以避免拓扑误差,然而该方法在计算上可能非常昂贵,尤其是当要检查的多边形包括大量的顶点时,本文使用一种启发式测试策略来有效地检查交叉点。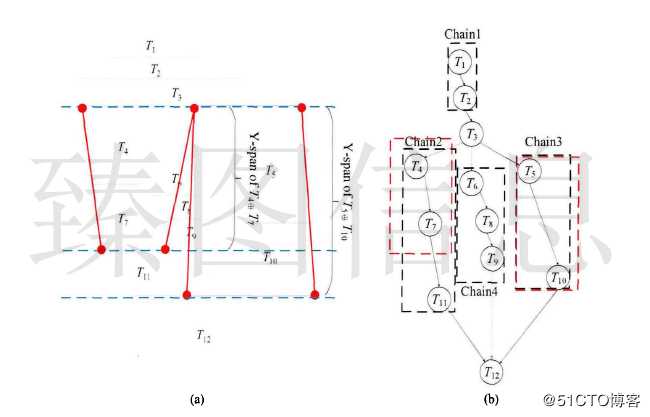
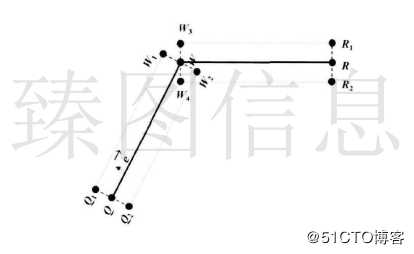
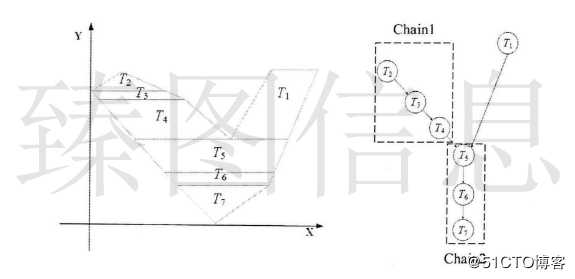
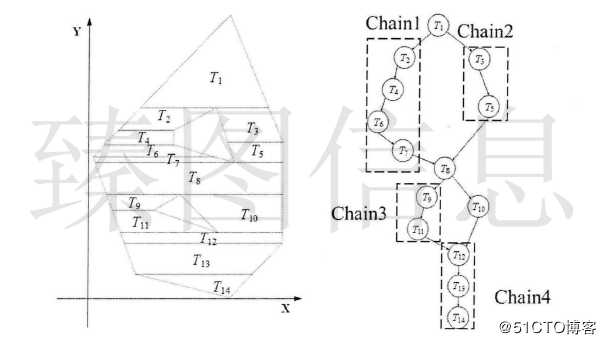
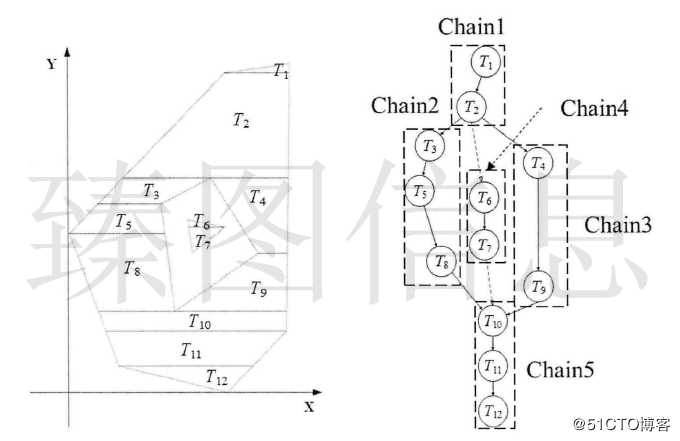
如上图所示,若T4与T7进行简化操作,则不需判断所有梯形与合并的梯形是否相交,可能与合并后梯形相交的区域位于T4与T7最小Y值与最大Y值之间,若合并后的梯形与相邻链Chain4(T6、T8、T9)不相交,则不可能与Chain3(T5、T10)发 生相交。如上图所示,若T5与T10进行简化操作,可能与合并后梯形相交的区域位于T5与T10最小Y值与最大Y值之间。若合并后的梯形与相邻链Chain4(T6、T8、T9)不相交,则不可能与Chain2(T4、T7、T11)发生相交。因此,本文通过对y-span内相邻链的检查实现快速的自相交判断。
6结语
本文构建了线、面要素的梯形格网,并基于一致性和拓扑保持的原则设计透视投影下梯形格网的简化算法。首先介绍了矢量数据结构,从可视化的角度出发采用平行线推移算法和梯形剖分算法对矢量几何要素进行剖分处理。其次,介绍了梯形连通图并详细探讨了梯形节点、梯形链和梯形简化的关系,将矢量几何要素剖分后的结果组织成梯形格网并设计了一种透视投影下梯形格网的简化算法,最终使用一种梯形格网的自相交判断方法避免了可能出现的自相交情况。
原文来自:http://www.ztmapinfo.com/blog/index.php/article/38.html
标签:检查 矢量 png 参数 公式 面积 变更 符号表 follow
原文地址:https://blog.51cto.com/14758767/2485391