贝叶斯分类算法 实现

标签：com   第一个   table   sum   pandas   list   str   image   tab   

（一）贝叶斯理论

1.设x={a1,a2,a3,...,an}为一个待分类项，而a为x的一个特征属性

2.有类别集合C={y1,y2,...,yn}

3.计算P(y1|x), P(y2|x), P(y3|x),...,P(yn|x)

4.比较得出结果

（二）根据训练集计算P(yi|x):

1.统计在各类别下各个特征属性的条件概率

       P(a1|y1), P(a2|y1), .... , P(am|y1)

       P(a2|y1), P(a2|y2), .... , P(am|y2)

       P(am|yn), P(am|yn), ... , P(am|yn)

2.假设各个特征属性之间是相互独立的，根据贝叶斯定理有：

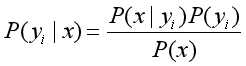
因为分母对于所有类别是常数，所以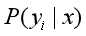正比于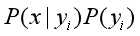

而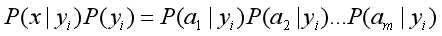

在连续的情况下，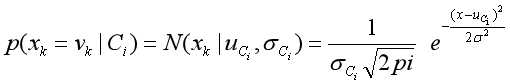

3.以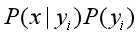最大项作为x的所属类别

   【注】与都代表的是第i种类别，表示第i种类别的平均值，代表第i种类别的标准差

计算（数据来源：iris_15.txt）

数据共有15个samples，因为没有给测试集，所以假定第一个样本

为测试集，其余14个样本为训练集。计算，，

Step1:记Iris-setosa为类别1，Iris-versicolor为类别2，Iris-virginica为类别3；记第一个属性为a1, 第二个属性为a2, 第3个属性为a3, 第4个属性为a4

Step2:计算。

计算1：

对属性a1:

   属性值a1=[5.4, 4.6, 4.9, 5.1, 6.5, 5.7, 6.3, 4.9, 6.6, 6.8, 5.7, 5.8, 6.4, 6.5]

   对于该属性而言,有，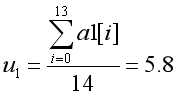

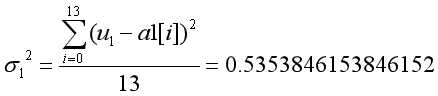
同理算出属性a2,a3,a4

计算2：

对于类别1，有samples

1   5.4  3.9  1.7  0.4      Iris-setosa

2   4.6  3.4  1.4  0.3      Iris-setosa

3   4.9  3.1  1.5  0.1      Iris-setosa

4   5.1  3.3  1.7  0.5      Iris-setosa

对属性a1:,,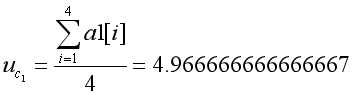

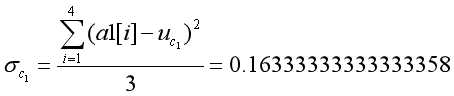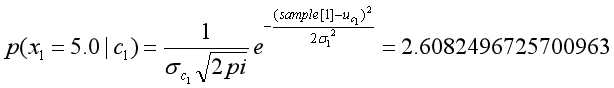
同理算出a2,a3,a4的在类别1下的概率

对于类别二，有测试samples

5   6.5  2.8  4.6  1.5  Iris-versicolor

6   5.7  2.8  4.5  1.3  Iris-versicolor

7   6.3  3.3  4.7  1.6  Iris-versicolor

8   4.9  2.4  3.3  1.0  Iris-versicolor

9   6.6  2.9  4.6  1.3  Iris-versicolor

类别三，有测试samples

10  6.8  3.0  5.5  2.1   Iris-virginica

11  5.7  2.5  5.0  2.0   Iris-virginica

12  5.8  2.8  5.1  2.4   Iris-virginica

13  6.4  3.2  5.3  2.3   Iris-virginica

14  6.5  3.0  5.5  1.8   Iris-virginica

同理分别算出属性在类别2,3的条件概率

（三）得出结果

根据（二）得出的结果算出样本属于类别1，2，3的概率，较大者为样本所属的类别。

实验代码：

import math as Math
import pandas as pd
def fun_average(a):
    sum =0
    for i in range(len(a)):
       sum=sum+a[i]
    return sum/len(a)

def fun_squaresubstract(a,u):
    sum=0;
    for i in range(len(a)):
        sum=sum+(a[i]-u)*(a[i]-u)
    return sum/(len(a)-1)

def fun_p(x,u,temp,all):
    a = 1 / (temp * Math.sqrt(2 * 3.1415926))
    b=-(u-x)*(u-x)/(2*all*all)
    return a*Math.exp(b)

def main():
    data = pd.read_csv(r‘C:\Users\25826\Desktop\datamining\iris.csv‘,header = None)
    data_2=data.tail(14)
    sample=[5.0,3.6,1.4,0.2]
    print(data_2)
    for i in range(4):
        print("第"+str(i)+"个属性")
        data_1=list(data_2[i])
        print(list(data_1))
        average = fun_average(data_1)
        print(average)
        all=fun_squaresubstract(data_1,average)
        print(all)
        a=[]
        a.append(data_1[0:3])
        a.append(data_1[4:8])
        a.append(data_1[9:13])
        for j in range(3):
            ave = fun_average(a[j])
            square = fun_squaresubstract(a[j],ave)
            res = fun_p(sample[i],ave,Math.sqrt(square),all)
            print(ave,square,res)
main()

贝叶斯分类算法 实现

标签：com   第一个   table   sum   pandas   list   str   image   tab   

原文地址：https://www.cnblogs.com/yaggy/p/12667793.html