标签:问题 根据 位置 其他 比较 lse 场景 如何 set
动态规划在计算机中是一个比较玄学的算法,有的人可能看很久都很疑惑这到底是怎么回事,但是一旦理解了,上手就非常容易了。
(以下内容来自百度百科)动态规划(dynamic programming)是运筹学的一个分支,是求解决策过程(decision process)最优化的数学方法。20世纪50年代初美国数学家R.E.Bellman等人在研究多阶段决策过程(multistep decision process)的优化问题时,提出了著名的最优化原理(principle of optimality),把多阶段过程转化为一系列单阶段问题,利用各阶段之间的关系,逐个求解,创立了解决这类过程优化问题的新方法——动态规划。1957年出版了他的名著《Dynamic Programming》,这是该领域的第一本著作。
简单说来,当你希望从现在的状态,通过做出一系列同类型子决策达到最终的目的,而且你的一次决策行为产生的影响又会影响其他的决策条件的时候,就应该考虑动态规划了(一边规划一边动=v=)。可以发现,动态规划问题面临的最大难题就是,虽然你做的每次子决策都是相同类型的,但是每次子决策完成,当前的状态就发生了改变,其他的决策又受到了影响,或者说,子决策会受到某个条件的限制,但决策的发生又对这条件产生影响。
动态规划问题的基本问法是:当状态量为xx时,想要某物理量达到最优,应该如何决策?
动态规划的本质是数学归纳法。也就是说,当状态量的数值为n时,我们可以思考n个问题,即当状态量取值分别问0-n时,达到最优时的决策方案是什么?此时,每一个问题就可以被称为一个状态。由于状态之间的变化是由子决策产生的,即状态 + 子决策 = 新状态,新状态上的最优物理量与前置状态上的最优物理量之间具有某种运算关系,而初始状态是已知的,只要找到某状态下的所有前置状态,归纳两者之间的关系,就可以得到状态转换方程,归纳可以得到最终的状态,从而得出动态规划算法。
涉及多个子决策过程,且这些子决策都是同类型的,即都被某种条件限制,且对某条件产生影响
问题目标是对某个物理量进行选优
有明确的初始状态
问法:已知可以进行某种决策,在状态量为xx的前提下,想要达到最优物理量,应该如何决策?
由此,动态规划的算法应用公式便好理解了:
动态规划算法 = 初始状态(没有进行决策时的条件) + 状态转移方程(新决策做与不做取优)
状态量:范围有限的、约束子决策且被子决策影响的条件,子决策影响的物理量 - 选优的物理量
流程:
1. 确定子决策:找到子决策的n种方向
2. 确定状态量:找到每次决策后到达的新状态
3. 确定最优物理量:最优目标
4. 确定初始状态:在不进行任何决策行为时,各个状态上最优物理量的值
5. 状态转移方程:找到前置状态与新状态之间的关系,编写状态转移方程
以背包问题为例:如果按照贪心策略,我们自然考虑将单位体积价值更高的物品装入背包,从而使得背包对应的体积得到价值最大化,但是这样做的问题是,我们需要达成的结果是背包最后的单位体积价值最大,如果放入某一单位体积价值更高的物品之后,剩余的体积无法放入其他物品,那背包的平均单位体积价值可能反而更小,比如,有1个体积为15的包,1个体积为11价值为10的物品和3个体积为5价值为4的物品,很明显放入3个体积为5的物品总价值最高。
此时,问题可以转化为:“已知可以选择是否将某物体放入背包,在背包的容量为15的情况下,想要背包价值最高,应该如何决策?”。显然,子决策集合就是对于每一个物品,决策是否将其放入背包,状态就是当前的背包容量。
这样的问题可以通过暴力破解,即对决策情况进行排列组合,统计满足容积限制时的最大价值,这样的解题思路类似于画决策树,每一层都是一个子决策的确定
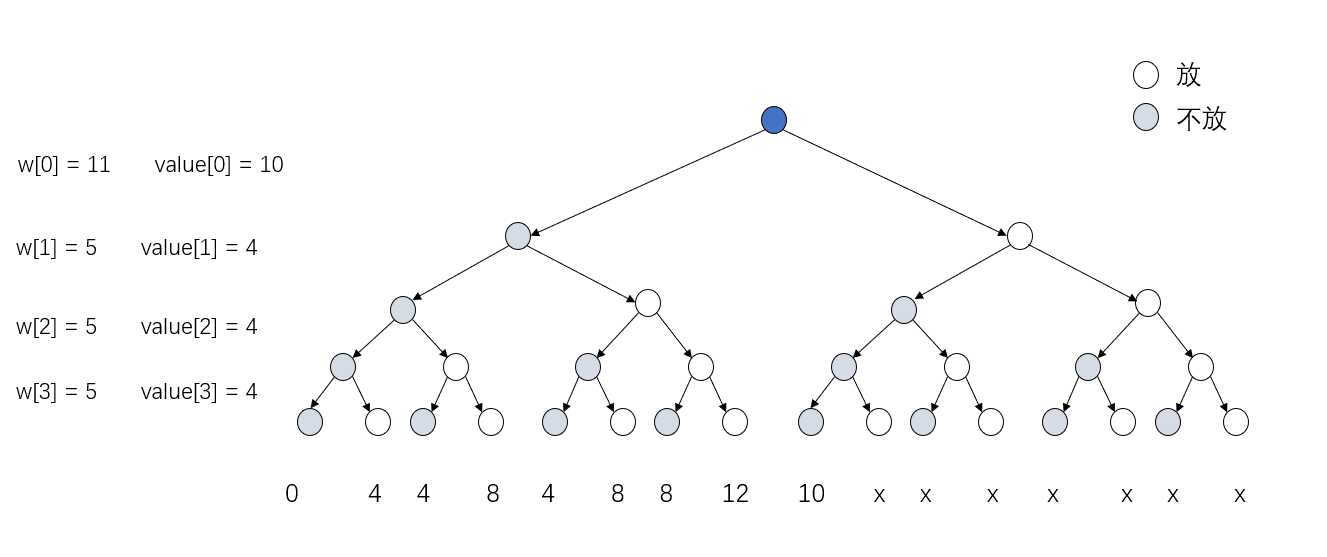
我们发现,如果将目标限制条件为15,逐一完成子决策,并在最后统计最大价值,本质是枚举法,这是十分浪费时间的,且当问题规模过大时,是无法解决问题的。
我们考虑以下定理
定理1:假如物体i在容积为V的背包的最大价值组合S中,此时最大价值为f,那么如果在容积为V-w[i]的背包中放置除i号外的其他物体,最佳组合一定是S/i(S中去除i号物体),最大价值一定是f-va[i]
证明:如果有更优的组合使得价值f1>f-va[i],那么容积为V的背包的最大价值应该为f1+va[i] > f-va[i]+va[i] = f,矛盾
定理2:假如0 - n-1号物体分别放入体积为0-V的包中的最佳组合都已知,最大价值分别使用f[n-1][0]、...、f[n-1][V]表示,那么,如果添加n号物体 f[n][V] = max{f[n-1][V], f[n-1][V-w[n]]+va[n]}
证明:由于已知前n-1个物体的放置情况,对于新增的第n个物体,(1)如果它不会出现在最佳组合中,那么最佳组合仍旧是前n-1个物体的组合情况,也就是f[n-1][V];(2)如果它会出现在最佳组合中,结合定理1,在容积为V-w[n]的背包中,如果放入0到n-1号物体,最大价值一定是f[n][V]-va[n],而已知这个最大价值为f[n-1][V-w[n]],所以 f[n][V] = f[n-1][V-w[n]] + va[n];由于两种情况不确定,所以我们只需要选择最大的结果作为最大价值结果。
首先,我们将物体标号序号,已知将前0个物体分别放入体积为0-V的背包中时,最大价值都为0,根据数学归纳法,我们可以逐步求出来前1个,前2个...前n个物体分别放入0-V的背包中的最大价值,最后得到的f[n][V]就是我们的最终目标。
问题场景已经很清晰了,我们这里套用公式来完成动态规划算法的分析的实现。
首先,我们需要分析出什么是子决策,子决策是针对一系列对象进行的相同类型的决定,在背包问题中,子决策应该是每一次操作都是决定是否将某一个物品放入背包。
其次,我们需要确定该问题状态量到底是什么,前文提到,状态量就是子决策影响的物理量S - 选优的物理量F。在背包问题中,每次放或不放一个物体时,背包的已用空间和背包的价值都会变大,其中,背包的价格是选优的物理量,所以状态量是当前的容积,容积为整数,所以共有V+1个状态
然后,我们需要判断什么是最优物理量,在背包问题中,选优的方向是使得背包具有的价值最大
接着,根据已知的内容判断初始状态:当永远不进行决策时,最优物理量永远为0
最后,我们考虑写出状态转移方程,写出状态转移方程的主要方法是,每对于每一种决策,找到当前状态与前置状态的关系,根据前置状态计算当前状态的最优物理量,并在这些决策中选最优:f[n][V] = max{f[n-1][V], f[n-1][V-w[n]]+va[n]}
编写代码时,只需要两个循环即可完成
for(int i = 1; i < n+1; ++i){ // 依次确定不同决策后不同状态的选优值
for(int j = 0; j < V+1; ++j){ // 对第i次决策过程,确定不同状态的选优值
f[i][j] = max{f[i-1][j], f[i-1][j-w[i]]+va[i]};
}
}
return f[n][V];
#include <iostream>
#include <algorithm>
using namespace std;
int main(){
int weight[4] = {11, 5, 5, 5};
int value[4] = {10, 4, 4, 4};
int max_value[5][16];
for(int i = 0; i < 5; i++){
for(int j = 0; j < 16; ++j){
max_value[i][j] = 0;
}
}
for(int i = 1; i < 5; ++i){
for(int j = 1; j < 16; ++j){
if(j-weight[i-1] >= 0){
cout << "check " << i << " " << j << endl;
max_value[i][j] = max(max_value[i-1][j], max_value[i-1][j-weight[i-1]]+value[i-1]);
cout << "set " << i << " " << j << " " << max_value[i][j] << endl;
}
else{
max_value[i][j] = max_value[i-1][j];
}
}
}
cout << max_value[4][15] << endl;
}
有一条由21片何叶依次相连组成的路,青蛙初始时站在第一片荷叶上,每次可以选择跳到下一片荷叶上,或者越过下一片荷叶跳到第二片上,请问最后到达最后一片荷叶上时,有几种跳法?
青蛙每跳一次,后面的荷叶数量就相应变少,荷叶数量又限制了青蛙可以跳的距离,所以可以考虑使用动态规划
确定子决策:跳一步或者跳两步,共两种决策
状态量:青蛙所在位置,从第一片荷叶开始到最后一片,共21个状态
确定最优物理量:跳法数量最大jump_num
确定初始状态:永远不决策时,初始为1
状态转移方程:当决策为跳n步跳到第s片荷叶上时,前置状态为第s-n片荷叶,若前置状态为t种跳法,那么当前状态也为t种跳法;n有两种赋值即1,2,结合物理意义,s状态的跳法 = s-1状态跳法 + s-2状态跳法
jump_num[s] = jump_num[s-1] + jump_num[s-2]
#include <iostream>
#include <algorithm>
using namespace std;
int main(){
int jump_num[21] = {0};
jump_num[0] = 1;
for(int i = 1; i < 21; ++i){
int add = jump_num[i-1];
jump_num[i] = i > 1 ? jump_num[i-1] + jump_num[i-2] : jump_num[i-1];
}
for (int i = 0; i < 21; ++i){
cout << jump_num[i] <<" ";
}
cout << endl;
return 0;
}
算法应用公式(二)动态规划 Dynamic Programming
标签:问题 根据 位置 其他 比较 lse 场景 如何 set
原文地址:https://www.cnblogs.com/suata/p/12676904.html