标签:频繁 比较 span 规则 计算 时间复杂度 线段树 get src
一、使用场景
频繁修改场景下用于求前缀和 前缀积等(区间和可以通过前缀和计算而来)
查询和修改的时间复杂度都是O(logN)
二、原理
如求前缀和
(树桩数组只是存一段区域的统计值,业务自己决定,如果求前缀和就存这段区域的和;如果求出现次数就存这段区域的数出现的次数)
一个原始数组A 对应一个树桩数组C
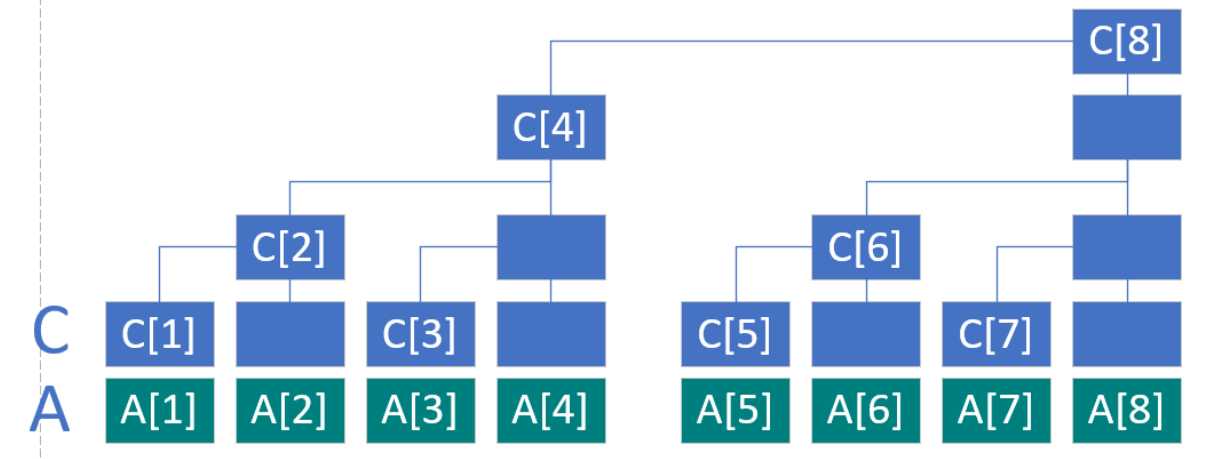
C[1]=A[1] (区间范围 :包含前1个数,包含本身)
C[2]=A1+A2 (区间范围 :包含前2个数)
C[3]=A3 (区间范围 :包含前1个数)
C[4]=A1+A2+A3+A4 (区间范围 :包含前4个数)
C[n] 肯定是包含A[n]的(假设数组从1开始)
线段树采用二分的思想,每个节点表示的范围不断对半分
而数组数组每个元素表示的区间范围(从当前位置往前算)是由 此数的二进制数计算而来
规则如下:第x个数表示的区间范围=2^k (k=二进制(x)末尾0的个数)
如第1个数: 二进制为 00000001 ,末尾0的个数为0,则区间范围=2^0=1
第2个数:二进制为00000010, 末尾0的个数为1,则区间范围=2^1=2
第3个数:二进制为00000011,末尾0的个数为1,则区间范围=2^0=1
第4个数:二进制为00000100,末尾0的个数为2,则区间范围=2^2=4
可以发现:
如果奇数的话 区间范围=1
而任何一个数天然都可以采用二进制表示如6=00000110=2^2+2^1=4+2 ;
则前6个数的区间值可以分解为前4个数的区间值 + 前2个数的区间值
这个规则牛人已经为我们可以
树桩数组第n个数C[n]表示的区间范围=2^k (k=二进制(n)末尾0的个数) = n& (-n)
可以定义函数lowbit(n) 表示区间范围
private int lowbit(int n) {
return n & -n;
}
三、单点更新
修改某个节点 则对应的树桩数组受影响的C[n]都需要改变
如A[6]增加了1 ,则C[6]肯定也需要+1
下一个受影响区间只要包含第6个数,则一样需要更新,下一个受影响的是C[8],下下一个C[16]
规则:A[n]变换 需要变化的树桩数组节点如下
C[n] C[n + logbit(n)] .. C[m] C[m+logbit(m)] .....
代码如下
void updata(int i,int k){ //在i位置加上k
while(i <= n){
c[i] += k;
i += lowbit(i);
}
}
四、前缀和 积
求前n个数的和
preSum(n) = C[n] + C[n-lowbit(n)] + ...+C[m] + C[m-lowbit(m)] + ....+ C[1]
如preSum(6) = C[6] + C[4]
C[6] : 区间范围5-6的值
C[4]:区间范围1-4的值
加起来正好=前6个数的区间值
代码如下
int getsum(int i){ //求A[1 - i]的和
int res = 0;
while(i > 0){
res += c[i];
i -= lowbit(i);
}
return res;
}
五、矩阵和
二维树桩数组(三维 多维)
如下求区域的和 = preSum(5,6) - preSum(2,6) - preSum(5,3) + preSum(2,3)
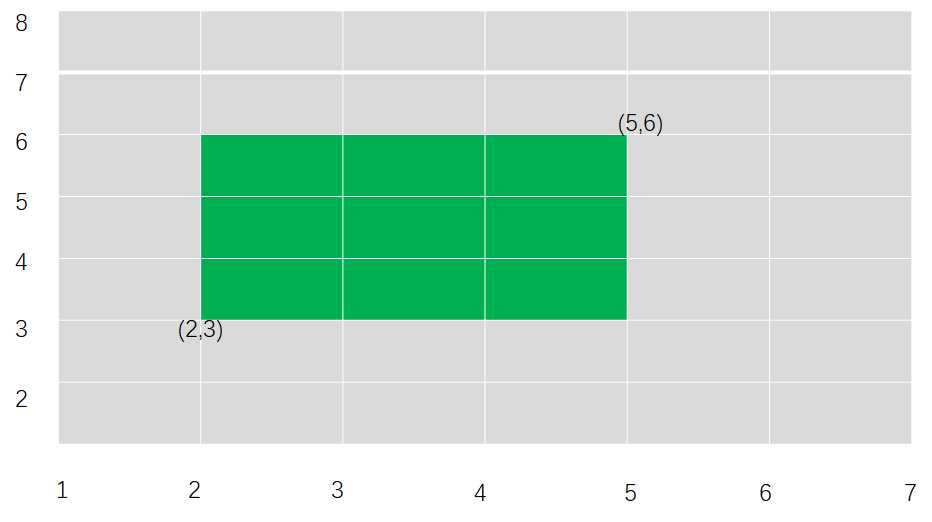
相关代码 2层循环
// 查询
int sum(int i, int j){
int res = 0;
for(int x = i; x; x -= lowBit(x))
for(int y = j; y; y -= lowBit(y))
res += C[x][y];
return res;
}
// 修改
void change(int i, int j, int delta){
for(int x = i; x < MAX_N; x += lowBit(x)) {
for (int y = j; y < MAX_N; y += lowBit(y)) {
C[x][y] += delta;
}
}
}
六、应用(树桩数组求逆序对)
求 1 3 8 5 2 数组有多少个逆序对
直接拿值最为数组下标定义A[8] 对应的树桩数组C[8]
循环遍历每个数m 对应的A[n]就add 1, 树桩数组也对应更新
则前n个数对应与当前数m相比的逆序对=总的数n - preSum(m)
伪代码
for(int i=1;i<=n;i++) {
add(m);
ans+=i-sum(m);
}
此时如果数组非常大 ,则需要先做离散化
如原数组为 1 1000 20000 4 9 有点数值比较大 直接以最大值作为数组下标不合适
可以把数据离散到固定的区间内 保持相对大小不变即可
一种可行的方法:
1、对原数组排序 并记录原来每个数组对应index
2、把排序好的数 直接用 1 2 3 .. 顺序替代,再按原index的位置顺序放入
原数组为 1 1000 20000 4 9-->则离散化之后的数组为 1 4 5 2 3
标签:频繁 比较 span 规则 计算 时间复杂度 线段树 get src
原文地址:https://www.cnblogs.com/yangfei629/p/12676958.html