标签:查找 mat 速度 最大 第一个 数组 col 简单 ***
1 原理
插入排序(Insertion-Sort)的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入
插入排序的工作方式非常像人们排序一手扑克牌一样。开始时,我们的左手为空并且桌子上的牌面朝下。然后,我们每次从桌子上拿走一张牌并将它插入左手中正确的位置。为了找到一张牌的正确位置,我们从右到左将它与已在手中的每张牌进行比较,如下图所示:

2 思路
3 举例
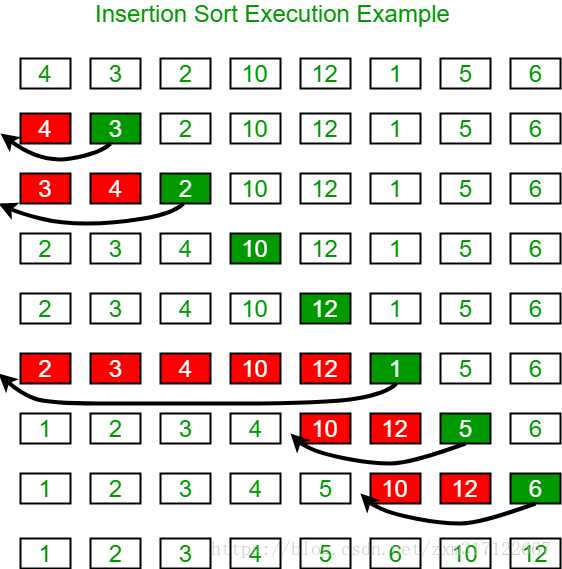
第1趟排序:
把3放到前面这个{ 4 }的数组,依次比较,然后把3放到4前面
第2趟排序:
把2放到前面{ 3 , 4 }的数组,依次比较,然后把2放到最前面
第3趟排序
把10放到前面{ 2, 3 ,4 } 的数组,依次比较,然后放到最后面
第4趟排序
把12放到前面{ 2, 3 , 4 10 }的数组,依次比较,然后放到最后面
第5趟排序
把1放到前面{ 2 , 3 , 4 , 10 , 12}的数组,依次比较,然后放到最前面
.......后面省略
4 时间复杂度

最坏时间复杂度—Θ(n2)
如果数组是倒序的,每次插入就相当于在数组的第一个位置插入数据。比如将 0 插入到数组[2, 3, 5, 7, 11]中,因为数组中的元素都大于 0 ,所以
需要需要与数组中的所有元素进行比较并以此将元素向右移动,最终将0 插入到数组第一个位置。通常来讲,假设数组的length为n,将元素插入到数组的操作称为insert,被插入元素Key需要与数组元素进行比较的此时称为K。 那么在这种情况下,将某一个元素插入到数组时 k = n - 1。
综上所述,在插入排序的流程中,第一次进行insert时K = 1,第二次K = 2, 第三次K = 3…最后一次K = n - 1.因此插入排序所用的总的时间为:
1 + 2 + 3 + ? (n−1) = (1+2+3+?+(n−1)) = n2 / 2 - n / 2 用big-Θ表示法表示就是 Θ(n2)
最好时间复杂度—Θ(n)
那么插入排序可以使用少于Θ(n2) 的时间吗 ? 答案是肯定的。如果要排序的数据已经是有序的,我们并不需要搬移任何数据。从尾到头在有序数据组里查找插入位置每次只需要比较一个数据就能确定插入的位置,所以这种情况下,最好时间复杂度是Θ(n)
平均时间复杂度
试想一下,如果被插入数组的排序是随机的,那感觉概率学,平均情况下此数组中的每一个元素都会比其它一半的元素小。
基于这样的一个概念下,调用insert往数组中插入元素时就需要进行 K/2 次比较。同事插入排序会固定执行 N - 1 此insert操作,所以插入排序的平均时间复杂度也是 Θ(n2)
5 插入排序逐步分析
// 插入排序 逐步分析 public static void insertSort(int[] arr) { // 使用逐步推到的方式来讲解 遍历理解 // ******************第1趟************************ // {101,34,110,1} => {34,101,119,1} // 定义待插入的数 int insertVal = arr[1]; int insertIndex = 1 - 1;// 即arr[1]的前面这个数的下标 // 给insertIndex找到插入的位置 // 说明: // 1 insertIndex >= 0 保证在给insertVal 插入位置 不越界 // 2 insertVal < arr[indexIndex] 待插入的数 还没有找到插入位置 // 3 就需要将arr[insertIndex]后移 while (insertIndex >= 0 && insertVal < arr[insertIndex]) { // {101,34,119,1} -> {101,101,119,1} arr[insertIndex + 1] = arr[insertIndex]; insertIndex--; } // 当退出while循环时,说明插入的位置找到,insertIndex + 1 arr[insertIndex + 1] = insertVal; System.out.println("第一轮插入" + Arrays.toString(arr)); // *******************第2趟**************************** insertVal = arr[2]; insertIndex = 2 - 1; while (insertIndex >= 0 && insertVal < arr[insertIndex]) { // {101,34,119,1} -> {101,101,119,1} arr[insertIndex + 1] = arr[insertIndex]; insertIndex--; } // 当退出while循环时,说明插入的位置找到,insertIndex + 1 arr[insertIndex + 1] = insertVal; System.out.println("第二轮插入" + Arrays.toString(arr)); // *********************第三轮*********************** insertVal = arr[3]; insertIndex = 3 - 1; while (insertIndex >= 0 && insertVal < arr[insertIndex]) { // {101,34,119,1} -> {101,101,119,1} arr[insertIndex + 1] = arr[insertIndex]; insertIndex--; } // 当退出while循环时,说明插入的位置找到,insertIndex + 1 arr[insertIndex + 1] = insertVal; System.out.println("第三轮插入" + Arrays.toString(arr)); }
6 通过for循环实现插入排序(优化版)
// 通过for循环实现插入排序 public static void insertSort3(int[] arr) { int insertVal; int insertIndex; for (int i = 1; i < arr.length; i++) { // 定义每次要插入的值 insertVal = arr[i]; // 因为要将值插入到前面一个数 insertIndex = i - 1; while (insertIndex >= 0 && insertVal < arr[insertIndex]) { arr[insertIndex + 1] = arr[insertIndex]; insertIndex--; } //优化 判断 //如果判断以后发现该数就在它应该存在的位置,那么这个时候就不用交换 //也就是当我想把一个数插入到前面的数组中时,该数正好是最大的,直接放在 //数组的最末尾即可, 也就是inserIndex+1 也就是插入索引 //而i为待插入的索引 if (insertIndex + 1 != i) { arr[insertIndex + 1] = insertVal; } } }
7 插入排序速度测试
public static void main(String[] args) { // *****************插入排序速度测试******************************* // 创建80000个随机的数组 int[] arr = new int[80000]; for (int i = 0; i < arr.length; i++) { arr[i] = (int) (Math.random() * 800000); } // 显示排序前的数组 //System.out.println("排序前" + Arrays.toString(arr)); SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss"); Date date1 = new Date(); String time1 = simpleDateFormat.format(date1); System.out.println("排序前的时间为:" + time1); // 插入排序 调用上面的方法 insertSort2(arr); Date date2 = new Date(); String time2 = simpleDateFormat.format(date2); System.out.println("排序后的时间为:" + time2); }
80000个数据通过普通的插入排序需要时间3秒所有
标签:查找 mat 速度 最大 第一个 数组 col 简单 ***
原文地址:https://www.cnblogs.com/wangxiucai/p/12676998.html