标签:image min svg octave code 想法 mil 正是 输入
------------恢复内容开始------------
垃圾邮件的处理可以作为一个分类问题的例子,要么是垃圾邮件,要么不是垃圾邮件两种可能,这是一种二元的分类问题
0 表示正类,1 表示负类;他们并没有明确的定义,我们可以根据自己的想法来
那么如何来开发分类问题
假如我们用现行回归的方式来做分类的问题(0表示没有恶性肿瘤,1表示有恶性肿瘤)
如图中拟合的红色线所示,我们的预测是正确的,但是如果我们拟合的直线如图中的蓝色所示,我们会有偏差
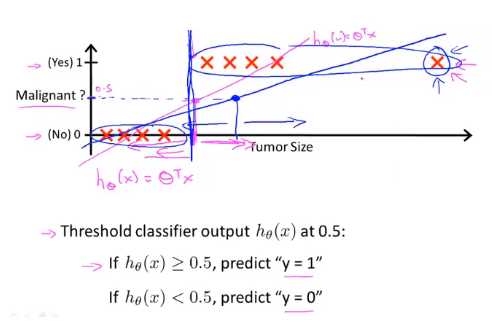
显然我们用回归的方式来解决分类问题是很不明智的
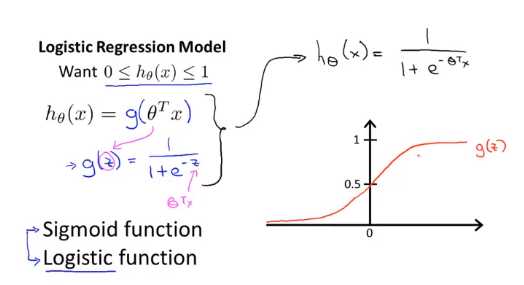
当我们有有个分类问题的时候我们要使用哪个方程来表示我们的假设
此前我们说过,希望我们的分类器的输出值在0和1之间,因此,我们希望想出一个满足某个性质的假设函数,这个性质是它的预测值要在0和1之间。
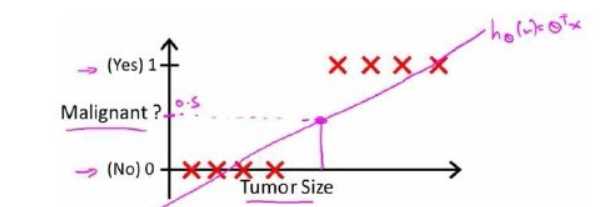
Python代码的实现
import numpy as np
def sigmoid(z):
return 1 / (1 + np.exp(-z))

现在讲决策边界(decision boundary)的概念。这个概念能更好地帮助我们理解逻辑回归的假设函数在计算什么。
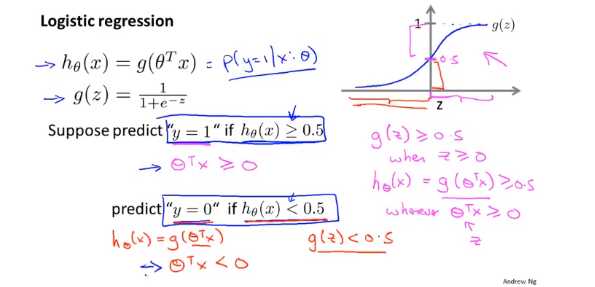
以下是一些栗子


如何拟合逻辑回归模型的参数 θ ,具体来说,我要定义用来拟合参数的优化目标或者叫代价函数,这便是监督学习问题中的逻辑回归模型的拟合问题。

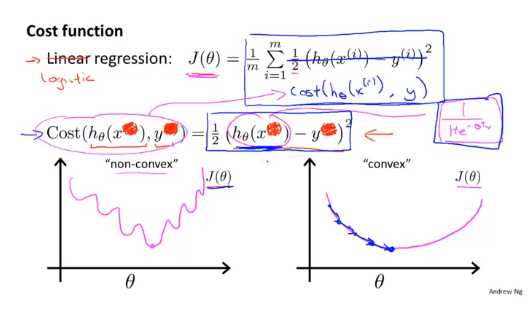


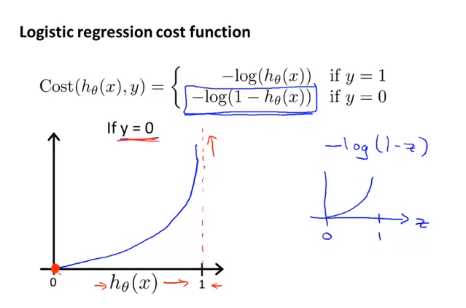
以上的方法构建的函数的的解释为:当实际的 y=1 且 hθ(x) 也为 1 时误差为 0,当实际的 y=1 且 hθ(x) 也不为 1 时,误差随着 hθ(x) 减小而增大,当实际的 y=0 且 hθ(x) 也为 0 时误差为 0,当实际的 y=0且 hθ(x) 也不为 0 时,误差随着 hθ(x) 增大而增大
我们将会找出一种稍微简单一点的方法来写代价函数,来替换我们现在用的方法。同时我们还要弄清楚如何运用梯度下降法,来拟合出逻辑回归的参数。
你就应该知道如何实现一个完整的逻辑回归算法。

如果你把这个更新规则和我们之前用在线性回归上的进行比较的话,你会惊讶地发现,这个式子正是我们用来做线性回归梯度下降的。
那么,线性回归和逻辑回归是同一个算法吗?要回答这个问题,我们要观察逻辑回归看看发生了哪些变化。实际上,假设的定义发生了变化。

我们之前在谈线性回归时讲到的特征缩放,我们看到了特征缩放是如何提高梯度下降的收敛速度的,这个特征缩放的方法,也适用于逻辑回归。如果你的特征范围差距很大的话,那么应用特征缩放的方法,同样也可以让逻辑回归中,梯度下降收敛更快。


下面是我根据以上的教程敲的代码
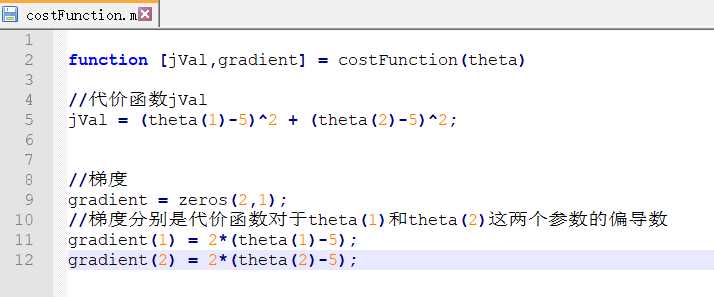
下面是在octave里调用的过程
options=optimset(‘GradObj‘,‘on‘,‘MaxIter‘,100);
initialTheta=zeros(2,1);
[optTheta, functionVal, exitFlag]=fminunc(@costFunction, initialTheta, options);
写一个函数,它能返回代价函数值、梯度值,因此要把这个应用到逻辑回归,或者甚至线性回归中,你也可以把这些优化算法用于线性回归,你需要做的就是输入合适的代码来计算这里的这些东西。
现在你已经知道如何使用这些高级的优化算法,有了这些算法,你就可以使用一个复杂的优化库,它让算法使用起来更模糊一点。因此也许稍微有点难调试,不过由于这些算法的运行速度通常远远超过梯度下降。
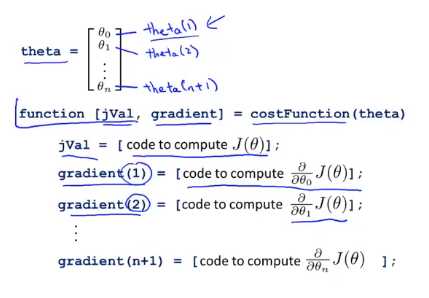
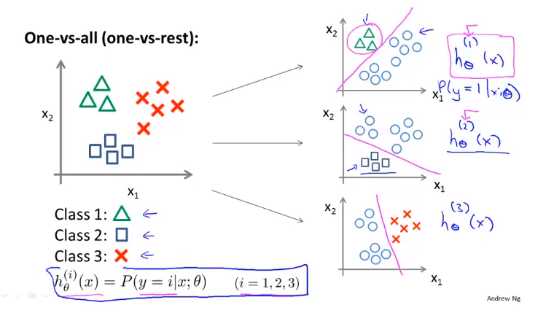
下面是我们针对这样的问题训练的一个逻辑回归分类器
标签:image min svg octave code 想法 mil 正是 输入
原文地址:https://www.cnblogs.com/lmr7/p/12714994.html