基于Matlab用遗传算法求一元函数最值问题（附源码）

标签：数值   遗传算法   参数   操作   pre   进制   问题   要求   val   

问题：求y=10cos(5xx)+7sin(x-5)+10xx的最小值
要求：（1）用遗传算法编程求解问题
（2）编程语言用MATLAB 或C
（3）输出问题的最优解及最大值，并绘图显示

方法一

function.m

clear all;
close all;
clc;
x=-1:0.01:0;
y=10.*cos(5.*x.*x)+7.*sin(x-5.0)+10.*x.*x;
figure
plot(x,y)
grid on
xlabel(‘x‘)
ylabel(‘f(x)‘)
title(‘f(x)=10*cos(5*x*x)+7*sin(x-5)+10*x*x‘)
%%f(x)=10*cos(5*x*x)+7*sin(x-5)+10*x*x

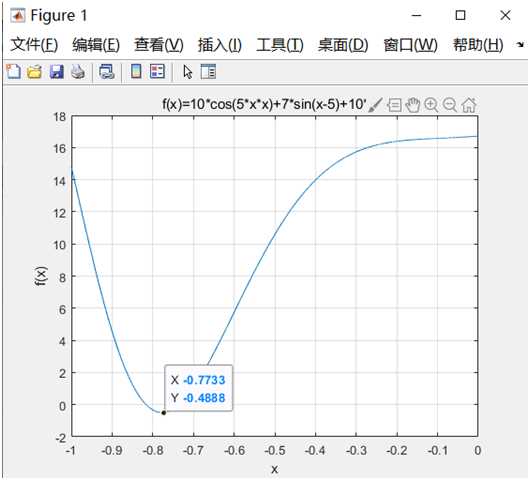
1）运行结果
函数取（-1，0）定义域，能够显示出的X=-0.7733时，Y=-0.4888，图像如下

方法二

func.m

clear all;
close all;
clc;
x=-1:0.01:0;
y=10.*cos(5.*x.*x)+7.*sin(x-5.0)+10.*x.*x;
figure
plot(x,y)
grid on
xlabel(‘x‘)
ylabel(‘f(x)‘)
title(‘f(x)=10*cos(5*x*x)+7*sin(x-5)+10*x*x‘)
%%f(x)=10*cos(5*x*x)+7*sin(x-5)+10*x*x

main.m

clear all;      %清除所有变量
close all;      %清图
clc;            %清屏
nvars = 1;
LB = -1;
UB = 0;
[t,fval] =ga(@test,1,[],[],[],[],LB,UB)

fplot(@(x)(10.*cos(5.*x.*x)+7.*sin(x-5)+10.*x.*x),[-1 0]);
hold on;
plot(t,fval,‘*‘);
function y = test(x)
y = 10*cos(5*x*x)+7*sin(x-5)+10*x*x
end

simple_fitness.m

%目标函数
x = -1:0.01:0;
%y=10*cos(5*x*x)+7*sin(x-5)+10*x*x;
y=10.*cos(5.*x.*x)+7.*sin(x-5)+10.*x.*x;
plot(x,y);
%%%%%%%%%%%%%%%初始化参数%%%%%%%%%%%%%%%
clear all;      %清除所有变量
close all;      %清图
clc;            %清屏
NP=50;          %种群规模（数量）
L = 20;         %二进制位串长度
Pc = 0.8;       %交叉率
Pm = 0.1;       %变异率
G = 100;        %最大遗传代数
Xs = 1;        %上限
Xx = -0;         %下限
f = randi([0,1],NP,L);%随机获得初始种群
xB =[];
%%%%%%%%%%%%%%%遗传算法循环%%%%%%%%%%%%%%%
for k = 1:G
    %%%%%%%%%%%%%%%将二进制解码为定义域范围内十进制%%%%%%%%%%%%%%%
    for i = 1:NP
        U = f(i,:);
        m = 0;
        for j = 1:L
            m = U(j)*2^(j-1)+m;
        end
        x(i) = Xx+m*(Xs-Xx)/(2^L-1);
        Fit(i) = 1/func1(x(i));
    end
    maxFit = max(Fit);
    minFit = min(Fit);
    rr = find(Fit==maxFit);
    fBest = f(rr(1,1),:);
    xBest = x(rr(1,1));
    xB(i)=xBest;
    Fit = (Fit-minFit)/(maxFit-minFit);
    %%%%%%%%%%%%%%%基于轮盘赌的复制操作%%%%%%%%%%%%%%%
    sum_Fit = sum(Fit);
    fitvalue = Fit./sum_Fit;
    fitvalue = cumsum(fitvalue);
    ms = sort(rand(NP,1));
    fiti = 1;
    newi = 1;
    while newi <= NP
        if (ms(newi)) < fitvalue(fiti)
            nf(newi,:) = f(fiti,:);
            newi = newi + 1;
        else
            fiti = fiti+1;
        end
    end
    %%%%%%%%%%%%%%%基于概率的交叉操作%%%%%%%%%%%%%%%
    for i=1:2:NP
        p = rand;
        if p < Pc
            q = randi(1,1,L);
            for j = 1:L
                if q(j)==1;
                    temp = nf(i+1,j);
                    nf(i+1,j) = nf(i,j);
                    nf(i,j) = temp;
                end
            end
        end
    end
    %%%%%%%%%%%%%%%基于概率的变异操作%%%%%%%%%%%%%%%
    i= 1;
    while i<= round(NP*Pm)
        h = randi([1,NP]);
        for j = 1:round(L*Pm)
            g = randi([1,L]);
            nf(h,g) =~ nf(h,g);
        end
        i=i+1;
    end
    f=nf;
    f(1,:) = fBest;
    trace(k) = maxFit;
end
xBest;
fBestt=func1(xBest);
subplot(1,2,1)
plot(trace)
xlabel(‘迭代次数‘)
ylabel(‘目标函数值‘)
title(‘适应度进化曲线‘)
subplot(1,2,2)
fplot(@(x)(10.*cos(5.*x.*x)+7.*sin(x-5)+10.*x.*x),[-1 0]);
hold on;
plot(xBest,func1(xBest),‘*‘);
%%%%%%%%%%%%%%%适应度函数%%%%%%%%%%%%%%%
function result = func1(x)
%fit = x+10*sin(5*x)+7*cos(4*x);
fit = 10.*cos(5.*x.*x)+7.*sin(x-5)+10.*x.*x;
result = fit;
end

1)运行结果

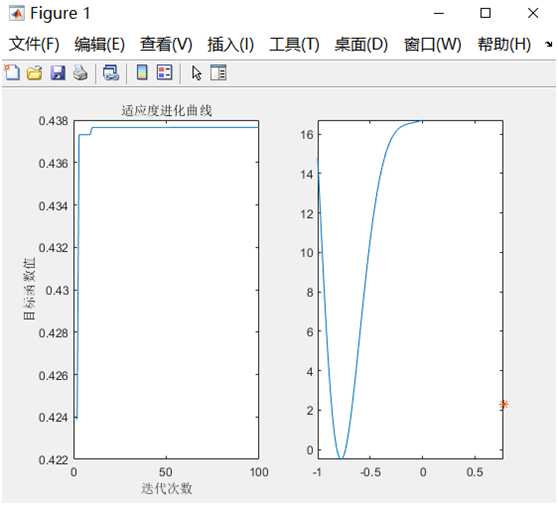
                                 适应度曲线

                                  函数图像

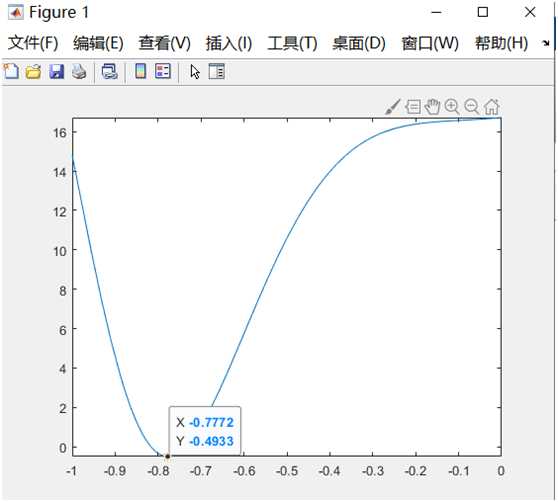
基于Matlab用遗传算法求一元函数最值问题（附源码）

标签：数值   遗传算法   参数   操作   pre   进制   问题   要求   val   

原文地址：https://www.cnblogs.com/Horizon-asd/p/12716735.html