标签:最短时间 img 邻居 str 最短路 png code 理念 假设
广度优先搜索找出的是段数最少的路径 而狄克斯特拉算法可以找出最快的路径
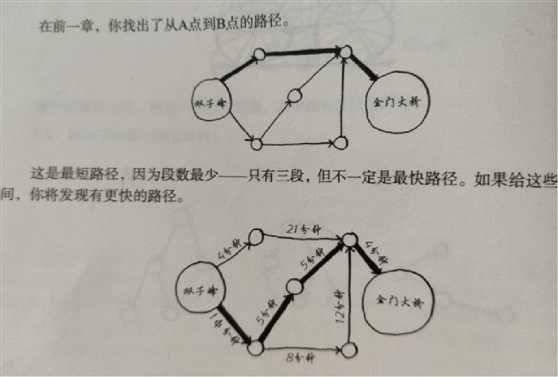

①找出最便宜的节点。比如说到A节点6分钟,到B节点2分钟【未明确前往终点的时间,假设无穷大】,所以节点B是最近的。
②计算经节点B前往各个邻居所需的时间,B-->A ,五分钟,更短! 直接到A需要6分钟。 对于节点B的邻居,如果前往它的更短路径,就更新其开销,
在这里就有前往A的更短路径,前往终点的更短路径,无穷大缩短为7分钟。
③重复第一步:找出刻在最短时间内前往的节点,除了节点B外就是 节点A。 然后更新节点A的所有邻居的开销 此时你发现前往终点时间为6分钟!更短了!
故:前往节点B 2分钟 ,再到A五分钟,最后到终点6分钟。
计算最终路径之后介绍,这就是最终路径【总权重最小】
注意:无向图中 ,A->B 与 B->A 等价 而有环的就肯定不会是最短路径 所以狄克斯特拉算法只适用于有向无环图。
另一种思考角度:从家里去单位,家到停车场6分钟,走经过学校2分钟,再到停车场1分钟。
如果走经过停车场的路去学校,能不能把时间缩短到少于2分钟呢?不可能。
另一方面,有没有最快到停车场的路?有。
狄克斯特拉算法背后的关键理念:找出图中最便宜的节点,并确保没有到该节点的更便宜的路径。
狄克斯特拉算法缺陷: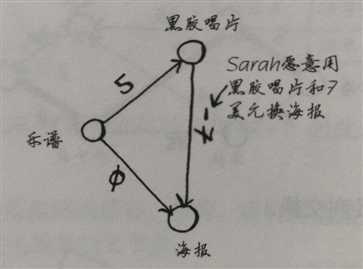
当使用狄克斯特拉算法时, 算法会认为没有比不花钱 更便宜的了。 但其实还有负权边这么一个概念。
狄克斯特拉算法不适用于包含负权边的图,要找出最短路径,可以使用贝尔曼-福德算法,这个待日后继续了解。
标签:最短时间 img 邻居 str 最短路 png code 理念 假设
原文地址:https://www.cnblogs.com/zhangshengchao/p/12732354.html