标签:粒子 简单的 基本算法 假设 turn numpy 测试结果 random 优化
粒子群算法(Particle Swarm Optimization,PSO)由Kennedy和Eberhart于1995年提出。该算法的思想来源于对鸟类捕食行为的研究,鸟之间通过集体的协作使得群体能够找到最多的食物,PSO便是通过模拟鸟群飞行觅食的行为,来寻找最优解的算法,这是一种基于群体智能(Swarm Intelligence)的优化方法。
在粒子群算法中,我们将鸟群抽象成粒子群,用一个粒子来代表一只鸟。PSO目标就是:通过一群粒子在解空间中进行搜索,找到使得适应度函数(fitness function)取得最大值(或最小值)的解。
在正式介绍算法前,先约定好一些符号。假设粒子在\(d\)维空间中进行搜索,种群大小为N(一共有N个粒子),适应度函数为\(f(\cdot)\)。
那么第\(i\)个粒子位置更新公式为:
其中
从更新公式可以看出,粒子下一时刻的运动速度收到三个因素的影响:当前时刻的速度、当前自己找到的最优解的位置以及当前全局最优解的位置。可以用一个图表示粒子位置的更新过程:
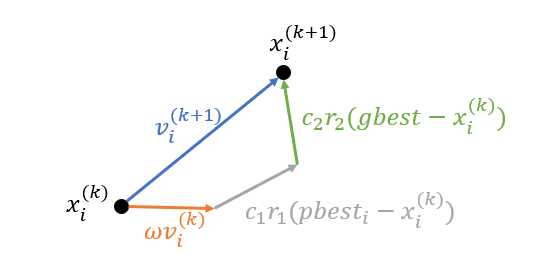
基本算法描述如下:
算法的停止条件:
这里我们PSO算法来搜索ackley函数的最小值,ackley函数是一个具有非常多个局部极小值的函数,具体表达式如下:
通常取\(a=20,b=0.2,c=2\pi\)。其中\(d\)表示空间的维数,即\(x\in\mathbb{R}^d\)。该函数具有全局最小值\(f(x^*)=0,x^*=0\)。函数图像如下(三维空间):
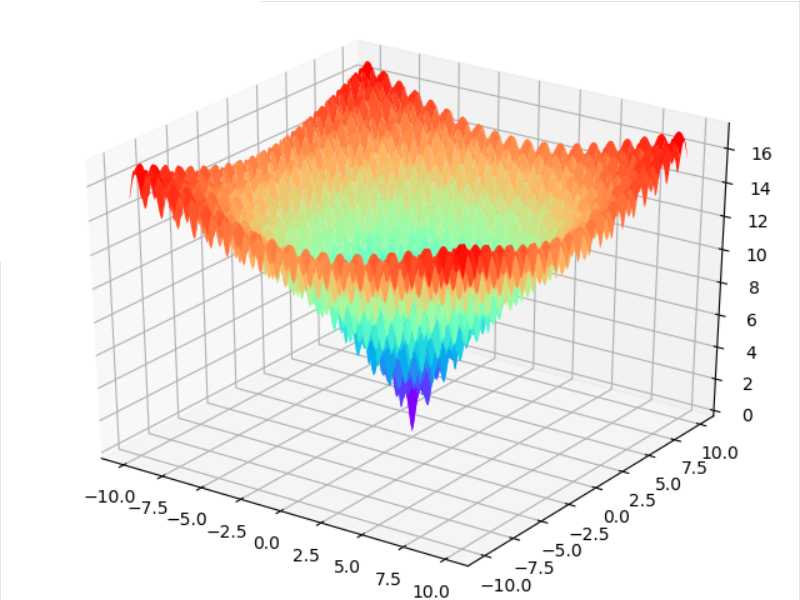
实现代码:
import numpy as np
# v(k+1) = w*v(k) + c1*r1*(gbest-x) + c2*r2*(pbest-x)
# x(k+1) = x(k) + v(k+1)
class Particle:
"""
st_x:位置约束,粒子每个维度上的坐标范围必须处于[st_x[0], st_x[1]]之间
st_v:速度约束,粒子每个维度上的速度范围必须处于[st_v[0], st_v[1]]之间
position:粒子的当前位置
velocity:粒子的当前速度
pbest:粒子自身历史记录的最佳位置
pvalue:粒子自身历史记录的最佳值
"""
st_x = None
st_v = None
def __init__(self, x, v, pbest, pvalue):
self.position = x
self.velocity = v
self.pbest = pbest
self.pvalue = pvalue
def update_velocity(self, v):
v[v < self.st_v[0]] = self.st_v[0]
v[v > self.st_v[1]] = self.st_v[1]
self.velocity = v
def update_position(self, func):
# 更新粒子自身的位置,以及判断是否要更新pbest
self.position += self.velocity
self.position[self.position < self.st_x[0]] = self.st_x[0]
self.position[self.position > self.st_x[1]] = self.st_x[1]
if self.pvalue > func(self.position):
self.pvalue = func(self.position)
self.pbest = self.position.copy()
class PSO:
"""
gbest:粒子群历史记录的最佳位置
gvalue:粒子群历史记录的最佳值
"""
gbest = None
gvalue = np.inf
def __init__(self, n_dims, n_particles, st_x, st_v, w, c1, c2, num_iter, func):
# 初始化空间维度
self.n_dims = n_dims
# 初始化粒子群数目
self.n_particles = n_particles
# 目标函数
self.func = func
# 粒子惯性权重
self.w = w
# 全局部分学习率
self.c1 = c1
# 自我认知部分学习率
self.c2 = c2
# 迭代次数
self.num_iter = num_iter
# 存放粒子群的列表(容器)
self.particles = []
# 初始化粒子的位置和速度约束
Particle.st_x = st_x
Particle.st_v = st_v
# 初始化粒子群
for _ in range(n_particles):
# 初始化粒子的随机位置在 st_x[0]~st_x[1]
x = (st_x[1] - st_x[0]) * np.random.rand(n_dims) + st_x[0]
# 计算当前评估值
pvalue = func(x)
# 初始化一个粒子
self.particles.append(
Particle(
x=x,
v=(st_v[1] - st_v[0]) * np.random.rand(n_dims) + st_v[0],
pbest=x.copy(),
pvalue=pvalue
)
)
if self.gvalue > pvalue:
self.gvalue = pvalue
self.gbest = x.copy()
def solve(self):
# 开始迭代
for index in range(1, self.num_iter + 1):
for particle in self.particles:
v = self.w * particle.velocity + self.c1 * np.random.rand() * (self.gbest - particle.position) + self.c2 * np.random.rand() * (particle.pbest - particle.position)
particle.update_velocity(v)
particle.update_position(self.func)
for particle in self.particles:
if particle.pvalue < self.gvalue:
self.gvalue = particle.pvalue
self.gbest = particle.pbest.copy()
return self.gbest, self.gvalue
def ackley(x):
return - 20 * np.exp(-0.2 * np.sqrt((x * x).mean())) - np.exp(np.cos(2 * np.pi * x).mean()) + 20 + np.exp(1)
if __name__ == "__main__":
# 测试不同迭代次数搜索出来的最优解情况
for i in range(11):
pso = PSO(
n_dims=10,
n_particles=100,
st_x=(-20, 20),
st_v=(-1, 1),
w=0.8,
c1=2,
c2=2,
num_iter=50 * i,
func=ackley
)
gbest, gvalue = pso.solve()
print("number of interations:%d\tgvalue:%f" % (50 * i, gvalue))
测试结果:
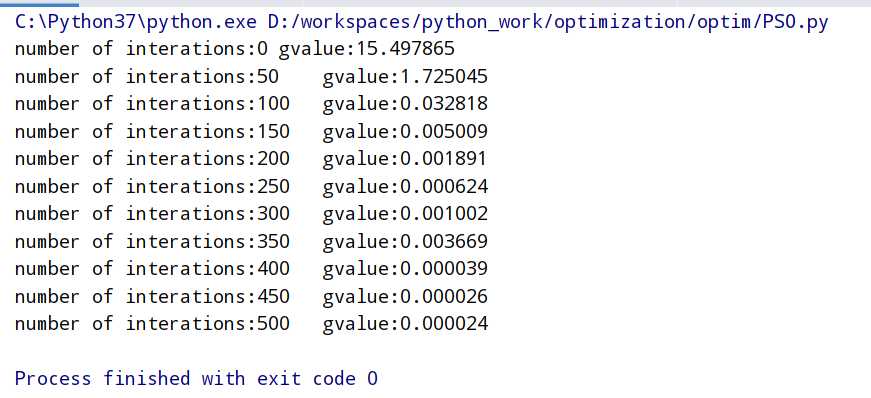
可以看到随着迭代次数的增加,所搜索到的最优解基本上都是越来越小的。大多数情况下都是这样的,不排除个别情况下,迭代次数多,反而找到更差的解。还需要注意的是当搜索空间维数太高,或者搜索区域很大的时候,粒子数太少往往很难找到全局最优解。但是如果增加粒子数,增加迭代次数提高算法搜索能力,又需要很大的时间开销。
标签:粒子 简单的 基本算法 假设 turn numpy 测试结果 random 优化
原文地址:https://www.cnblogs.com/philolif/p/PSO.html