标签:指针 ash 否则 bsp tab alpha 关键字 地址 数据
哈希是通过对数据进行再压缩,提高效率的一种解决方法。但由于通过哈希函数产生的哈希值是有限的,而数据可能比较多,导致经过哈希函数处理后仍然有不同的数据对应相同的哈希值。这时候就产生了哈希冲突。
开放地址法;再哈希法;链地址法(拉链法);公共溢出区法。
开放地址法处理冲突的基本原则就是出现冲突后按照一定算法查找一个空位置存放。公式:
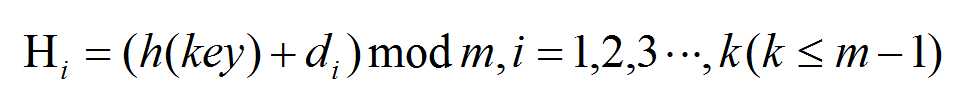
其中:Hi为计算出的地址,h(key)为哈希方法,di增量序列1,2,3,...,k(k<= m - 1),m为哈希表的长度。
假设问题:关键码集合为:{38,25,74,63,52,48,55},m = 7,采用除留余数法h(key) = key mod 7,并存储在哈希表中。

![]()
从上图可以看出,38和52存放3号地址冲突,25和74存放4地址冲突,根据集合,可以知道,38先存放在了3,25先存放了4,所以将74和52进行线上探测,根据公式,线上探测74时,取d = 1,探测52时,取d = 5,最终结果如下表:

优点:只要哈希表未被填满,保证能找到一个空地址单元存放有冲突的元素。
缺点:能使第i个哈希地址的同义词存入第i+1个地址,这样本应存入第i+1个哈希地址的元素变成了第i+2个哈希地址的同义词,产生“聚集”现象,降低查找效率。
![]()
以上面(一)线上探测74为例,根据公式,取d = 1²,最终结果如下表:

还是以74为例,根据公式,取d = 29时,最终结果如下表:

1、取数据元素的关键码key,计算其哈希函数值(地址)。若该地址对应的存储 空间还没有被占用,则将该元素存入;否则执行2解决冲突。
2、根据选择的冲突处理方法,计算关键码key的下一个存储地址。若下一个存储地址仍被占用,则继续执行2,直到找到能用的存储地址为止。
再哈希法,又叫双哈希法,有多个不同的Hash函数,出现冲突后采用其他的哈希函数计算,直到不再冲突为止。虽然不易发生聚集,但是增加了计算时间。公式:
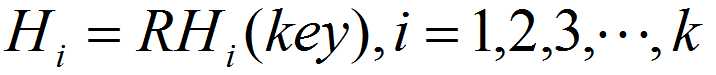
其中RHi为不同的哈希函数。比如乘余取整法:RH(k)=[b ×(a × k mod 1)] ,还是以上面74为例:设b = 10,a = 0.6180339,根据公式有:RH(74)=[10 ×(0.6180339 × 74 mod 1)] = 7,最终结果如下表:

将具有相同哈希地址的记录链成一个单链表,m个哈希地址就设m个单链表,,然后用一个数组将m个单链表的表头指针存储起来,形成一个动态的结构。
优点:
1、拉链法处理冲突简单,且无堆积现象,即非同义词决不会发生冲突,因此平均查找长度较短;
2、由于拉链法中各链表上的结点空间是动态申请的,故它更适合于造表前无法确定表长的情况;
3、开放定址法为减少冲突,要求装填因子α较小,故当结点规模较大时会浪费很多空间。而拉链法中可取α≥1,且结点较大时,拉链法中增加的指针域可忽略不计,因此节省空间;
4、在用拉链法构造的散列表中,删除结点的操作易于实现。只要简单地删去链表上相应的结点即可。
缺点:
1、指针占用较大空间时,会造成空间浪费,若空间用于增大散列表规模进而提高开放地址法的效率。
假设:关键字集合{47,7,29,11,16,92,22,8,3,50,37,89},m = 11,哈希算法为H(k) = k mod 11,则建表如下图:
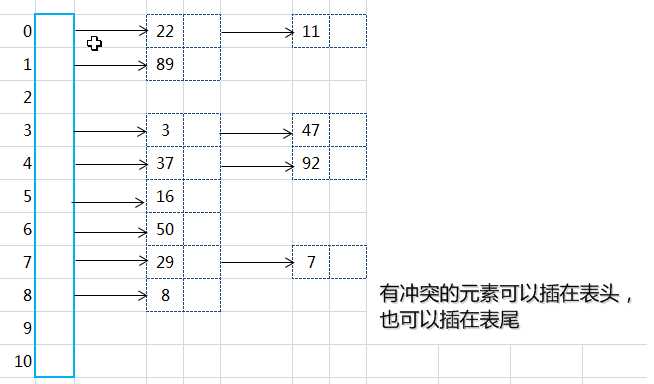
1、取数据元素的关键码key,计算其哈希函数值(地址)。若该地址对应的链表为空,则将该元素插入此链表;否则执行2解决冲突。
2、根据选择的冲突处理方法,计算关键码key的下一个存储地址。若该地址对应的链表不为空,则利用链表的前插法或后插法将该元素插入此链表。
1、非同义词不会冲突,无“聚集”现象;
2、链表上的结点空间动态申请,适用于表长不确定的情况。
创建哈希表时,将所有产生冲突的的同义词集中放在一个溢出表中。假设哈希函数的值域是[1,m-1],则设哈希表HashTable[0...m-1]为基本表,每个分量存放一个记录,另外设溢出表OverTable[0,v]为溢出表,所有关键字和基本表中关键字为同义词的记录,不管它们由哈希函数得到的哈希地址是什么,一旦发生冲突,都填入溢出表。
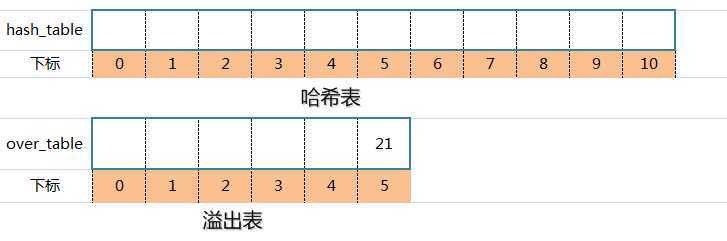
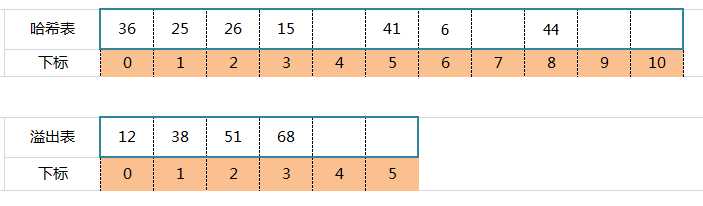
例子:关键码集合{26,36,41,38,44,15,68,12,6,51,25},m = 12,哈希函数:H(k)= k mod 12,则哈希表如下:

上图蓝色部分,元素的哈希地址冲突了,此时创建一个溢出表:
标签:指针 ash 否则 bsp tab alpha 关键字 地址 数据
原文地址:https://www.cnblogs.com/lingq/p/12761837.html