标签:观察 归一化 速度 特征 支持 约束 概念 参考 alpha
在分离超平面固定为\(w^Tx+b=0\)的时候,\(|w^Tx+b|\)表示点x到超平面的相对距离。通过观察\(w^Tx+b\)和\(y\)是否同号,判断分类是否正确,引入函数间隔的概念,定义函数间隔\(γ′\)为:
可以看到,它就是感知机模型里面的误分类点到超平面距离的分子。对于训练集中m个样本点对应的m个函数间隔的最小值,就是整个训练集的函数间隔。
函数间隔并不能正常反应点到超平面的距离,在感知机模型里我们也提到,当分子成比例的增长时,分母也是成倍增长。为了统一度量,我们需要对法向量w加上约束条件,这样我们就得到了几何间隔\(γ\),定义为:
几何间隔才是点到超平面的真正距离,感知机模型里用到的距离就是几何距离。
在感知机模型中,我们可以找到多个可以分类的超平面将数据分开,并且优化时希望所有的点都被准确分类。但是实际上离超平面很远的点已经被正确分类,它对超平面的位置没有影响。我们最关心是那些离超平面很近的点,这些点很容易被误分类。如果我们可以让离超平面比较近的点尽可能的远离超平面,最大化几何间隔,那么我们的分类效果会更好一些。SVM的思想起源正起于此。
如下图所示,分离超平面为\(w^Tx+b=0\),如果所有的样本不光可以被超平面分开,还和超平面保持一定的函数距离(下图函数距离为1),那么这样的分类超平面是比感知机的分类超平面优的。可以证明,这样的超平面只有一个。和超平面平行的保持一定的函数距离的这两个超平面对应的向量,我们定义为支持向量,如下图虚线所示。
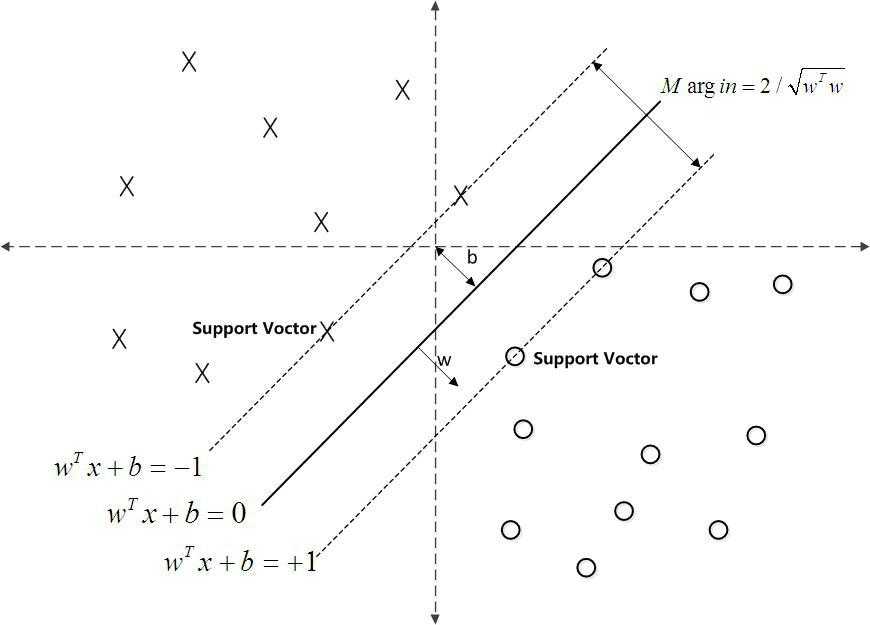
SVM的模型是让所有点到超平面的距离大于一定的距离,也就是所有的分类点要在各自类别的支持向量两边。用数学式子表示为:
一般我们都取函数间隔γ′为1,这样我们的优化函数定义为:
也就是说,我们要在约束条件\(yi(wTxi+b)≥1(i=1,2,...m)\)下,最大化\(\frac{1}{||w||2}\)。可以看出,这个感知机的优化方式不同,感知机是固定分母优化分子,而SVM是固定分子优化分母,同时加上了支持向量的限制。
由于\(\frac{1}{||w||2}\)的最大化等同于\(\frac{1}{2}||w||_2^2\)的最小化。这样SVM的优化函数等价于:
由于目标函数\(\frac{1}{2}||w||_2^2\)是凸函数,同时约束条件不等式是仿射的,根据凸优化理论,我们可以通过拉格朗日函数将我们的优化目标转化为无约束的优化函数。具体的,优化函数转化为:
由于引入了朗格朗日乘子,我们的优化目标变成:
优化函数满足KKT条件,也就是说,我们可以通过拉格朗日对偶将我们的优化问题转化为等价的对偶问题来求解。
也就是说,现在我们要求的是:
从上式中,我们可以先求优化函数对于w和b的极小值。接着再求拉格朗日乘子α的极大值。
首先我们来求L(w,b,α)基于w和b的极小值,即\(\underbrace{min}_{w,b}\,L(w, b, a)\)。这个极值我们可以通过对w和b分别求偏导数得:
从上两式子可以看出,我们已经求得了w和α的关系,只要我们后面接着能够求出优化函数极大化对应的α,就可以求出我们的w了,至于b,由于上两式已经没有b,所以最后的b可以有多个。
既然我们已经求出w和α的关系,就可以带入优化函数\(L(w, b, a)\)消去w了。我们定义:
现在我们来看将w替换为α的表达式以后的优化函数\(ψ(α)\)的表达式:
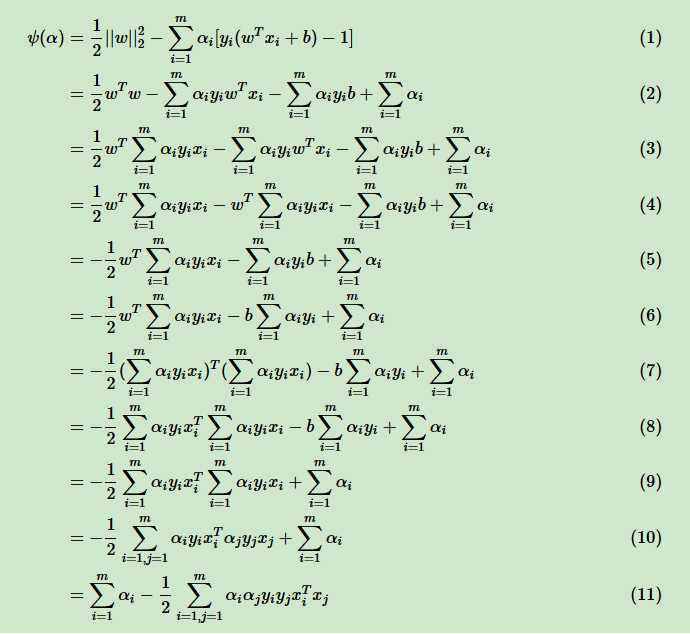


| 参数 | LinearSVC | SVC | NuSVC |
|---|---|---|---|
| 惩罚系数C | 即为我们第二节中SVM分类模型原型形式和对偶形式中的惩罚系数C,默认为1,一般需要通过交叉验证来选择一个合适的C。一般来说,如果噪音点较多时,C需要小一些。 | NuSVC没有这个参数, 它通过另一个参数nu来控制训练集训练的错误率,等价于选择了一个C,让训练集训练后满足一个确定的错误率 | |
| nu | LinearSVC 和SVC没有这个参数,LinearSVC 和SVC使用惩罚系数C来控制惩罚力度。 | nu代表训练集训练的错误率的上限,或者说支持向量的百分比下限,取值范围为(0,1],默认是0.5.它和惩罚系数C类似,都可以控制惩罚的力度。 | |
| 核函数 kernel | LinearSVC没有这个参数,LinearSVC限制了只能使用线性核函数 | 核函数有四种内置选择,第三节已经讲到:‘linear’即线性核函数, ‘poly’即多项式核函数, ‘rbf’即高斯核函数, ‘sigmoid’即sigmoid核函数。如果选择了这些核函数, 对应的核函数参数在后面有单独的参数需要调。默认是高斯核‘rbf‘。 还有一种选择为"precomputed",即我们预先计算出所有的训练集和测试集的样本对应的Gram矩阵,这样K(x,z) 直接在对应的Gram矩阵中找对应的位置的值。 当然我们也可以自定义核函数, 由于我没有用过自定义核函数,这里就不多讲了。 | |
| 正则化参数penalty | 仅仅对线性拟合有意义,可以选择‘l1’即L1正则化 或者 ‘l2’即L2正则化。默认是L2正则化,如果我们需要产生稀疏话的系数的时候,可以选L1正则化,这和线性回归里面的Lasso回归类似。 | SVC和NuSVC没有这个参数 | |
| 是否用对偶形式优化dual | 这是一个布尔变量,控制是否使用对偶形式来优化算法,默认是True,即采用上面第二节的分类算法对偶形式来优化算法。如果我们的样本量比特征数多,此时采用对偶形式计算量较大,推荐dual设置为False,即采用原始形式优化 | SVC和NuSVC没有这个参数 | |
| 核函数参数degree | LinearSVC没有这个参数,LinearSVC限制了只能使用线性核函数 | 如果我们在kernel参数使用了多项式核函数 ‘poly‘,那么我们就需要对这个参数进行调参。这个参数对应K(x,z)=(γx?z+r)d中的d。默认是3。一般需要通过交叉验证选择一组合适的γ,r,d | |
| 核函数参数gamma | LinearSVC没有这个参数,LinearSVC限制了只能使用线性核函数 | 如果我们在kernel参数使用了多项式核函数 ‘poly‘,高斯核函数‘rbf’, 或者sigmoid核函数,那么我们就需要对这个参数进行调参。多项式核函数中这个参数对应K(x,z)=(γx?z+r)d 中的γ。一般需要通过交叉验证选择一组合适的γ,r,d高斯核函数中这个参数对应K(x,z)=exp(?γ||x?z||2) 中的γ。一般需要通过交叉验证选择合适的γsigmoid核函数中这个参数对应K(x,z)=tanh(γx?z+r)中的γ。一般需要通过交叉验证选择一组合适的γ,r γ默认为‘auto‘,即1特征维度 | |
| 核函数参数coef0 | LinearSVC没有这个参数,LinearSVC限制了只能使用线性核函数 | 如果我们在kernel参数使用了多项式核函数 ‘poly‘,或者sigmoid核函数,那么我们就需要对这个参数进行调参。多项式核函数中这个参数对应K(x,z)=(γx?z+r)d 中的r。一般需要通过交叉验证选择一组合适的γ,r,dsigmoid核函数中这个参数对应K(x,z)=tanh(γx?z+r)中的r。一般需要通过交叉验证选择一组合适的γ,r coef0默认为0 | |
| 样本权重class_weight | 指定样本各类别的的权重,主要是为了防止训练集某些类别的样本过多,导致训练的决策过于偏向这些类别。这里可以自己指定各个样本的权重,或者用“balanced”,如果使用“balanced”,则算法会自己计算权重,样本量少的类别所对应的样本权重会高。当然,如果你的样本类别分布没有明显的偏倚,则可以不管这个参数,选择默认的"None" | ||
| 分类决策decision_function_shape | LinearSVC没有这个参数,使用multi_class参数替代。 | 可以选择‘ovo‘或者‘ovo’.目前0.18版本默认是‘ovo‘.0.19版本将是‘ovr‘ OvR(one ve rest)的思想很简单,无论你是多少元分类,我们都可以看做二元分类。具体做法是,对于第K类的分类决策,我们把所有第K类的样本作为正例,除了第K类样本以外的所有样本都作为负例,然后在上面做二元分类,得到第K类的分类模型。其他类的分类模型获得以此类推。OvO(one-vs-one)则是每次每次在所有的T类样本里面选择两类样本出来,不妨记为T1类和T2类,把所有的输出为T1和T2的样本放在一起,把T1作为正例,T2作为负例,进行二元分类,得到模型参数。我们一共需要T(T-1)/2次分类。从上面的描述可以看出OvR相对简单,但分类效果相对略差(这里指大多数样本分布情况,某些样本分布下OvR可能更好)。而OvO分类相对精确,但是分类速度没有OvR快。一般建议使用OvO以达到较好的分类效果。 | |
| 分类决策multi_class | 可以选择 ‘ovr’ 或者 ‘crammer_singer’ ‘ovr’和SVC和nuSVC中的decision_function_shape对应的‘ovr’类似。‘crammer_singer‘是一种改良版的‘ovr‘,说是改良,但是没有比’ovr‘好,一般在应用中都不建议使用。 | SVC和nuSVC没有这个参数,使用decision_function_shape参数替代 | |
| 缓存大小cache_size | LinearSVC计算量不大,因此不需要这个参数 | 在大样本的时候,缓存大小会影响训练速度,因此如果机器内存大,推荐用500MB甚至1000MB。默认是200,即200MB. | |
| 参数 | LinearSVR | SVR | nuSVR |
|---|---|---|---|
| 惩罚系数C | 即为我们第二节中SVM分类模型原型形式和对偶形式中的惩罚系数C,默认为1,一般需要通过交叉验证来选择一个合适的C。一般来说,如果噪音点较多时,C需要小一些。大家可能注意到在分类模型里面,nuSVC使用了nu这个等价的参数控制错误率,就没有使用C,为什么我们nuSVR仍然有这个参数呢,不是重复了吗?这里的原因在回归模型里面,我们除了惩罚系数C还有还有一个距离误差?来控制损失度量,因此仅仅一个nu不能等同于C.也就是说回归错误率是惩罚系数C和距离误差?共同作用的结果。后面我们可以看到nuSVR中nu的作用。 | ||
| nu | LinearSVR 和SVR没有这个参数,用?控制错误率 | nu代表训练集训练的错误率的上限,或者说支持向量的百分比下限,取值范围为(0,1],默认是0.5.通过选择不同的错误率可以得到不同的距离误差?。也就是说这里的nu的使用和LinearSVR 和SVR的?参数等价。 | |
| 距离误差epsilon | 即我们第二节回归模型中的?,训练集中的样本需满足???ξ∨i≤yi?w??(xi)?b≤?+ξ∧i | nuSVR没有这个参数,用nu控制错误率 | |
| 是否用对偶形式优化dual | 和SVC类似,可参考上一节的dual描述 | SVR和NuSVR没有这个参数 | |
| 正则化参数penalty | 和SVC类似,可参考上一节的penalty 描述 | SVR和NuSVR没有这个参数 | |
| 核函数 kernel | LinearSVR没有这个参数,LinearSVR限制了只能使用线性核函数 | 和SVC, nuSVC类似,可参考上一节的kernel描述 | |
| 核函数参数degree, gamma 和coef0 | LinearSVR没有这些参数,LinearSVR限制了只能使用线性核函数 | 和SVC, nuSVC类似,可参考上一节的kernel参数描述 | |
| 损失函数度量loss | 可以选择为‘epsilon_insensitive’ 和 ‘squared_epsilon_insensitive’ ,如果选择‘epsilon_insensitive’ ,则损失度量满足???ξ∨i≤yi?w??(xi)?b≤?+ξ∧i,即和第二节的损失度量一样。是默认的SVM回归的损失度量标准形式。如果选择为 ‘squared_epsilon_insensitive’ , 则损失度量满足(yi?w??(xi)?b)2≤?+ξi,此时可见会少一个松弛系数。其优化过程我们在SVM原理系列里没有讲,但是目标函数优化过程是完全相似的。 一般用默认的‘epsilon_insensitive’就足够了。 | SVR和NuSVR没有这个参数 | |
| 缓存大小cache_size | LinearSVC计算量不大,因此不需要这个参数 | 在大样本的时候,缓存大小会影响训练速度,因此如果机器内存大,和SVC,nuSVC一样,推荐用500MB甚至1000MB。默认是200,即200MB. | |
标签:观察 归一化 速度 特征 支持 约束 概念 参考 alpha
原文地址:https://www.cnblogs.com/54hys/p/12813784.html