标签:sea template 排列 == node 结构 中序 src 使用
二叉排序树是为了实现数据的有序排列,并可方便的对树中的数据进行插入和删除操作,提高查找效率。
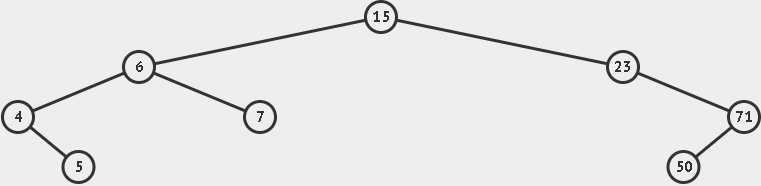
性质:
下面说说二叉排序树的查找,插入,删除操作实现。
二叉排序树的结点结构:
template<class T>
class BTNode
{
public:
//数据域
T data;
//指针域
BTNode<T> *lchild,*rchild;
public:
//构造函数
BTNode(T D,BTNode<T> *l = NULL,BTNode<T> *r=NULL) : data(D),lchild(l),rchild(r) {}
};
二叉排序树是一个有序的二叉树,其左子树永远比根节点的值小,右子树用于比根节点的值大。因此我们可以使用递归技术,如果key<p->data,则在p的左子树里面继续寻找;若key>p->data则在p的右子树里面继续寻找;直到key=p->data;否则表示未搜索到,退出函数。实现过程如下图:
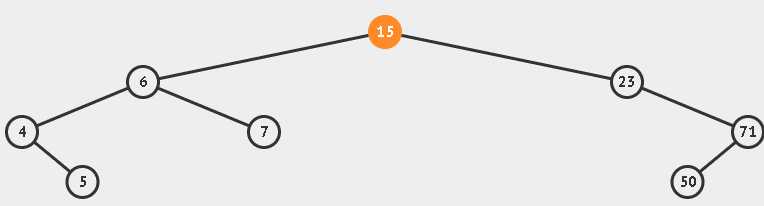
代码实现
/*
1、在rt中递归查找key是否存在,若不存在返回false
2、f指向rt结点的双亲,若rt为根节点,则f=NULL
3、若key存在,则返回true,p指向该数据值为key的结点
4、若key不存在,返回false,p指向访问的最后一个节点
*/
bool SearchBST(BTNode<T> *rt, T key, BTNode<T> *&p = NULL, BTNode<T> *f = NULL)
{
if (!rt) //查找失败
{
p = f;
return false;
}
else if (key == rt->data) //查找成功
{
p = rt;
return true;
}
else if (key > rt->data)
{
return SearchBST(rt->rchild, key, p, rt); //在右子树继续查找
}
else
{
return SearchBST(rt->lchild, key, p, rt); //在左子树继续查找
}
}
收获:函数的参数列表若有指针,并且调用函数时,用的就是一个指针进行传递,则进行的是值传递。而*&a可以避免这种现象,这时进行的是地址传递。
插入的关键是,在插入元素后还要继续保持二叉树的有序性。实现过程如下图:
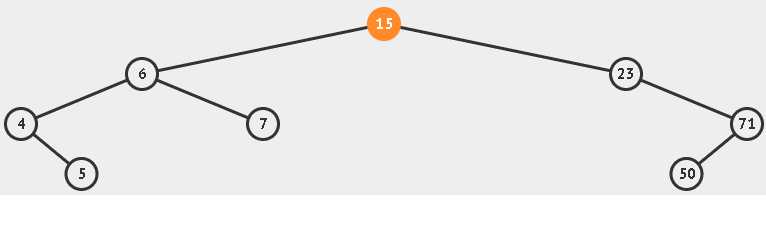
代码实现:
/*
1、先搜索二叉树rt中是否存在值key
2、若存在则返回false,不存在则插入
*/
bool Insert(BTNode<T> *&rt, T key)
{
BTNode<T> *p = NULL;
if (!this->SearchBST(rt, key, p))//未存在key
{
BTNode<T> *s = new BTNode<T>(key, NULL, NULL);
if (!p)//p为空,即根节点为空
{
rt = s;//令根结点等于s
}
else if (key < p->data)
{
p->lchild = s;//key小于p->data,将p的左孩子置为s
}
else
{
p->rchild = s;//key大于p->data,将p的右孩子置为s
}
return true;
}
else
{
return false;
}
}
二叉排序树的难点是删除操作。
删除结点分三种情况:
结点没有左右孩子:
解决办法:删除该结点,将该结点的双亲指针域置为NULL
结点只有左子树或右子树:
解决办法:删除该结点,将该结点的双亲指针域指向该结点的左子树或右子树。
结点左右子树均有:
解决办法:保留该结点,将该结点的数据域改为该结点直接前驱(或直接后继)结点的值,删除该结点的直接前驱结点。
实现过程如下图:
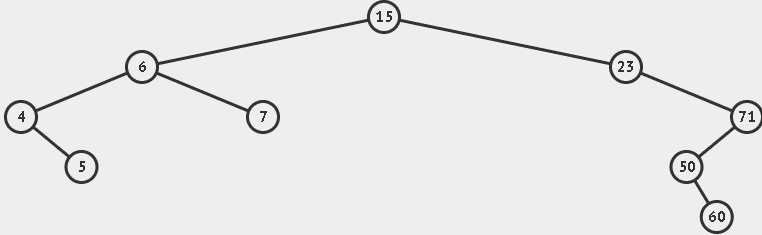
代码实现:
/*
若二叉树rt中存在key,在删除结点,并返回true,否则返回false
*/
bool DeleteBST(BTNode<T> *&rt,T key)//地址传递
{
if(!rt)
{
//未找到
return false;
}
else
{
if(rt->data==key)
{
//找到key
return Delete(rt);//rt只是其双亲指针域的一个别名
}
else if (rt->data>key)
{
return DeleteBST(rt->lchild,key);
}
else
{
return DeleteBST(rt->rchild,key);
}
}
}
Delete函数实现:
bool Delete(BTNode<T> *&p)//地址传递,p只是别名
{
BTNode<T> *q;
//只存在右子树,或右子树也不存在
if(!p->lchild)
{
q=p;
p=p->rchild;//重接其右子树
delete q;//删除原来的结点
}
//只存在左子树
else if (!p->rchild)
{
q=p;
p=p->lchild;
delete q;
}
//左右子树均存在
else
{
BTNode<T> *s=p;
q=p->lchild;
//寻找其直接前驱结点
while(q->rchild)
{
s=q;//s为q的双亲
q=q->rchild;
}
//将q的值赋给p
p->data=q->data;
if(s!=p)//若p和q的双亲指向不等
{
s->rchild=q->lchild;//重接s的右子树
}
else
{
s->lchild=q->lchild;//重接s的左子树
}
delete q;
}
return true;
}
C++代码实现:
#include <iostream>
using namespace std;
//二叉树结点
template <class T>
struct BTNode
{
T data; //存储数据
BTNode<T> *lchild, *rchild; //左右孩子指针
BTNode(T D, BTNode<T> *l = NULL, BTNode<T> *r = NULL) : data(D), lchild(l), rchild(r) {}
};
//二叉树
template <class T>
class BST
{
//属性值
private:
//根节点指针
BTNode<T> *root;
//查找结点
bool SearchBSTP(BTNode<T> *rt, T key, BTNode<T> *&p = NULL, BTNode<T> *f = NULL)
{
if (!rt) //查找失败
{
p = f;
return false;
}
else if (key == rt->data) //查找成功
{
p = rt;
return true;
}
else if (key > rt->data)
{
return SearchBSTP(rt->rchild, key, p, rt); //在右子树继续查找
}
else
{
return SearchBSTP(rt->lchild, key, p, rt); //在左子树继续查找
}
}
//插入结点
bool Insert(BTNode<T> *&rt, T key)
{
BTNode<T> *p = NULL;
if (!this->SearchBSTP(rt, key, p))
{
BTNode<T> *s = new BTNode<T>(key, NULL, NULL);
if (!p)
{
rt = s;
}
else if (key < p->data)
{
p->lchild = s;
}
else
{
p->rchild = s;
}
return true;
}
else
{
return false;
}
}
//删除结点
bool Delete(BTNode<T> *&p)
{
BTNode<T> *q;
if(!p->lchild)
{
q=p;
p=p->rchild;
delete q;
}
else if (!p->rchild)
{
q=p;
p=p->lchild;
delete q;
}
else
{
BTNode<T> *s=p;
q=p->lchild;
while(q->rchild)
{
s=q;
q=q->rchild;
}
p->data=q->data;
if(s!=p)
{
s->rchild=q->lchild;
}
else
{
s->lchild=q->lchild;
}
delete q;
}
return true;
}
bool DeleteBSTP(BTNode<T> *&rt,T key)
{
if(!rt)
{
//未找到
return false;
}
else
{
if(rt->data==key)
{
//找到key
return Delete(rt);
}
else if (rt->data>key)
{
return DeleteBSTP(rt->lchild,key);
}
else
{
return DeleteBSTP(rt->rchild,key);
}
}
}
//中序遍历
void InOrder(BTNode<T> *rt)
{
if(rt)
{
InOrder(rt->lchild);
cout<<rt->data<<" ";
InOrder(rt->rchild);
}
}
//删除二叉树
void Destory(BTNode<T> *&rt)
{
if(rt)
{
Destory(rt->lchild);
Destory(rt->rchild);
delete rt;
}
}
//行为属性
public:
//构造函数
BST(BTNode<T> *r = NULL) : root(r) {}
//拷贝构造函数
BST(const BST<T> &bt) : root(NULL)
{
}
//删除二叉树
void Destory()
{
this->Destory(this->root);
this->root=NULL;
}
//析构函数
~BST()
{
this->Destory();
}
//获得根指针
BTNode<T> *Getroot()
{
return this->root;
}
//搜索值
//并将
bool SearchBST(T key, BTNode<T> *p = NULL)
{
return this->SearchBSTP(this->root, key, p, NULL);
}
//插入结点,顺序插入
/*1、先判断此值是否存在,若存在,则返回true
2、若不存在,创造结点s,并顺序插入二叉树中
3、若不存在,则存在指针p指向查找路径的最后一个结点
4、判断插入值和指针p指向的值的大小,若key>p->data,则p->rchild=s;
否则p->lchild=s;
*/
bool InsertBST(T key)
{
return this->Insert(this->root, key);
}
//shanchujiedian
bool DeleteBST(T key)
{
return this->DeleteBSTP(this->root, key);
}
void InOrder()
{
this->InOrder(this->root);
}
};
int main()
{
BST<int> temp;
int a[] = {62,58,88,47,73,99,35,51,93,29,37,49,56,36,48,50};
for (int i = 0; i < 16; i++)
{
temp.InsertBST(a[i]);
}
temp.InOrder();
cout<<endl;
//BTNode<int> *p;
cout << "查找结果:" << temp.SearchBST(51) << endl;
temp.DeleteBST(62);
cout << "查找结果:" << temp.SearchBST(50) << endl;
temp.InOrder();
cout<<endl;
temp.Destory();
temp.InOrder();
cout<<endl;
system("pause");
return 0;
}
标签:sea template 排列 == node 结构 中序 src 使用
原文地址:https://www.cnblogs.com/cqy-wt1124/p/12818809.html