标签:growth 通过 不同的 parent str 抽取 http png +=
对于发现频繁项集,Apriori是一个很好的算法,但Apriori在发现频繁项集的时候需要多次扫描数据库,这严重影响了速度。
而FP-growth算法基于Apriori构建,不过在完成相同的发现频繁集的任务上,它采用了一些不同的技术。将数据集存储在一个特定的被称为FP树的结构之后去发现频繁项集。这种做法使得其只需对数据库进行两次扫描,从而大大提高了其发现频繁项集的速度。
FP-growth发现频繁项集的基本过程如下:
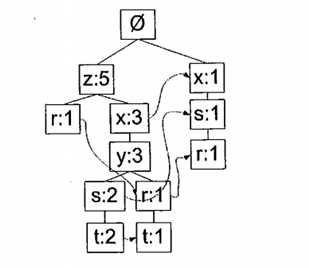
图 1 FP树是以下面的数据集构造成的
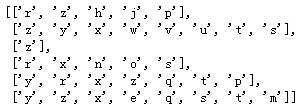
图2 数据集
要构造FP树,首先需要定义FP树的节点,
# fp树节点结构 class treeNode: def __init__(self,nameValue,numOccur,parentNode): self.name=nameValue self.count=numOccur self.nodeLink=None self.parent=parentNode self.children={} ? def inc(self,numOccur): self.count+=numOccur # 打印路径 def disp(self,ind=1): print(‘ ‘*ind,self.name,‘ ‘,self.count) for child in self.children.values(): child.disp(ind+1) |
为构建FP树,会扫描两遍数据库。
第一遍,对所有元素项出现的次数进行计数,去掉不满足最小支持度的元素项。
第二遍,构建FP树,FP树会存储项集的出现频率,而每个项集会以路径的方式存储在树中,存在相似元素的集合会共享树的一部分。只有当集合之间完全不相同时,树才会分叉。
为了构造FP树和挖掘频繁项集,还需要构造一个头指针表来辅助。
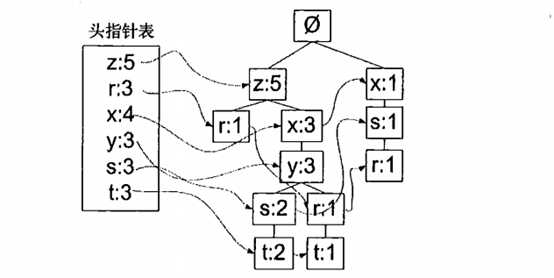
图3 带有头指针表的FP树
FP树的构造和构造辅助的头指针表实现如下
# FP树的构造 def createTree(dataSet,minSup=1): headerTable={} # 头指针表 for trans in dataSet: for item in trans: headerTable[item]=headerTable.get(item,0)+dataSet[trans] # 移除不满足最小支持度的元素项 for k in list(headerTable.keys()): if headerTable[k]<minSup: del(headerTable[k]) # 根据头指针表 建频繁元素项集 freqItemSet =headerTable.keys() if len(freqItemSet)==0: return None,None ? for k in headerTable: headerTable[k]=[headerTable[k],None] # 建立根节点 retTree = treeNode(‘Null Set‘,1,None) # 第二次扫描数据集,建立 FP 树, 并对事务中的频繁元素排序 for tranSet,count in dataSet.items(): localD={} for item in tranSet: if item in freqItemSet: localD[item]=headerTable[item][0] # 根据全局频率对事务中频繁元素项排序 if len(localD)>0: orderedItems=[v[0] for v in sorted(localD.items(), key=lambda p: p[1],reverse=True)] # 使用排序后的频繁项集对树进行填充 updateTree(orderedItems,retTree,headerTable,count) return retTree,headerTable ? def updateTree(items,inTree,headerTable,count): if items[0] in inTree.children: inTree.children[items[0]].inc(count) else: # 放入新的子节点 inTree.children[items[0]]=treeNode(items[0],count,inTree) if headerTable[items[0]][1]==None: headerTable[items[0]][1]=inTree.children[items[0]] else: # 更新头指针表的链接 updateHeader(headerTable[items[0]][1],inTree.children[items[0]]) if len(items)>1: updateTree(items[1::],inTree.children[items[0]],headerTable,count) ? def updateHeader(nodeToTest,targetNode): while(nodeToTest.nodeLink!=None): nodeToTest=nodeToTest.nodeLink nodeToTest.nodeLink=targetNode |
用图2 的数据集测试构造FP树
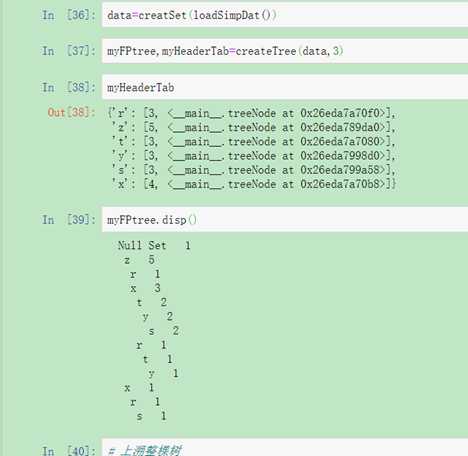
图4 测试构造FP树
有了FP树之后,就可以抽取频繁项集了。其思路大致和Apiori相似,首先从单个元素项开始,然后在此基础上逐步构建更大的集合。基本步骤如下:
# 挖掘频繁项集 def mineTree(inTree,headerTable,minSup,preFix,freqItems): bigL = [v[0] for v in sorted(headerTable.items(),key=lambda p :p[0])] for basePat in bigL: newFreqSet=preFix.copy() newFreqSet.add(basePat) ? # freqItems.append(newFreqSet) # freqItemSet 修改为字典结构,便于规则的发现生成 tmp=newFreqSet.copy() tmp=frozenset(tmp) freqItems[tmp]=headerTable[basePat][0] ? conPatBases=findPrefixPath(basePat,headerTable[basePat][1]) myCondTree,myHead=createTree(conPatBases,minSup) if myHead!=None: mineTree(myCondTree,myHead,minSup,newFreqSet,freqItems) ? # 上溯整棵树 def ascendTree(leafNode,prefixPath): if leafNode.parent!=None: prefixPath.append(leafNode.name) ascendTree(leafNode.parent,prefixPath) # 找出前缀路径 def findPrefixPath(basePat,treeNode): condPats={} while treeNode!=None: prefixPath=[] ascendTree(treeNode,prefixPath) if len(prefixPath)>1: condPats[frozenset(prefixPath[1:])]=treeNode.count treeNode=treeNode.nodeLink return condPats |
同样,利用上面的数据集,通过FP树挖掘出所有频繁项集
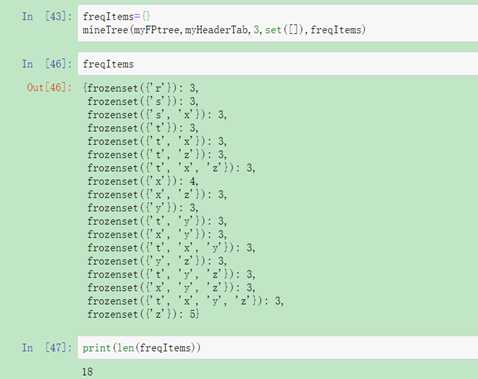
图5 挖掘出数据集的频繁项集
最后是利用所发现的频繁项集,发现生成出满足一定置信度的规则
# 从频繁项集中找出符合最小置信度的规则 def disp_rules(freqItems,minconf): n_rules=0 for item1,value1 in freqItems.items(): for item2,value2 in freqItems.items(): conf=value2/float(value1) if (item1 != item2) and (item1.issubset(item2)) and conf>minconf: print(item1,‘ --> ‘,(item2-item1),‘ conf:‘,conf) n_rules+=1 print(‘the number of total rules :‘,n_rules) disp_rules(freqItems,minconf=0.7) |
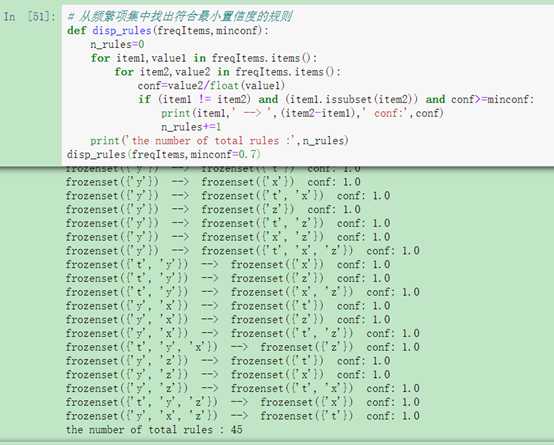
图6 根据频繁项集发现生成的规则
标签:growth 通过 不同的 parent str 抽取 http png +=
原文地址:https://www.cnblogs.com/lincz/p/12822261.html