标签:输出 修改 oss 创新 idea war 图像 设定 分析
期刊:IEEE SIGNAL PROCESSING LETTERS
作者:Weixuan Tang, Shunquan Tan, Bin Li, Jiwu Huang
Notes:早期将GAN用于steganography的众多算法中,个人认为这篇2017年的论文是把steganography的逻辑在GAN框架中实现的最精致的。为什么说精致,因为论文中整个算法逻辑很清晰、有一定的创新点、结构紧凑。相比于其他早期利用GAN做steganography的论文中利用GAN生成图像后做steganography,这篇论文首次利用GAN的对抗理论来学习出隐写失真,算是将GAN的理论剥离出来再应用在steganography中的首次突破。由于基于深度学习的隐写分析的发展,Xu-Net、Ye-Net、SRNet等基于深度学习的隐写分析算法纷纷出现,这也就为设计基于GAN的隐写算法提供了现成的优质组件,因此这篇文章GAN中的判别器直接用了Xu-Net。
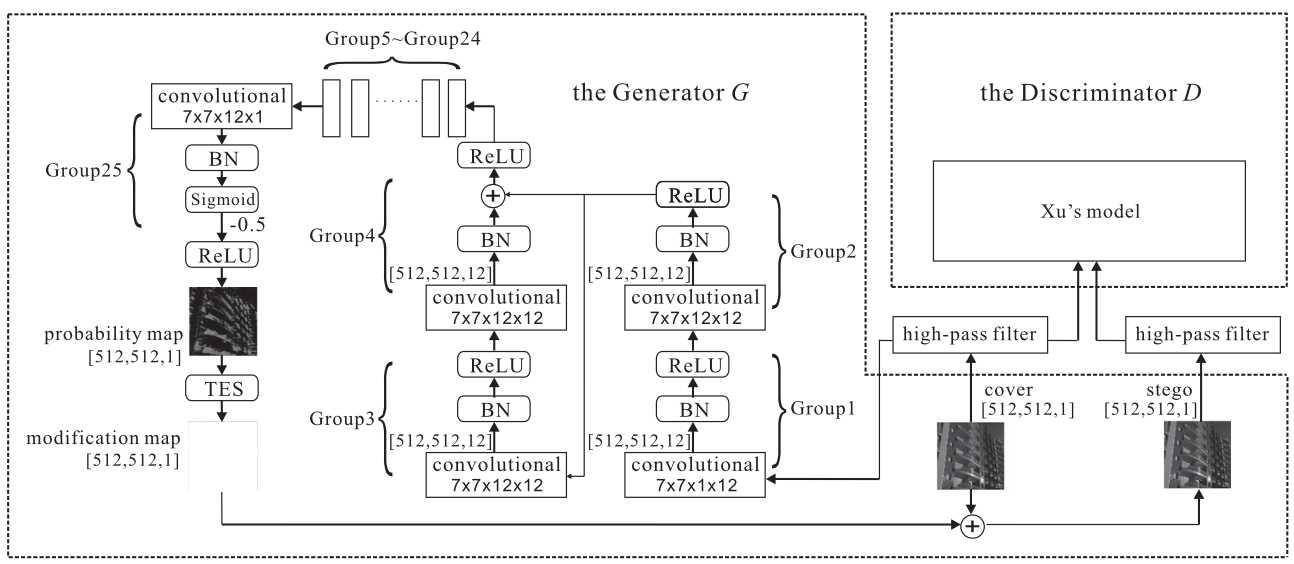
原文提出了自动隐写失真学习框架(automatic steganographic distortion learning framework with GAN, ASDL-GAN),利用GAN的对抗理论,在训练中学习判别器中隐写分析算法的隐式特征,反馈给生成器用来生成失真概率图。因此,原文也表示ASDL-GAN是在模拟加性失真的隐写算法(steganography with additive distortion)和基于深度学习的隐写分析之间的对抗过程。个人认为“模拟”应该是这篇论文的核心思想。
原文采用了PL(payload limited)的模式,即在限定一定的嵌入信息负载的同时,最小化隐写失真。在常规的隐写算法中,首先通常需要定义一个加性失真函数:
\(D(\mathtt{X},\mathtt{Y})= \sum^{H}_{i=1} \sum^{W}_{j=1} \rho_{i,j}|x_{i,j}-y_{i,j}|\)
其中\(\mathtt{X}=(x_{i,j})^{H×W}\) 和\(\mathtt{Y}=(y_{i,j})^{H×W}\) 分别代表原始载体cover和含密载体stego。\(\rho_{i,j}\)是将像素点从\(x_{i,j}\)修改为\(y_{i,j}\)的代价(cost)。对于像HUGO,S-UNIWARD这样的空域隐写算法来讲,分别有各自特定的代价函数:\(\varrho=(\rho_{i,j})^{H×W}\)。接下来就可以通过最小化失真函数的期望值来得到每个像素点的改写概率图\(\mathtt{P}=(p_{i,j})^{H×W}\)。有了这个概率图,就可以进一步实施隐写了。那么,为什么原文是将这个过程反过来,先得到概率图\(\mathtt{P}\),再去计算嵌入代价呢?——“We take the opposite approach, in which the change probabilities P are learnt first and then the corresponding embedding costs ρ can be conversely derived for practical steganographic coding scheme, e.g., Syndrome–Trellis codes”。
首先要从隐写分析说起,要想有效躲避隐写分析算法的检测,就要避免在隐写分析“重点关注”区域嵌入信息。那么,这个动作直接由改写概率图\(\mathtt{P}\)直接决定。换句话说,这个改写概率图\(\mathtt{P}\)的准确性直接影响了隐写分析的分析质量。回到原文的GAN框架中来,要想在GAN中实现隐写和隐写分析的对抗,那么这个改写概率图\(\mathtt{P}\)无疑是二者之间的纽带,通过GAN框架来训练出合适的生成器,最终使输出的改写概率图\(\mathtt{P}\)达到更安全的水平,就实现了利用GAN隐写的逻辑。
有了改写概率图\(\mathtt{P}\)这个关键的纽带,下一步要做的就是把生成器和这个改写概率图\(\mathtt{P}\)联系起来。既然上面说过可以从代价函数\(\varrho\)推导出改写概率图\(\mathtt{P}\),那么反过来也就可以从改写概率图\(\mathtt{P}\)反推出代价函数\(\varrho\),这一点在逻辑上也是成立的。在进一步,可以在GAN中通过设计Loss函数来代表代价函数\(\varrho\),这样,也就解释了原文的这个巧妙设计。
那么问题又来了,怎么才能在GAN的框架中定义Loss函数来代表代价函数\(\varrho\)呢?
很简单,由于有现成的CNN-based隐写分析框架Xu-Net作为判别器,那么判别器的Loss也就自然可以作为代价函数\(\varrho\)了。因此,就得到了生成器的第一个Loss函数:\(l_G^1=-l_D\)。那么,现在最小化失真的思路打通了,接下来就是模拟一定负载率嵌入的过程了。
这里原文采用了三段嵌入模式(ternary embedding scheme),即嵌入单位为\(\phi ∈ \{+1, ?1, 0\}\),则将\(x_{i,j}\)修改为\(x_{i,j}+\phi\)的概率定义为\(p_{i,j}^\phi\)。根据最大熵原则,\(p^{+1}_{i,j} =p^{-1}_{i,j} =p_{i,j}/2\),\(p^{0}_{i,j} =1-p_{i,j}\)。则隐写负载(原文叫做capacity,实际上为信息熵)可以得出:
\(\mathtt{capacity}=\displaystyle \sum^{H}_{i=1}\displaystyle \sum^{W}_{j=1}( -p^{+1}_{i,j} \log_2 p^{+1}_{i,j} - p^{-1}_{i,j} \log_2 p^{-1}_{i,j} - p^{0}_{i,j} \log_2 p^{0}_{i,j})\)
这个capacity作为生成器的限制条件,体现了隐写的负载。从而也就得到了生成器的另一个Loss函数:\(l_G^2=(\mathtt{capacity}?H×W×q)^2\)。
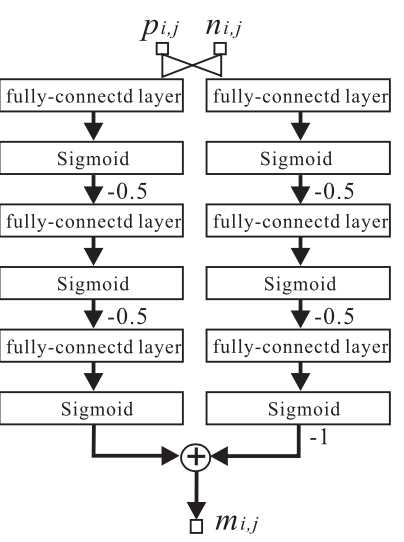
现在仿佛一切都可以就绪了,可以用GAN来训练了,但是还有很重要的一点,给隐写分析器(判别器)输送的输入应该是cover和stego,目前这个流程下来还只能得到隐写概率图P,接下来就是要设计模拟嵌入的模块来从之前得到的隐写概率图P进一步生成嵌入修改图(modification map),用来加在cover上,得到stego。实际上,这个过程可以由一个简单的三段分段函数来实现:
\(m_{i,j}‘ =\begin{cases} -1, &\text{if } {n_{i,j}<p_{i,j}/2} \\ 1, & \text{if } {n_{i,j}>1-p_{i,j}/2} \\ 0, & \text{otherwise } \end{cases}\)
但是问题又来了,如果直接将模拟嵌入的分段函数放进神经网络中,由于该函数不连续,那么就无法实现反向传播了。所以原文设计了一个简单的全连接网络TES,将TES预训练好用来模拟\(m_{i,j}‘\)。至此,也就完整实现了ASDL-GAN的完整过程。
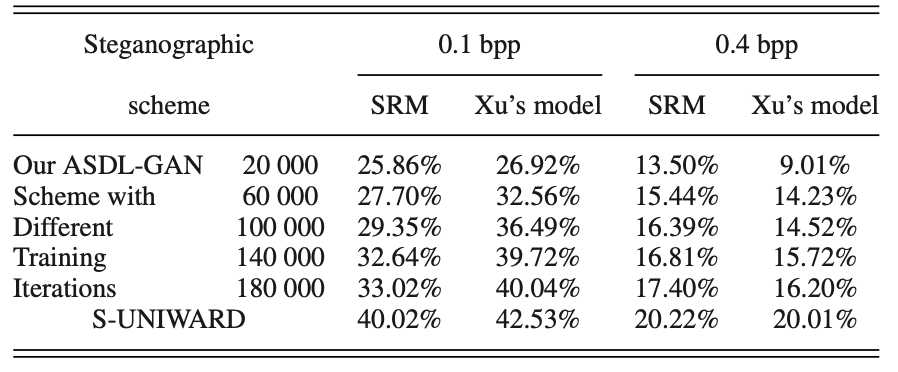
实验部分ASDL-GAN的主要对比对象是S-UNIWARD算法。可能由于TES、损失函数的设计以及具体网络参数设定的问题,ASDL-GAN的实验效果并没有非常理想。-“However, we have to acknowledge that even with large training iterations, ASDL-GAN is still inferior to state-of-the- art hand-crafted steganographic algorithms, e.g., S-UNIWARD, which may attribute to the lack of training samples. As a large-scale deep-learning framework, ASDL-GAN is hindered by insufficient 40 000 training samples.” 但是,不得不说ASDL-GAN确实是一个不错的idea。
信息隐藏系列-1:Automatic Steganographic Distortion Learning Using a Generative Adversarial Network
标签:输出 修改 oss 创新 idea war 图像 设定 分析
原文地址:https://www.cnblogs.com/keyky/p/12823074.html