标签:numpy max lse color gauss 技术 lang cal 数值
详细实验指导见上一篇,此处只写内容啦
实验内容: 求解如下4元线性方程组的近似解。
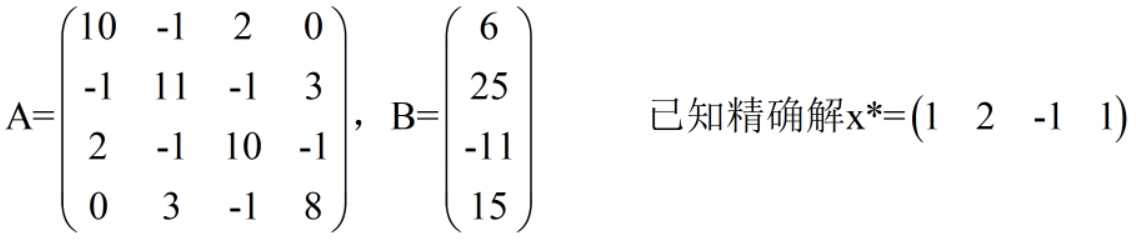
• Jacobi迭代过程
1 import numpy as np 2 3 A = np.array([[10,-1,2,0],[-1,11,-1,3],[2,-1,10,-1],[0,3,-1,8]]) 4 B = np.array([6, 25, -11, 15]) 5 x0 = np.array([0.0, 0, 0, 0]) 6 x = np.array([0.0, 0, 0, 0]) 7 8 times = 0 9 10 while True: 11 for i in range(4): 12 temp = 0 13 for j in range(4): 14 if i != j: 15 temp += x0[j] * A[i][j] 16 x[i] = (B[i] - temp) / A[i][i] 17 calTemp = max(abs(x - x0)) 18 times += 1 19 if calTemp < 1e-5: 20 break 21 else: 22 x0 = x.copy() 23 24 print(times) 25 print(x)
运行结果:

•Gauss-Seidel迭代
1 import numpy as np 2 3 A = np.array([[10,-1,2,0],[-1,11,-1,3],[2,-1,10,-1],[0,3,-1,8]]) 4 B = np.array([6, 25, -11, 15]) 5 x0 = np.array([0.0, 0, 0, 0]) 6 x = np.array([1.0, 2, -1, 1]) 7 times = 0 8 9 while True: 10 for i in range(4): 11 temp = 0 12 tempx = x0.copy() 13 for j in range(4): 14 if i != j: 15 temp += x0[j] * A[i][j] 16 x[i] = (B[i] - temp) / A[i][i] 17 x0[i] = x[i].copy() 18 calTemp = max(abs(x - tempx)) 19 times += 1 20 if calTemp < 1e-5: 21 break 22 else: 23 x0 = x.copy() 24 25 print(times) 26 print(x)
运行结果:

• SOR迭代法
1 import numpy as np 2 3 A = np.array([[10,-1,2,0],[-1,11,-1,3],[2,-1,10,-1],[0,3,-1,8]]) 4 B = np.array([6, 25, -11, 15]) 5 x0 = np.array([0.0, 0, 0, 0]) 6 x = np.array([1.0, 2, -1, 1]) 7 w = 1.2 8 times, MT = 0, 1000 9 10 while times < MT: 11 tempx = x0.copy() 12 for i in range(4): 13 temp = 0 14 for j in range(4): 15 if i != j: 16 temp += x0[j] * A[i][j] 17 x[i] = (B[i] - temp) / A[i][i] 18 x0[i] = x[i] 19 x = w * x + (1-w) * tempx 20 calTemp = max(abs(x - tempx)) 21 times += 1 22 if calTemp < 1e-5: 23 break 24 print(times) 25 print(x)
运行结果:
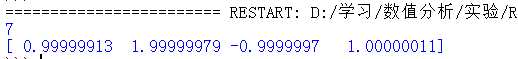
标签:numpy max lse color gauss 技术 lang cal 数值
原文地址:https://www.cnblogs.com/ynly/p/12828100.html