标签:取出 i++ 问题 序列 while scanf delete 第一个 zju
注:本文使用的网课资源为中国大学MOOC
https://www.icourse163.org/course/ZJU-93001
void X_Sort( ElementType A[], int N )
基本思想:
时间复杂度:
稳定性:是
void Bubble_Sort( ElementType A[], int N )
{
int P,i,flag;
for (P=N-1; P>=0; P--)
{
flag = 0;
for (i=0; i<P; i++)
{
// 一趟冒泡
if (A[i] > A[i+1])
{
Swap(A[i], A[i+1]);
flag = 0; // 标识发生了交换
}
}
if (flag==0) // 如果第一趟冒泡全程无交换
break;
}
}
基本思想:
时间复杂度:
稳定性:是
void Insertion_Sort( ElementType A[], int N )
{
int P, i;
ElementType Tmp;
for ( P=1; P<N; P++ )
{
Tmp = A[P]; // 取出未排序序列中的第一个元素
for ( i=P; i>0 && A[i-1]>Tmp; i-- )
A[i] = A[i-1]; // 依次与已排序序列中元素比较并右移
A[i] = Tmp; // 放进合适的位置
}
}
——(34,8) (34,32) (34,21) (64,51) (64,32) (64,21) (51,32) (51,21) (32,21)
——如果序列基本有序,则插入排序简单且高效
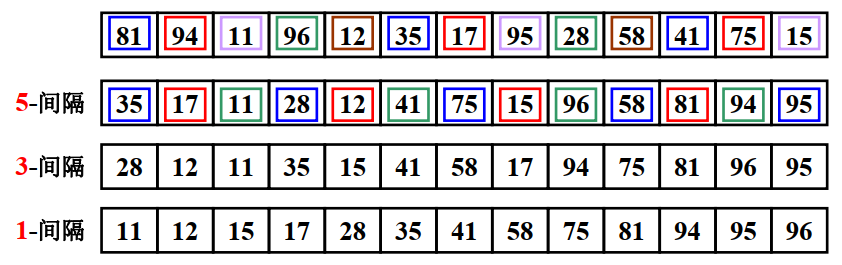
归纳为:
原始希尔排序 : \(D_M = \left \lfloor N/2 \right \rfloor, D_k = \left \lfloor D_{k+1}/2 \right \rfloor\)
void Shell_Sort( ElementType A[], int N )
{
int D,P,i;
ElementType Tmp;
for ( D=N/2; D>0; D/=2 ) // 希尔增量序列
{
for ( P=D; P<N; P++) // 插入排序
{
Tmp = A[P];
for ( i=P; i>=D && A[i-D]>Tmp; i-=D )
A[i] = A[i-D];
A[i] = Tmp;
}
}
}
Hibbard增量序列
Sedgewick增量序列
/* 希尔排序 - 用Sedgewick增量序列 */
void ShellSort( ElementType A[], int N )
{
int Si, D, P, i;
ElementType Tmp;
/* 这里只列出一小部分增量 */
int Sedgewick[] = {929, 505, 209, 109, 41, 19, 5, 1, 0};
for ( Si=0; Sedgewick[Si]>=N; Si++ )
; /* 初始的增量Sedgewick[Si]不能超过待排序列长度 */
for ( D=Sedgewick[Si]; D>0; D=Sedgewick[++Si] )
for ( P=D; P<N; P++ ) /* 插入排序*/
{
Tmp = A[P];
for ( i=P; i>=D && A[i-D]>Tmp; i-=D )
A[i] = A[i-D];
A[i] = Tmp;
}
}
思路:
void Selection_Sort( ElementType A[], int N )
{
int i, MinPosition;
for ( i=0; i<N; i++ )
{
// 从A[i]到A[N–1]中找最小元,并将其位置赋给MinPosition
MinPosition = ScanForMin( A, i, N-1 );
// 将未排序部分的最小元换到有序部分的最后位置
Swap( A[i], A[MinPosition])
}
}
思路:与选择排序类似,但是改变最小元的扫描策略,利用堆结构扫描
算法1
思路:
因此:
void Heap_Sort( ElementType A[], int N )
{
BuildHeap(A); // 将数组A调整为堆,复杂度为O(N)
for ( i=0; i<N; i++ )
TmpA[i] = DeleteMin(A); // 依次弹出根结点,此时 O(logN)
for ( i=0; i<N; i++ )
A[i] = TmpA[i]; // 直接赋值,此时复杂度为O(N)
}
算法2:
思路:
/* 交换 */
void Swap( ElementType *a, ElementType *b )
{
ElementType t = *a; *a = *b; *b = t;
}
/* 将N个元素的数组中以A[p]为根的子堆调整为最大堆 */
void PercDown( ElementType A[], int p, int N )
{
int Parent, Child;
ElementType X;
X = A[p]; /* 取出根结点存放的值 */
for( Parent=p; (Parent*2+1)<N; Parent=Child )
{
Child = Parent * 2 + 1;
if( (Child!=N-1) && (A[Child]<A[Child+1]) )
Child++; /* Child指向左右子结点的较大者 */
if( X >= A[Child] )
break; /* 找到了合适位置 */
else /* 下滤X */
A[Parent] = A[Child];
}
A[Parent] = X;
}
/* 堆排序 */
void HeapSort( ElementType A[], int N )
{
int i;
for ( i=N/2-1; i>=0; i-- )/* 建立最大堆 */
PercDown( A, i, N );
for ( i=N-1; i>0; i-- )
{
/* 删除最大堆顶 */
Swap( &A[0], &A[i] );
PercDown( A, 0, i );
}
}
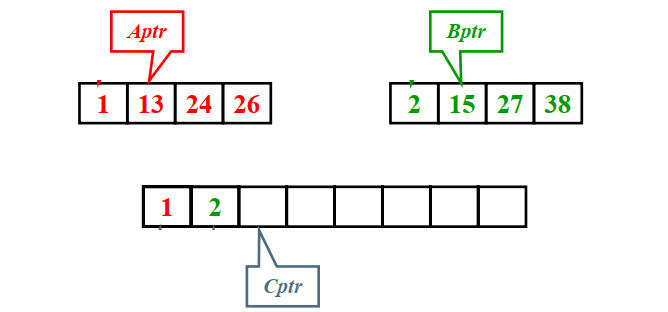
将子序列A,B的元素依次比较,合并成C序列
/* L = 左边起始位置, R = 右边起始位置, RightEnd = 右边终点位置 */
void Merge( ElementType A[], ElementType TmpA[], int L, int R, int RightEnd )
{
int LeftEnd, Tmp, NumElements;
LeftEnd = R - 1; // 左边终点位置。假设左右两列挨着
Tmp = L; // 存放结果的数组的初始位置
NumElements = RightEnd - L + 1;
while ( L<=LeftEnd && R<=RightEnd )
{
if ( A[L] <= A[R] )
TmpA[Tmp++] = A[L++];
else
TmpA[Tmp++] = A[R++];
}
while( L <= LeftEnd ) // 直接复制左边剩下的
TmpA[Tmp++] = A[L++];
while( R <= RightEnd ) // 直接复制右边剩下的
TmpA[Tmp++] = A[R++];
for( i = 0; i < NumElements; i++, RightEnd -- )
A[RightEnd] = TmpA[RightEnd];
}
void MSort( ElementType A[], ElementType TmpA[], int L, int RightEnd )
{
int Center;
if ( L < RightEnd )
{
Center = ( L + RightEnd ) / 2;
MSort( A, TmpA, L, Center );
MSort( A, TmpA, Center+1, RightEnd );
Merge( A, TmpA, L, Center+1, RightEnd );
}
}
可以推得:T(N) = T(N/2)+T(N/2)+O(N) --> T(N)=O(N logN )
统一函数接口
void Merge_sort( ElementType A[], int N )
{
ElementType *TmpA;
TmpA = (ElementType *)malloc(N*sizeof( ElementType ))
if ( TmpA != NULL )
{
MSort(A, TmpS, 0, N-1);
free( TmpA );
}
else
Error("空间不足");
}
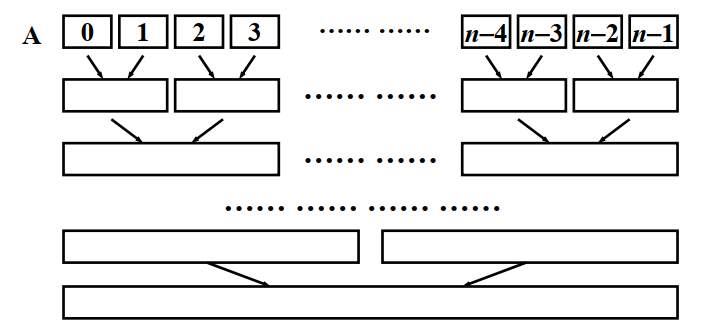
思路:
/* 归并排序 - 循环实现 */
/* 两两归并相邻有序子列 */
/* length = 当前有序子列的长度*/
void Merge_pass( ElementType A[], ElementType TmpA[], int N, int length )
{
int i, j;
for ( i=0; i <= N-2*length; i += 2*length ) // 首先只考虑偶数子列的情况
Merge( A, TmpA, i, i+length, i+2*length-1 ); // 与递归版本中的Merge函数一致
if ( i+length < N ) /* 归并最后2个子列*/
Merge( A, TmpA, i, i+length, N-1);
else /* 最后只剩1个子列*/
{
for ( j = i; j < N; j++ )
TmpA[j] = A[j];
}
}
void Merge_Sort( ElementType A[], int N )
{
int length;
ElementType *TmpA;
length = 1; /* 初始化子序列长度*/
TmpA = malloc( N * sizeof( ElementType ) );
if ( TmpA != NULL )
{
while( length < N )
{
Merge_pass( A, TmpA, N, length );
length *= 2;
Merge_pass( TmpA, A, N, length ); // 保证最后的排序结果存储在数组A中
length *= 2;
}
free( TmpA );
}
else
printf( "空间不足" );
}
结论:
标签:取出 i++ 问题 序列 while scanf delete 第一个 zju
原文地址:https://www.cnblogs.com/Superorange/p/12831402.html