标签:arp div har 思路 root 开始 需要 个数 trie
维护一个字符串集合,支持两种操作: “I x”向集合中插入一个字符串x; “Q x”询问一个字符串在集合中出现了多少次。 共有N个操作,输入的字符串总长度不超过 105,字符串仅包含小写英文字母。 输入格式 第一行包含整数N,表示操作数。 接下来N行,每行包含一个操作指令,指令为”I x”或”Q x”中的一种。 输出格式 对于每个询问指令”Q x”,都要输出一个整数作为结果,表示x在集合中出现的次数。 每个结果占一行。 数据范围 1≤N≤2∗104 输入样例: 5 I abc Q abc Q ab I ab Q ab 输出样例: 1 0 1
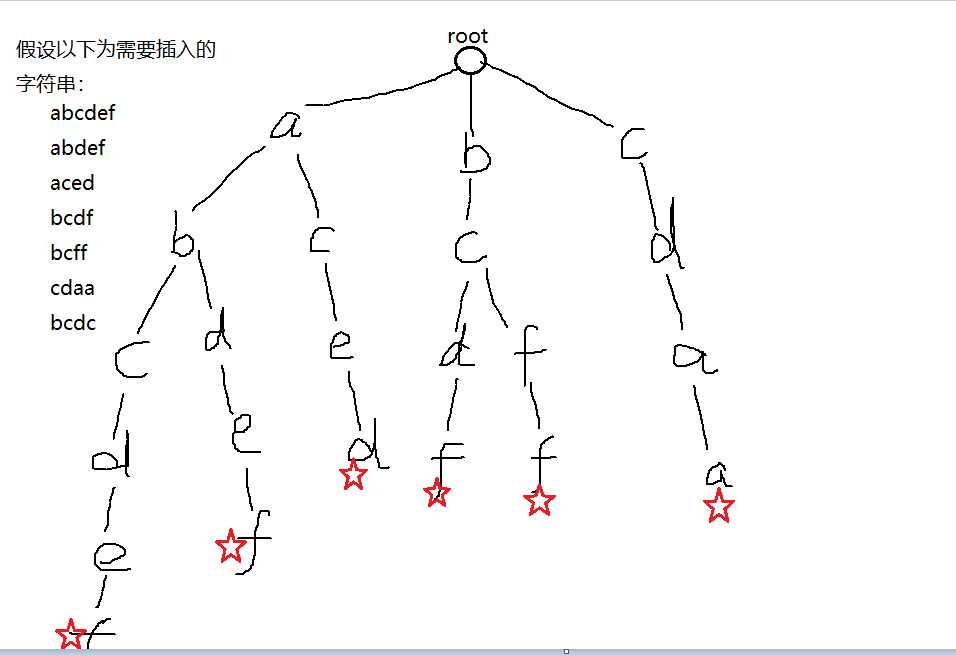
此处主要为插入和查询功能,可以画成一棵树来理解(不一定是二叉树)。
插入功能:树从根节点开始往下走,如下图中需要插入abcdef时,如果本身树中没有这个字符串,
就一直往下更新结点,直到更新完一个完整的串后需要标上红色星星。标上红星的原因是为了记录当前字符串是否每个字母都已经插入完毕,如果没有标记,那么
当我插入完abcdef以后再插入一个abc,那么查询的时候就没办法被发现了。
查询功能:返回树中该字符串红星个数,如果没有这个串就返回-1。
如图
#include <iostream>
using namespace std;
const int N = 100010;
int ctn[N], son[N][26], idx; //ctn代表以当前结点结尾的字符串个数;son二维数组表示每个结点中又有可能延申26个子结点;idx表示结点下标
char str[N]; //存储字符串
void insert(char *str){
int p = 0;
for(int i = 0; str[i]; i++){
int u = str[i] - ‘a‘; //把字符串中的每一个字母转换成数字
if(!son[p][u]) son[p][u] = ++ idx; //从root开始遍历,如果当前树中没有这个字符结点,那就让创造一个新的结点来存储,即新增idx
p = son[p][u]; //每存储一个字符更新一下结点树
}
ctn[p] ++ ; //插入完毕以后ctn增加该字符串的出现次数
}
int query(char *str){ //查询与插入大体相同
int p = 0;
for(int i = 0; str[i]; i++){
int u = str[i] - ‘a‘;
if(!son[p][u]) return 0; //如果当前树中并没有该字符串直接返回0
p = son[p][u];
}
return ctn[p]; //查询结果返回字符串出现次数
}
int main(){
int n;
scanf("%d", &n);
while(n --){
char op[2];
scanf("%s%s", op, str);
if(*op == ‘I‘) insert(str);
else printf("%d\n", query(str));
}
return 0;
}
如果有不完整的地方待补充。
标签:arp div har 思路 root 开始 需要 个数 trie
原文地址:https://www.cnblogs.com/LinawZ/p/12831412.html