标签:mamicode mit 原理 NPU height float limit 浮点 平均数
博主是高中生,前几天学到了初级的线性回归方程。总用卡西欧敲然后带入公式实在有些麻烦。于是心血来潮用Python实现了一下~
原理:求线性回归方程:

求决定系数:
代码:
# -*- coding:UTF-8 -*- import numpy as np #输入开始 li = list(input("输入xi:").split()) lis = list(input("输入yi: ").split()) lenth = len(li)#项数 def getlist(listname): ul=[] for a in listname: ul.append(float(a)) return(ul) #输入结束 #转float开始 ul_xi=getlist(li) ul_yi=getlist(lis) #转float结束 xiaver=np.mean(ul_xi)#求xi平均数 yiaver=np.mean(ul_yi)#求yi平均数 #求xiyi开始 func = lambda x,y: x*y result_xiyi = map(func,ul_xi,ul_yi) xiyi_list = list(result_xiyi) ul_xiyi = getlist(xiyi_list) xiyi_aver = np.mean(ul_xiyi) xiyi = xiyi_aver*lenth #求xiyi结束 #求xi2开始 result_xi2 = map(func,ul_xi,ul_xi) xi2_list = list(result_xi2) ul_xi2 = getlist(xi2_list) xi2_aver = np.mean(ul_xi2) xi2=xi2_aver*lenth #求xi2结束 #带入公式开始 b=(xiyi - lenth * xiaver * yiaver) / (xi2 - lenth * xiaver*xiaver ) a= yiaver - b * xiaver #带入公式结束 #计算残差开始 def eicalc(x): return(x *b +a) li_aftr_calc=list(map(eicalc,ul_xi)) func_ei = lambda x,y: x-y result_ei = list(map(func_ei,ul_yi,li_aftr_calc))#残差所得 #计算残差结束 #计算决定系数开始 #计算残差平方和 def r2calc(x): return(x**2) li_eisquare = list(map(r2calc,result_ei)) eisquare_aver = np.mean(li_eisquare) eisquare = eisquare_aver * lenth #计算总偏差平方和 def pianchacalc(x): return((x - yiaver)**2) li_piancha = list(map(pianchacalc,ul_yi)) piancha_aver = np.mean(li_piancha) piancha = piancha_aver * lenth #带入公式 R2 = 1 - (eisquare / piancha) #计算决定系数结束 #输出 print("线性回归方程为: y="+str(b)+"x+"+str(a)) print("残差列表为:") print(result_ei) print("决定系数R2为:"+str(R2))
输出:
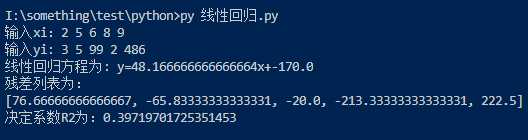
注意事项:
标签:mamicode mit 原理 NPU height float limit 浮点 平均数
原文地址:https://www.cnblogs.com/coder106/p/12859704.html