标签:实现 目标 类型 cross tar pre dict aci 手工
1.理解分类与监督学习、聚类与无监督学习。
简述分类与聚类的联系与区别。
简述什么是监督学习与无监督学习。
答:
(1)分类和聚类:
联系:
分类和聚类都是把每一条记录归应到相应的类别里,都包含这一过程,对于想要 分析的目标点,都会在数据集中寻找离它最近的点,二者都用到了NN算法。
区别:
1)分类的目的是为了确定一个点的类别,类别是已知的 ,聚类的目的是将一系列点分成若干类,类别是未知的;
2)分类是一种监督学习如kNN算法,聚类是一种无监督学习如K-Means算法;
(2)
监督学习:
利用已标记的训练数据集(X,Y),通过训练数据集学习建立一个成模型,实现对新数据的分类预测。每个实例都是由一个输入对象(通常为矢量)和一个期望的输出值(也称为监督信号)组成,任务是分类和回归。
无监督学习:
无监督学习是在缺乏先验知识的情况下(只输入X,没有Y)利用一些未经过标记的数据来发现其中隐藏的一些规律并做出相应,任务是聚类和降维。
2.朴素贝叶斯分类算法 实例
利用关于心脏病患者的临床历史数据集,建立朴素贝叶斯心脏病分类模型。
有六个分类变量(分类因子):性别,年龄、KILLP评分、饮酒、吸烟、住院天数
目标分类变量疾病:
–心梗
–不稳定性心绞痛
新的实例:–(性别=‘男’,年龄<70, KILLP=‘I‘,饮酒=‘是’,吸烟≈‘是”,住院天数<7)
最可能是哪个疾病?
上传手工演算过程。
|
|
性别 |
年龄 |
KILLP |
饮酒 |
吸烟 |
住院天数 |
疾病 |
|
1 |
男 |
>80 |
1 |
是 |
是 |
7-14 |
心梗 |
|
2 |
女 |
70-80 |
2 |
否 |
是 |
<7 |
心梗 |
|
3 |
女 |
70-81 |
1 |
否 |
否 |
<7 |
不稳定性心绞痛 |
|
4 |
女 |
<70 |
1 |
否 |
是 |
>14 |
心梗 |
|
5 |
男 |
70-80 |
2 |
是 |
是 |
7-14 |
心梗 |
|
6 |
女 |
>80 |
2 |
否 |
否 |
7-14 |
心梗 |
|
7 |
男 |
70-80 |
1 |
否 |
否 |
7-14 |
心梗 |
|
8 |
女 |
70-80 |
2 |
否 |
否 |
7-14 |
心梗 |
|
9 |
女 |
70-80 |
1 |
否 |
否 |
<7 |
心梗 |
|
10 |
男 |
<70 |
1 |
否 |
否 |
7-14 |
心梗 |
|
11 |
女 |
>80 |
3 |
否 |
是 |
<7 |
心梗 |
|
12 |
女 |
70-80 |
1 |
否 |
是 |
7-14 |
心梗 |
|
13 |
女 |
>80 |
3 |
否 |
是 |
7-14 |
不稳定性心绞痛 |
|
14 |
男 |
70-80 |
3 |
是 |
是 |
>14 |
不稳定性心绞痛 |
|
15 |
女 |
<70 |
3 |
否 |
否 |
<7 |
心梗 |
|
16 |
男 |
70-80 |
1 |
否 |
否 |
>14 |
心梗 |
|
17 |
男 |
<70 |
1 |
是 |
是 |
7-14 |
心梗 |
|
18 |
女 |
70-80 |
1 |
否 |
否 |
>14 |
心梗 |
|
19 |
男 |
70-80 |
2 |
否 |
否 |
7-14 |
心梗 |
|
20 |
女 |
<70 |
3 |
否 |
否 |
<7 |
不稳定性心绞痛 |


3.使用朴素贝叶斯模型对iris数据集进行花分类。
尝试使用3种不同类型的朴素贝叶斯:
并使用sklearn.model_selection.cross_val_score(),对各模型进行交叉验证。
from sklearn.datasets import load_iris #引入sklean的高斯贝叶斯,多项式型贝叶斯,伯努利型贝叶斯 from sklearn.naive_bayes import GaussianNB, MultinomialNB, BernoulliNB #引入sklean的交叉验证分数 from sklearn.model_selection import cross_val_score # 鸢尾花数据集 iris = load_iris() # 鸢尾花花瓣长度数据 data = iris[‘data‘] # 分类结果 target = iris[‘target‘] # 高斯分布型 gnb_model = GaussianNB() # 构建高斯分布模型 gnb_model.fit(data, target) # 训练模型 gnb_pre = gnb_model.predict(data) # 预测模型 print("高斯贝叶斯的预测结果",gnb_pre) gnb_result=sum(gnb_pre == target) / len(data) print("高斯分布模型准确率为:%.3F" %gnb_result ) # 进行交叉验证 # cross_val_score(训练数据,测试数据,验证次数) gnb_score = cross_val_score(gnb_model, data, target, cv=10) print(‘经过十轮交叉验证过的高斯分布模型的精确率:%.3F‘ % gnb_score.mean()) # 多项式型贝叶斯 mnb_model = MultinomialNB() # 构建多项式模型 mnb_model.fit(data, target) # 训练模型 mnb_pre = mnb_model.predict(data) # 预测模型 print("多项式型贝叶斯的预测结果",mnb_pre) mnb_result=sum(mnb_pre == target) / len(data) print("多项式模型准确率为:%.3F" % mnb_result) mnb_score = cross_val_score(mnb_model, data, target, cv=10) print(‘经过十轮交叉验证过的多项式贝叶斯模型的精确率:%.3F‘ % mnb_score.mean()) # 伯努利型 bnb_model = BernoulliNB() # 构建伯努利模型 bnb_model.fit(data, target) # 训练模型 bnb_pre = bnb_model.predict(data) # 预测模型 print("伯努利贝叶斯的预测结果",bnb_pre) bnb_result=sum(bnb_pre == target) / len(data) print("伯努利贝叶斯模型准确率为:%.3F" % bnb_result) bnb_score = cross_val_score(bnb_model, data, target, cv=10) print(‘经过十轮交叉验证过的伯努利贝叶斯模型的精确率:%.3F‘ % bnb_score.mean())
结果如下所示
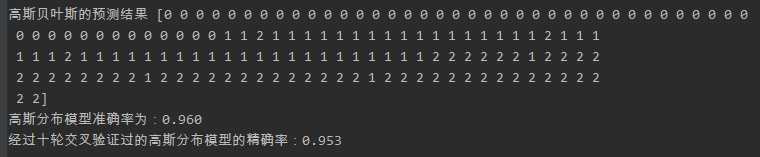
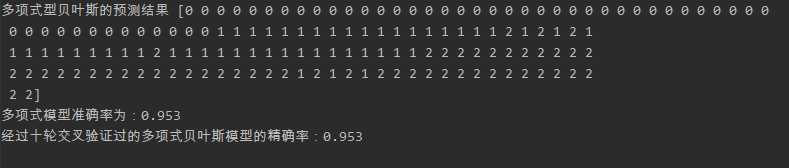

由此可见高斯贝叶斯模型以及多项式贝叶斯模型对于预测鸢尾花数据较为适合
标签:实现 目标 类型 cross tar pre dict aci 手工
原文地址:https://www.cnblogs.com/chock/p/12870625.html