标签:表示 struct nbsp 记录 body 取出 集合 create 创建
最近翻看之前写的一些东西,看到了这个。
首先我们先来分析一下
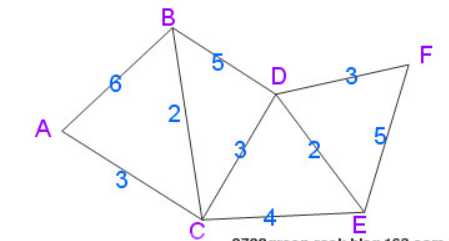
其基本思想是,设置顶点集合S并不断地作贪心选择来扩充这个集合。一个顶点属于集合S当且仅当从源到该顶点的最短路径长度已知。初始时,S中仅含有源。设u是G的某一个顶点,把从源到u且中间只经过S中顶点的路称为从源到u的特殊路径,并用数组dist记录当前每个顶点所对应的最短特殊路径长度。Dijkstra算法每次从V-S中取出具有最短特殊路长度的顶点u,将u添加到S中,同时对数组dist作必要的修改。一旦S包含了所有V中顶点,dist就记录了从源到所有其它顶点之间的最短路径长度。
|
迭代 |
S |
u |
D[2] |
D[3] |
D[4] |
D[5] |
D[6] |
|
初始 |
{1} |
NULL |
6 |
3 |
∞ |
∞ |
∞ |
|
1 |
{1,3} |
3 |
5 |
3 |
6 |
7 |
∞ |
|
2 |
{1,3,2} |
2 |
5 |
3 |
6 |
7 |
∞ |
|
3 |
{1,3,2,4} |
4 |
5 |
3 |
6 |
7 |
9 |
|
4 |
{1,3,2,45} |
5 |
5 |
3 |
6 |
7 |
9 |
|
5 |
{1,3,2,45,6} |
6 |
5 |
3 |
6 |
7 |
9 |
由表格的最后一行可以得知1点到达个点的最近距离。
首先来个简单的,不使用结构体,直接定义。
#include<stdio.h> #define maxnum 100 #define maxint 65535 int dist[maxnum]; //最短路径 int prev[maxnum]; //当前节点前一个节点 int arc[maxnum][maxnum]; void Dijkstra(int n, int t, int v, int* dist, int* prev, int arc[maxnum][maxnum]) { bool s[maxnum]; for (int i = 1; i <= n; ++i) //将有权值的边prev=前一个点 无权值的边prev=0 { dist[i] = arc[v][i]; s[i] = 0; if (dist[i] == maxint) prev[i] = 0; else prev[i] = v; } dist[v] = 0; s[v] = 1; //v是起点放在s[]中 for(int i=1;i<=n;++i) { int u = v; int tmp = maxint; //找出距离v点最近的点 放入到s中 for(int j=1;j<=n;++j) { if (!s[j] && dist[j] < tmp) { u = j; tmp = dist[j]; } } s[u] = 1; //将最近的点放在s中 for (int j = 1; j <= n; ++j) { if (!s[j] && arc[u][j] < maxint) { int newdist = dist[u] + arc[u][j]; if (newdist < dist[j]) { dist[j] = newdist; prev[j] = u; } } } } } void searchPath(int* prev, int v, int u) { int que[maxnum]; int tot = 1; que[tot] = u; tot++; int tmp = prev[u]; while (tmp != v) { que[tot] = tmp; tot++; tmp = prev[tmp]; } que[tot] = v; for (int i = tot; i >= 1; --i) { if (i != 1) printf("%d->", que[i]); else printf("%d\n", que[i]); } } int main() { int n ,link; //n为点数,link为边数; scanf_s("%d\n%d\n", &n,&link); int p, q, len; //p、q表示有边的两个点,len表示边的权值; for (int i = 1; i <= n; ++i) for (int j = 1; j <= n; ++j) arc[i][j] = maxint; for (int i = 1; i <= link; ++i) { scanf_s("%d %d %d", &p, &q, &len); if (len < arc[p][q]) { arc[p][q] = len; arc[q][p]=len; //有这个为无向图 } }for (int i = 1; i <= n; ++i) { for (int j = 1; j <= n; ++j) printf("%d ", arc[i][j]); printf("\n"); } printf("请输入起点和终点:\n"); int a, b; scanf_s("%d %d", &a, &b); getchar(); printf("%d到%d的最短距离为:", a, b); Dijkstra(n,b, a, dist, prev, arc); printf("%d\n", dist[b]); printf("%d到%d的最短路径为:",a,b); searchPath(prev, a, b); return 0; }
上边的比较简单粗暴。
学了这么长时间的C语言怎么能没有一点长进。
基础的一些定义及结构体
#define maxnum 100 //存放最大点数 #define int_max 65535 //存放正无穷 int dist[maxnum]; //最短距离 int prev[maxnum]; //前驱节点 typedef struct{ char vexs[maxnum]; //存放节点 int vexsum; //存放节点数 int edgsum; //存放边数 int arc[maxnum][maxnum]; //邻接矩阵 }graph; void Dijkstra(graph *G,int v0); //最短距离算法 void searchPath(int v0,int i); //最短路径算法 void creategraph(graph *G);
创建图方法void creategraph(graph* G)
{ printf("%p\n", &dist); printf("%p\n", &G->arc); char v1, v2; int len; int x, y; x = y = 0; printf("请输入有向图的节点数及边数:"); scanf_s("%d %d", &G->vexsum, &G->edgsum); getchar(); printf("请输入节点的值:"); //fflush(stdin); for (int i = 1; i <= G->vexsum; ++i) { scanf_s("%c", &G->vexs[i],sizeof(G->vexs[i])); getchar(); } for(int i=1;i<=G->vexsum;++i) //初始化邻接矩阵 for (int j = 1; j <= G->vexsum; ++j) { G->arc[i][j]=int_max; } for (int i = 1; i <= G->edgsum; ++i) { //fflush(stdin); printf("请输入边的顶点及权值:"); scanf_s("%c %c %d", &v1,1, &v2,1, &len); getchar(); for (int j = 1; j <= G->vexsum; ++j) { //用字符查找对应的位置 if (v1 == G->vexs[j]) x = j; } for (int n = 1; n <= G->vexsum; ++n) { if (v2 == G->vexs[n]) y = n; } G->arc[x][y] = len;
} }
最短距离算法
void Dijkstra(graph* G, int v0) { int s[maxnum]; for (int i = 1; i <= G->vexsum; ++i) { dist[i] = G->arc[v0][i]; s[i] = 0; if (dist[i] == int_max) prev[i] = 0; else prev[i] = v0; } s[v0] = 1; dist[v0] = 0; for (int i = 1; i <= G->vexsum; ++i) { int u = v0; int temp = int_max; for (int j = 1; j <= G->vexsum; ++j) { if (dist[j] < temp && !s[j]){ u = j; temp = dist[j]; } } s[u] = 1; for (int j = 1; j <= G->vexsum; ++j) { if (!s[j] && G->arc[u][j] < int_max) { int newdist = dist[u] +G->arc[u][j]; if (newdist < dist[j]) { dist[j] = newdist; prev[j] = u; } } } } }
最短路径算法
void searchPath(int v0, int i) { int que[maxnum]; int tot = 1; que[tot] = i; tot++; int temp = prev[i]; while (temp != v0) { que[tot] = temp; tot++; temp = prev[temp]; } que[tot] = v0; for (int i = tot; i >= 1; --i) { if (i != 1) printf("%d->", que[i]); else printf("%d\n", que[i]); } }
主函数
int main() { graph G; char dot; int v0=0; creategraph(&G); printf("请输入起始点:"); scanf_s("%c", &dot,1); getchar(); for (int j = 1; j<=G.vexsum; ++j) { if (dot == G.vexs[j]) v0 = j; } Dijkstra(&G, v0); for (int i = 1; i <= G.vexsum; ++i) { if (dist[i] < int_max) { printf("%c到%c的最短距离为:%d\n",dot,G.vexs[i],dist[i]); printf("%c到%c的最短路径为:", dot, G.vexs[i]); searchPath(v0,i); } } }
标签:表示 struct nbsp 记录 body 取出 集合 create 创建
原文地址:https://www.cnblogs.com/zhangxufei/p/12870100.html