标签:util 图片 oid rgs new style height alt http
一、实验目的
许多工程技术和数学研究中要用到定积分,如果无法直接算不出精确值(如含在积分方程中的积分)或计算困难但可用近似值近似时,就用数值积分法方法加以解决。常用的算法有:复化梯形、辛甫生(Simpson)、柯特斯(Cotes)求积法; 龙贝格(Romberg)算法;高斯(Gauss)算法。
二、实验原理

三、实验程序
下面给出复化Simpson求积法程序(梯形及柯特斯复化求积分程序可比照编制):

四、实验内容
选择 y=arctan(x) 在0-1上的积分
五、实验程序
• 复化梯形算法
1 package shuzhifenxi; 2 3 import java.util.Scanner; 4 5 public class fuhuatixing { 6 public static void main(String args[]) { 7 Scanner sc = new Scanner(System.in); 8 9 System.out.println("输入区间下限:"); 10 double a = sc.nextDouble(); 11 System.out.println("输入区间上限:"); 12 double b = sc.nextDouble(); 13 14 System.out.println("输入将区间分成的份数:"); 15 double h=sc.nextInt(); 16 17 compoundTrapezium(a,b,h); 18 } 19 20 //复化梯形公式 21 public static void compoundTrapezium(double a,double b,double h){ 22 23 double value=0; //记录最终数值 24 double contain=0; //记录一个中间值 25 for(double k=1;k<=h-1;k++){ 26 contain=contain+f(a+k*((b-a)/h)); //调用公式 27 } 28 contain=2*contain; //调用公式 29 value=((b-a)/(2*h))*(f(a)+f(b)+contain); //调用公式 30 31 System.out.println("复化梯形公式所得到结果为:"+value); 32 } 33 34 //用给定公式计算相应数值 35 public static double f(double x) { 36 37 double value=0; //记录经过公式算出来的值 38 39 value=Math.atan(x); 40 41 return value; 42 } 43 }
运行结果:
将区间分成50份所得结果:

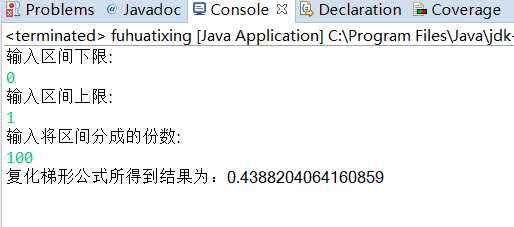
将区间分成100份所得结果:
标签:util 图片 oid rgs new style height alt http
原文地址:https://www.cnblogs.com/ynly/p/12878598.html