标签:结果 递推 amp 组合 nbsp oid for 变量 htm
动态规划01背包实现:
借鉴的这篇博文:
https://www.cnblogs.com/Christal-R/p/Dynamic_programming.html
题目:在背包容量为8的情况下,根据下图的数据动态规划得到最优解,实现右图所示的程序代码
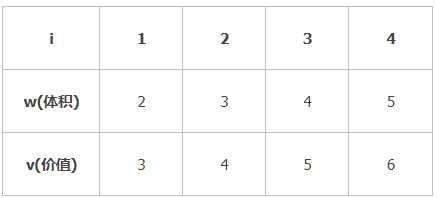
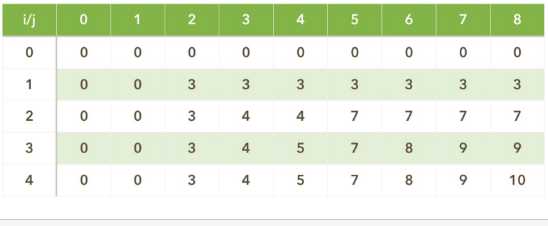
最重要的就是寻找递推关系式:
定义V[i,j]:当背包容量为j时,前i个物品最佳组合对应的值。
递推关系:
(1)当背包的容量不允许装入第i件物品时,和前一个物品装入背包一样。即 :V[i][j]=V[i-1][j]
(2)当背包的容积可以装入第i件物品时,分两种情况,A装入第i件物品不是最优,还不如不装。B装入第i件物品是最优。即:V[i][j]=max(V[i-1][j],V[i][j-w[i]]+v[i])
代码实现:
#include<iostream>
using namespace std;
int w[5]={0,2,3,4,5};
int v[5]={0,3,4,5,6};
int V[5][9];
int c=8;
int B()
{
int i,j;
for(i=0;i<5;i++)
{
V[i][0]=0;
for(j=0;j<c+1;j++)
{
V[0][j]=0;
if(j<w[i])
V[i][j]=V[i-1][j];
else
V[i][j]=max(V[i-1][j],V[i-1][j-w[i]]+v[i]);
}
}
}
int main(){
B();
//显示填好的表格
for (int i=0;i<5;i++)
{
for(int j=0;j<9;j++)
{
cout<<V[i][j]<<" ";
}
cout<<endl;
}
cout<<"最优结果是:"<<V[4][8];
return 0;
}
下面是带上回溯找出解的组成的代码:
#include<iostream>
using namespace std;
int w[5]={0,2,3,4,5};
int v[5]={0,3,4,5,6};
int V[5][9];
int c=8;
int item[4];
int B()
{
int i,j;
for(i=0;i<5;i++)
{
V[i][0]=0;
for(j=0;j<c+1;j++)
{
V[0][j]=0;
if(j<w[i])
V[i][j]=V[i-1][j];
else
V[i][j]=max(V[i-1][j],V[i-1][j-w[i]]+v[i]);
}
}
}
void FindWhat(int i,int j)//寻找解的组成方式
{
if(i>=0)
{
if(V[i][j]==V[i-1][j])//相等说明没装
{
item[i]=0;//全局变量,标记未被选中
FindWhat(i-1,j);
}
else if( j-w[i]>=0 && V[i][j]==V[i-1][j-w[i]]+v[i] )
{
item[i]=1;//标记已被选中
FindWhat(i-1,j-w[i]);//回到装包之前的位置
}
}
}
int main(){
B();
//显示填好的表格
cout<<"得到的表格如下图所示:"<<endl;
for (int i=0;i<5;i++)
{
for(int j=0;j<9;j++)
{
cout<<V[i][j]<<" ";
}
cout<<endl;
}
cout<<"最优结果是:"<<V[4][8]<<endl;
FindWhat(4,8);
cout<<endl;
cout<<"回溯得到的解是:"<<endl;
for(int i=1;i<5;i++){
if(item[i]==1)
cout<<"背包里面有第"<<i<<"号物品"<<endl;
//cout<<item[i]<<" ";
}
return 0;
}
贴上结果便于理解:
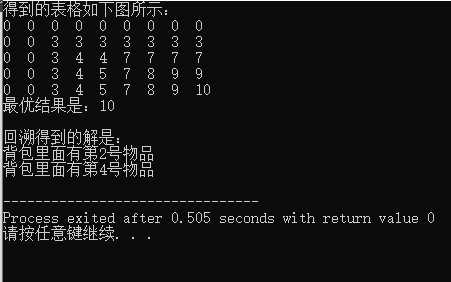
时间复杂度:
O(物体个数*背包容积)=O(number*capacity)
空间复杂度:
用二维表实现的,所以和时间复杂度一样。
O(物体个数*背包容积)=O(number*capacity)
标签:结果 递推 amp 组合 nbsp oid for 变量 htm
原文地址:https://www.cnblogs.com/zhaoxiansheng666/p/12905475.html