标签:如何 img 通过 文法 结果 含义 比较 ati 数值
??word2vec工具主要包含两个模型:跳字模型(skip-gram)和连续词袋模型(CBOW),以及两种高效训练的方法:负采样(negative sampling)和层序softmax(hierarchical softmax)。word2vec词向量可以较好地表达不同词之间的相似和类比关系。
??自然语言是一套用来表达含义的复杂系统。在这套系统中,词是表义的基本单元。在机器学习中,如何使用向量表示词?词向量是用来表示词的向量,通常也被认为是词的特征向量。近年来,词向量已逐渐成为自然语言处理的基础知识。
??NLP(自然语言处理)里面,最细粒度的是词语,词语是符号形式的,所以需要把他们转换成数值形式,嵌入到一个数学空间里,这种嵌入方式,就叫词嵌入,Word2vec,就是词嵌入的一种,简单点来说就是把一个词语转换成对应向量的表达形式,来让机器读取数据。
??统计语言模型给出了这一类问题的一个基本解决框架。对于一段文本序列S=w1,w2...wT,它的概率可以表示为:p(S)=p(w1,w2...wT)=p(w1)p(w2|w1)p(w3|w1,w2)…p(wT|w1,w2,…,wT-1),即将序列的联合概率转化为一系列条件概率的乘积。常见的统计语言模型有N元文法模型(N-gram Model)。
下一个词的出现仅依赖于它前面的一个或几个词。假设下一个词的出现依赖它前面的一个词,则有:p(S)=p(w1)p(w2|w1)p(w3|w1,w2)…p(wn|w1,w2,…,wn-1)=p(w1)p(w2|w1)p(w3|w2)…p(wn|wn-1) // bigram
假设下一个词的出现依赖它前面的两个词,则有:p(S)=p(w1)p(w2|w1)p(w3|w1,w2)…p(wn|w1,w2,…,wn-1)=p(w1)p(w2|w1)p(w3|w1,w2)...p(wn|wn-1,wn-2) // trigram
??那么,我们在面临实际问题时,如何选择依赖词的个数,即n。更大的n:对下一个词出现的约束信息更多,具有更大的辨别力;更小的n:在训练语料库中出现的次数更多,具有更可靠的统计信息,具有更高的可靠性。理论上,n越大越好,经验上,trigram用的最多,尽管如此,原则上,能用bigram解决,绝不使用trigram。
1.one-hot
2.词的分布式表示:基于矩阵的分布表示、基于聚类的分布表示和基于神经网络的分布表示。
主要用到的是CBOW和Skip-gram模型。
??CBOW(Continuous Bag-of-Word Model)又称连续词袋模型,是一个三层神经网络。如下图所示,该模型的特点是输入已知上下文,输出对当前单词的预测。
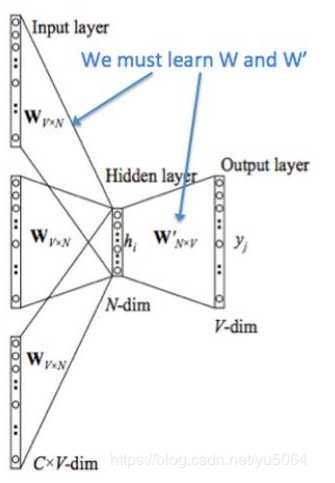
(1)输入层:上下文单词的onehot。(假设单词向量空间dim为V,上下文单词个数为C)
(2)所有onehot分别乘以共享的输入权重矩阵W(VN矩阵,N为自己设定的数,初始化权重矩阵W)
(3)所得的向量 (注意onehot向量乘以矩阵的结果) 相加求平均作为隐层向量, size为1N.
(4)乘以输出权重矩阵W’ {NV}
(5)得到向量 {1V} 激活函数处理得到V-dim概率分布 {PS: 因为是onehot,其中的每一维都代表着一个单词},概率最大的index所指示的单词为预测出的中间词(target word)
(6)与true label的onehot做比较,误差越小越好。loss function(一般为交叉熵代价函数)
??在上图中,这里输入层是由one-hot编码的输入上下文{x1,…,xc}组成,其中窗口大小为C,词汇表大小为V。隐藏层是N维的向量。最后输出层是也被one-hot编码的输出单词y。被one-hot编码的输入向量通过一个V×N维的权重矩阵W连接到隐藏层;隐藏层通过一个N×V的权重矩阵W′连接到输出层。
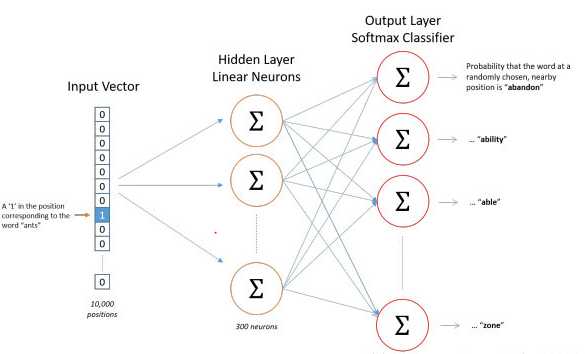
Skip-gram只是逆转了CBOW的因果关系而已,即已知当前词语,预测上下文。
标签:如何 img 通过 文法 结果 含义 比较 ati 数值
原文地址:https://www.cnblogs.com/qiqifan/p/12909419.html