【算法】最短路 - Dijkstra算法

标签：dijkstra   nod   c++   复杂   done   operator   表示   back   img   

Dijkstra算法

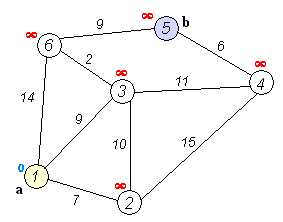
(gif来源：戴克斯特拉算法 - 维基百科)

计算正权图上的单源最短路，同时适用于有向图与无向图

①给源点标记\(d[0]=0\)，其他\(d[i]=INF\)

②循环：每次都从d值最小的结点\(x\)开始，对于从\(x\)出发的所有边\((x,y)\)，对于未被访问过的结点\(y\)，更新\(d[y]=min\{{d[y],d[x]+w(x,y)\}}\)，其中\(w(x,y)\)是边\((x,y)\)的权值。当这些边都访问完毕后，给结点\(x\)标记已访问。

③完成上述操作后的\(d[i]\)即是源点到结点\(i\)的最短路的长度。

//未优化，时间复杂度O(n^2)
void dijkstra() {
	memset(vis, 0, sizeof(vis));
	for (int i = 0; i < n; i++) d[i] = (i == 0 ? 0 : INF);
	for (int i = 0; i <= n; i++) {
		int x, Min = INF;
		for (int y = 0; y < n; y++) {
			if (!v[y] && d[y] <= Min) {
				Min = d[y];
				x = y;
			}
		}
		//遍历所有结点，如果未访问且d值小于当前最小值，则更新
		//遍历完成后x结点是d值最小的
		for (int y = 0; y < n; y++) d[y] = min(d[y], d[x] + w[x][y]);
		v[x] = 1;
		//标记从结点x出发的所有边已访问完毕
	}
}

如果要打印路径，可以用空间换时间，多维护一个“父亲指针”，以便追溯上一结点。

即将d[y]=min(d[y],d[x]+w[x][y])换成

if(d[x] + w[x][y] < d[y]){
	d[y] = d[x] + w[x][y];
	fa[y] = x;
}

这称为边\((x,y)\)上的松弛操作。

对于稀疏图（\(m<<n^2\)），边的表示方式还可以用邻接表或vector数组优化

//用邻接表按顺序存储边
int n, m;
int first[maxn];//first[i]表示结点i的第一条边的编号
int u[maxm], v[maxm], w[maxm],  next[maxm];
//u[e],v[e],w[e],next[e]分别表示边e的两个结点、权值及它的下一条边的编号
cin >> n >> m;
for (int i = 0; i < n; i++) first[i] = -1;//初始化表头
for (int e = 0; e < m; e++) {
    cin >> u[e] >> v[e] >> w[e];
    next[e] = first[u[e]];
    //直接插入链表的头部从而避免遍历，这使得整个表的顺序与边列表的顺序是相反的
    first[u[e]] = e;
    //更新头部指针
}

//vector方法
//用结构体保存边的多种属性，更具扩展性
struct Edge {
	int from, to, dist;
	//边的起点，终点，长度
	Edge(int u,int v,int d):from(u),to(v),dist(d){}
	//构造函数，用于边的初始化
};

struct HeapNode {
	int d, u;//将结点的d值与结点捆绑在一起形成结构体，当然也可以用pair<int,int>代替
	bool operator < (const HeapNode& rhs) const {
		return d > rhs.d;
		//当d>rhs.d为真时，优先级this<rhs.d成立，即d值小的优先级更大
	}
};

struct Dijkstra {
	int n, m;
	vector<Edge> edges;
	vector<int> G[maxn];
	bool done[maxn];//是否已永久标号
	int d[maxn];//源点到各点的距离
	int p[maxn];//最短路中的上一条边

	void init(int n) {//初始化整个图
		this->n = n;
		for (int i = 0; i < n; i++) G[i].clear();
		edges.clear();
	}
	
	void AddEdge(int from, int to, int dist) {
		edges.push_back(Edge(from, to, dist));
		//调用Edge结构体中的构造函数，生成一条边并加入到Edge中
		m = edges.size();
		//m为加入新边后当前已有的总边数，据此给新边编号
		G[from].push_back(m - 1);
		//给这条边编号为m-1（这是为了编号能从0开始）
	}

	void dijkstra(int s){
		priority_queue<HeapNode>Q;
		for (int i = 0; i < n; i++) d[i] = INF;
		d[s] = 0;
		memset(done, 0, sizeof(done));
		Q.push( HeapNode{ 0, s } );
		//HeapNode这个名称不要括起来，否则在VS中会有奇怪的报错
		while (!Q.empty()) {
			HeapNode x = Q.top(); Q.pop();
			//d值最小的结点出队
			int u = x.u;
			//取该结点的起点
			if (done[u]) continue;
			for (int i = 0; i < G[u].size(); i++) {//遍历以u为起点的所有边
				Edge& e = edges[G[u][i]];
				//用G[u][i]取得具体某条边的编号，再用这个编号去找这条边的结构体，获得边的信息
				if (d[u] + e.dist < d[e.to] ) {
					d[e.to] = d[u] + e.dist;
					//更新边的终点的d值
					p[e.to] = G[u][i];
					//松弛操作，即维护最短路中连接这个结点的上一条边的编号
					//注意这里记录的是边而非结点
					Q.push(HeapNode{ d[e.to],e.to });
				}
			}
			done[u] = true;
			//标记起点为u的所有边均已访问
		}
	}
};

【算法】最短路 - Dijkstra算法

标签：dijkstra   nod   c++   复杂   done   operator   表示   back   img   

原文地址：https://www.cnblogs.com/streamazure/p/12918839.html