标签:col view string and 添加 mon round 简单 exp
示例 1:
输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案。
示例 2:
输入: "cbbd"
输出: "bb"
最简单的做法就是暴力解法,通过二重循环确定子串的范围,然后判断子串是不是回文,最后返回最长的回文子串即可。该方法的时间复杂度是O(n^3),空间复杂度是O(1)。

def isPalindromic(s, i, j): j = j-1 # j是右边界,但不包括j while i < j: if s[i] != s[j]: return False i += 1 j -= 1 return True def longestPalindrome(s): lens = len(s) longest = "" for i in range(lens): for j in range(i + 1, lens): if isPalindromic(s, i, j + 1) and j + 1 - i > len(longest): longest = s[i: j + 1] return longest if __name__ == ‘__main__‘: s = "abcba" print(longestPalindrome(s))
中心拓展法的思路是,以原始字符串中的任意一个位置开始(可以是一个字符,也可以是两个字符中间的位置),向两边拓展,如果两边的字母相同,我们就可以继续扩展。例如,用 P(i,j)表示字符串 s 的第 i 到 jj个字母组成的串,从 P(i+1,j-1)扩展到 P(i,j);如果两边的字母不同,我们就可以停止扩展,因为在这之后的子串都不能是回文串了。
时间复杂度:O(n^2),其中 n 是字符串的长度。长度为 1 和 2 的回文中心分别有 n 和 n-1个,每个回文中心最多会向外扩展 O(n)次。
空间复杂度:O(1)。

def expandAroundCenter(s, left, right): while left >= 0 and right < len(s) and s[left] == s[right]: left -= 1 right += 1 return left + 1, right - 1 def longestPalindrome(s): start, end = 0, 0 for i in range(len(s)): left1, right1 = expandAroundCenter(s, i, i) # 奇数 left2, right2 = expandAroundCenter(s, i, i + 1) # 偶数 if right1 - left1 > end - start: start, end = left1, right1 if right2 - left2 > end - start: start, end = left2, right2 return s[start: end + 1] if __name__ == ‘__main__‘: s = "abcba" print(longestPalindrome(s))
对于一个子串而言,如果它是回文串,并且长度大于 22,那么将它首尾的两个字母去除之后,它仍然是个回文串。例如对于字符串 "ababa‘‘,如果我们已经知道"bab" 是回文串,那么"ababa"一定是回文串,这是因为它的首尾两个字母都是"a"。
根据这样的思路,我们就可以用动态规划的方法解决本题。我们用 P(i,j) 表示字符串 s 的第 i 到 j 个字母组成的串(下文表示成 s[i:j])是否为回文串:
$P(i, j)=\left\{\begin{array}{ll}\text { true, } & \text { 如果子串 } S_{i} \ldots S_{j} \text { 是回文串 } \\ \text { false, } & \text { 其它情况 }\end{array}\right.$
这里里的「其它情况」包含两种可能性:
那么我们就可以写出动态规划的状态转移方程:
$P(i, j)=P(i+1, j-1) \wedge\left(S_{i}==S_{j}\right)$
也就是说,只有 s[i+1:j-1]是回文串,并且 ss的第 i 和 j 个字母相同时,s[i:j] 才会是回文串。
上文的所有讨论是建立在子串长度大于 2 的前提之上的,我们还需要考虑动态规划中的边界条件,即子串的长度为 1 或 2。对于长度为 1 的子串,它显然是个回文串;对于长度为 2 的子串,只要它的两个字母相同,它就是一个回文串。因此我们就可以写出动态规划的边界条件:
$
\left\{\begin{array}{l}
P(i, i)=\text { true } \\
P(i, i+1)=\left(S_{i}==S_{i+1}\right)
\end{array}\right.
$
根据这个思路,我们就可以完成动态规划了,最终的答案即为所有 P(i, j) = true 中 j-i+1 即子串长度)的最大值。注意:在状态转移方程中,我们是从长度较短的字符串向长度较长的字符串进行转移的,因此一定要注意动态规划的循环顺序。

# -*- coding:utf-8 -*- def longestPalindrome(s: str) -> str: n = len(s) dp = [[False] * n for _ in range(n)] res = "" # 枚举子串的长度 l+1 for l in range(n): # 枚举子串的起始位置 i,这样可以通过 j=i+l 得到子串的结束位置 for i in range(n): j = i + l if j >= len(s): break if l == 0: dp[i][j] = True elif l == 1: dp[i][j] = (s[i] == s[j]) else: dp[i][j] = (dp[i + 1][j - 1] and s[i] == s[j]) if dp[i][j] and l + 1 > len(res): res = s[i:j+1] return res if __name__ == ‘__main__‘: s = "cbaabcbd" strs = longestPalindrome(s) print(strs)
首先,为了便于处理,通过在字符串中添加#将字符串统一转换成奇数长度。处理方式:在字符串中每个字符的两边添加#
比如字符串 aaba 处理后会变成 #a#a#b#a#。那么原先长度为偶数的回文字符串 aa 会变成长度为奇数的回文字符串 #a#a#,而长度为奇数的回文字符串 aba 会变成长度仍然为奇数的回文字符串 #a#b#a#,我们就不需要再考虑长度为偶数的回文字符串了。注意这里的特殊字符不需要是没有出现过的字母,我们可以使用任何一个字符来作为这个特殊字符。这是因为,当我们只考虑长度为奇数的回文字符串时,每次我们比较的两个字符奇偶性一定是相同的,所以原来字符串中的字符不会与插入的特殊字符互相比较,不会因此产生问题。当然,为了后续方便还原子串,还是建议使用未出现的字符。
在这一步中,要定义几个变量和数组,R,c,maxLenS和数组RArr 。含义如下:
RArr :RArr [i]表示,以i为中心的回文串的半径。(则以i为中心的回文长度是RArr [i]-1)
c = -1 # 延伸到边界r的回文串的中心为c
R = -1 # 回文右边界的再往右一个位置,最右的有效区是R-1位置
maxLenS = 0 # 扩出来的最大半径
例如,给定一个字符串:cbaabcbd,处理后,s_new:#c#b#a#a#b#c#b#d#
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| s_new | # | c | # | b | # | a | # | a | # | b | # | c | # | b | # | d | # |
| RArr[i] | 1 | 2 | 1 | 2 | 1 | 2 | 7 | 2 | 1 | 2 | 1 | 4 | 1 | 2 | 1 | 2 | 1 |
可以看出,RArr[i] - 1正好是原字符串中最长回文串的长度。
如下图
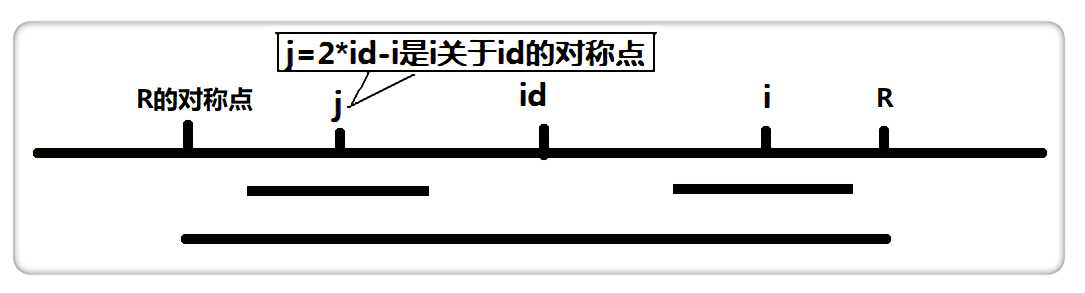
设置两个变量,R 和 id 。mx 代表以 id 为中心的最长回文的右边界,也就是R = id + p[id]。
假设我们现在求p[i],也就是以 i 为中心的最长回文半径,如果i < R,如上图,那么,对于第i个位置,回文半径至少为:
if R < i: RArr[i] = 1 else: RArr[i] = min(RArr[2 * id - i], R - i)
(2 * id - i)为 i 关于 id 的对称点,即上图的 j 点,而RArr[j]表示以 j 为中心的最长回文半径,因此我们可以利用RArr[j]来加快查找。
a. 首先,如果 i 在右边界外面,显然 RArr[i] 的值至少为1,因为左右两边都是相同字符 ”#“ ,要看RArr[i]真实半径,往两边遍历比较即可
b. j 的回文串有一部分在 id 的之外,如下图:
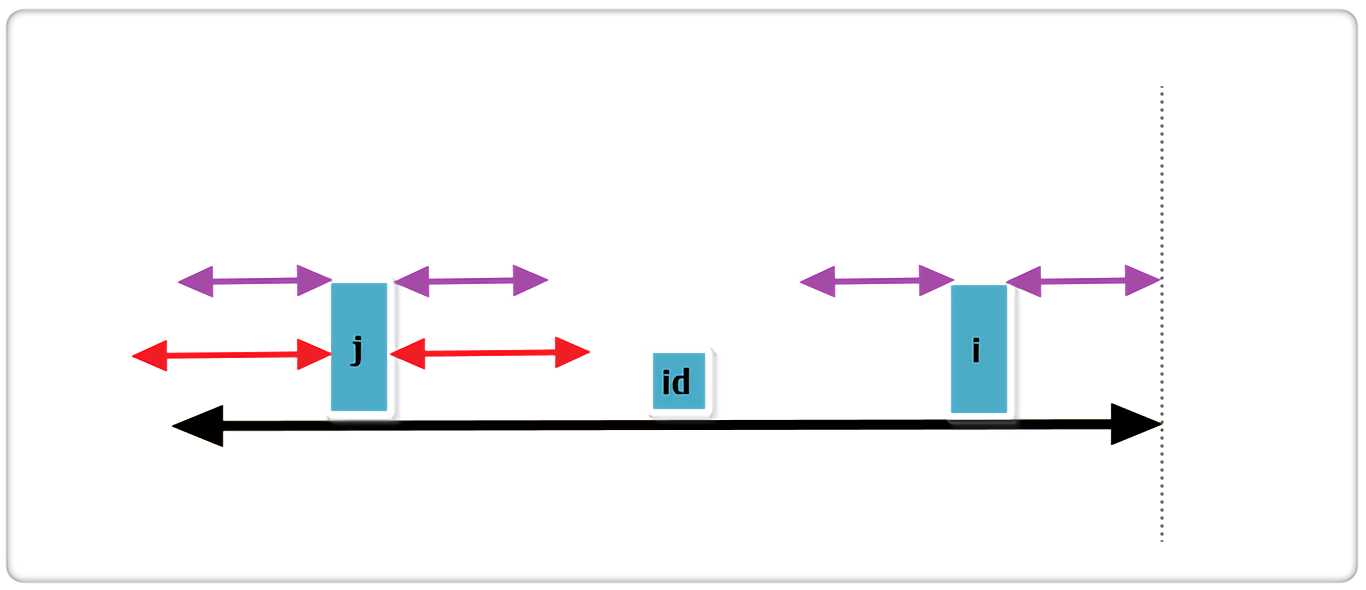
上图中,黑线为 id 的回文,i 与 j 关于 id 对称,红线为 j 的回文。那么根据代码此时RArr[i] = R - i,即紫线。那么p[i]还可以更大么?答案是不可能!见下图:
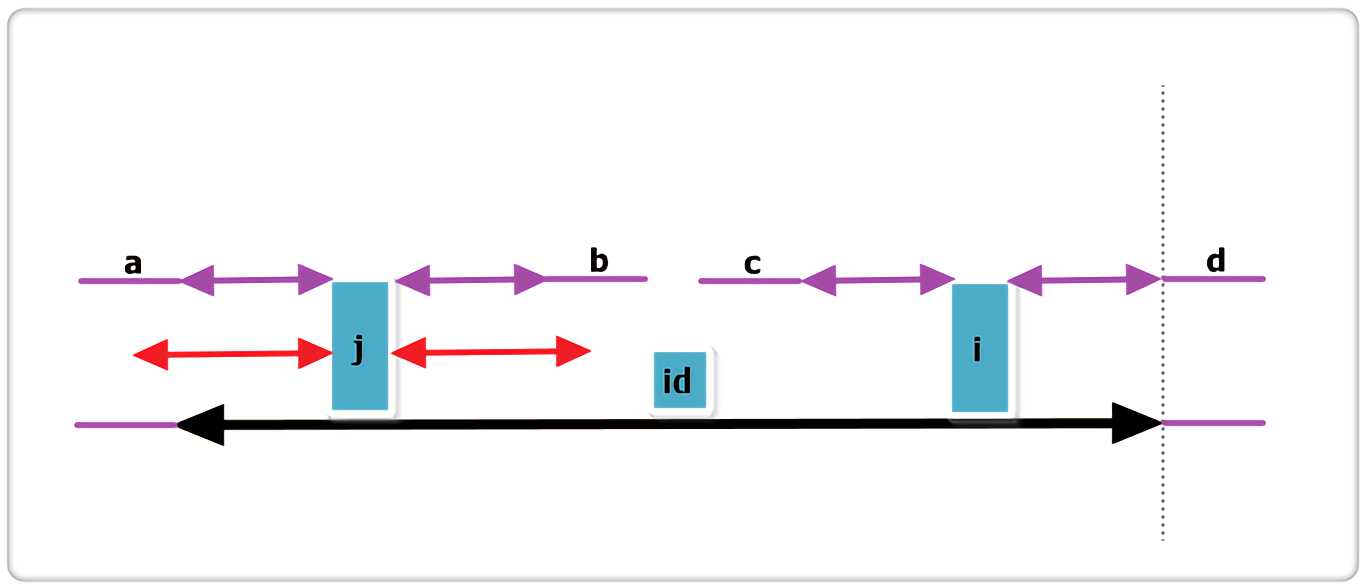
假设右侧新增的紫色部分是RArr[i]可以增加的部分,那么根据回文的性质,a 等于 d ,也就是说 id 的回文不仅仅是黑线,而是黑线+两条紫线,矛盾,所以假设不成立,故p[i] = R - i,不可以再增加一分。
c. j 回文串全部在 id 的内部,如下图:
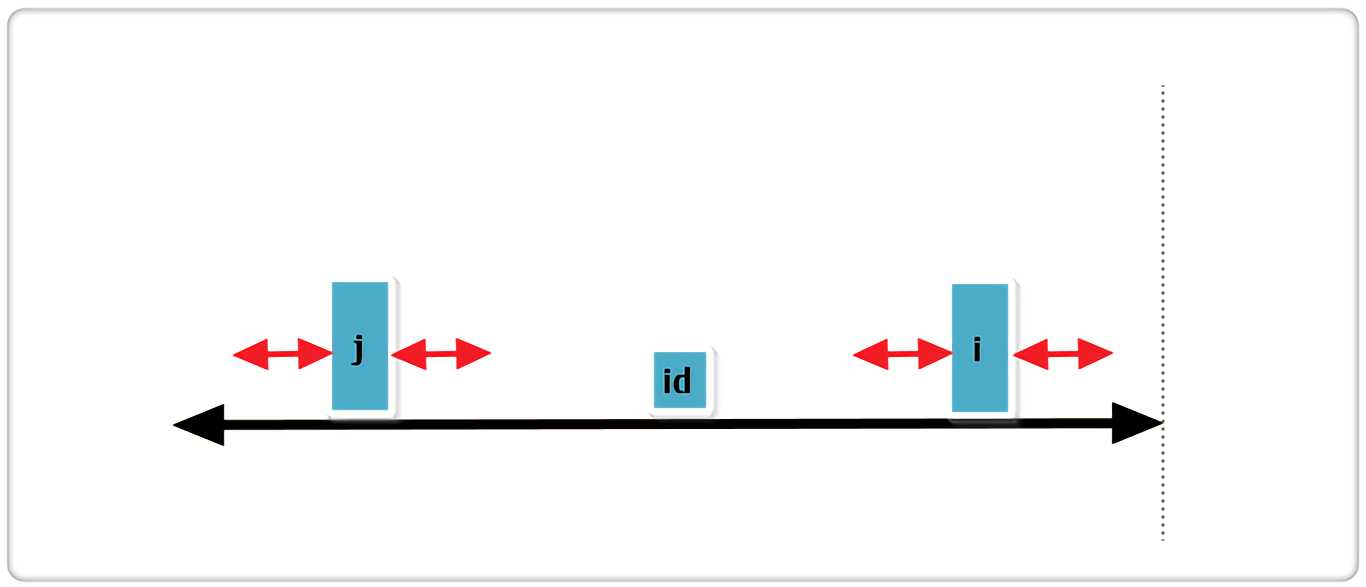
根据代码,此时RArr[i] = RArr[j],那么RArr[i]还可以更大么?答案亦是不可能!见下图:
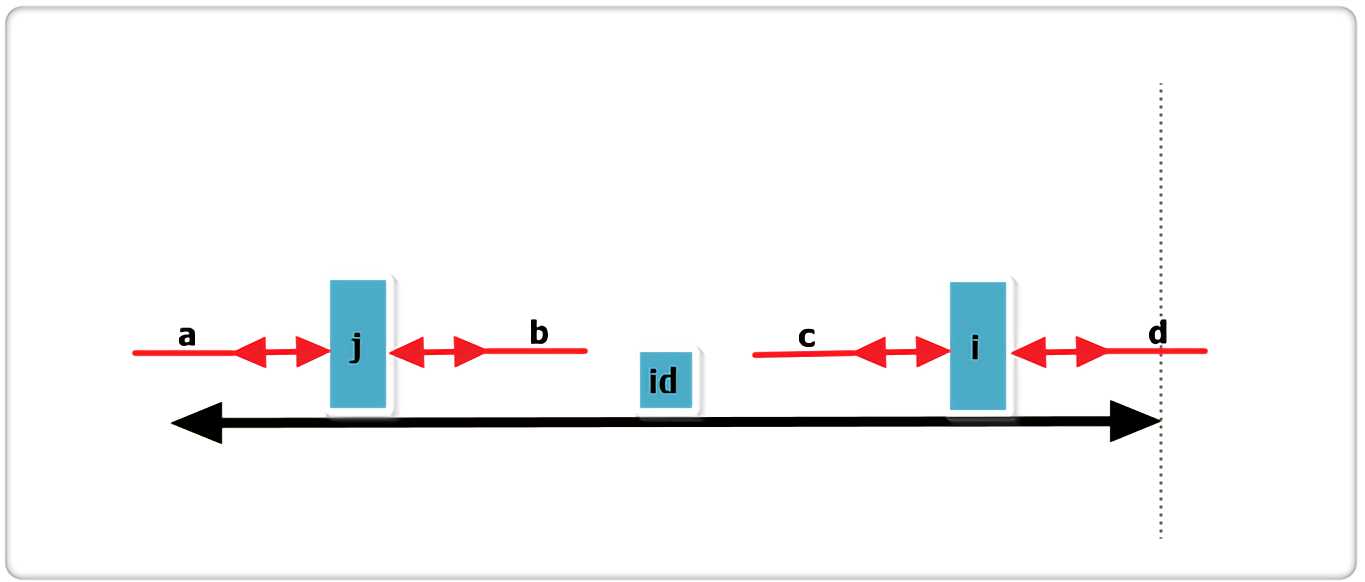
假设右侧新增的红色部分是RArr[i]可以增加的部分,那么根据回文的性质,a 等于 b ,也就是说 j 的回文应该再加上 a 和 b ,矛盾,所以假设不成立,故RArr[i] = RArr[j],也不可以再增加一分。
d. j 回文串左端正好与 id 的回文串左端重合,见下图:
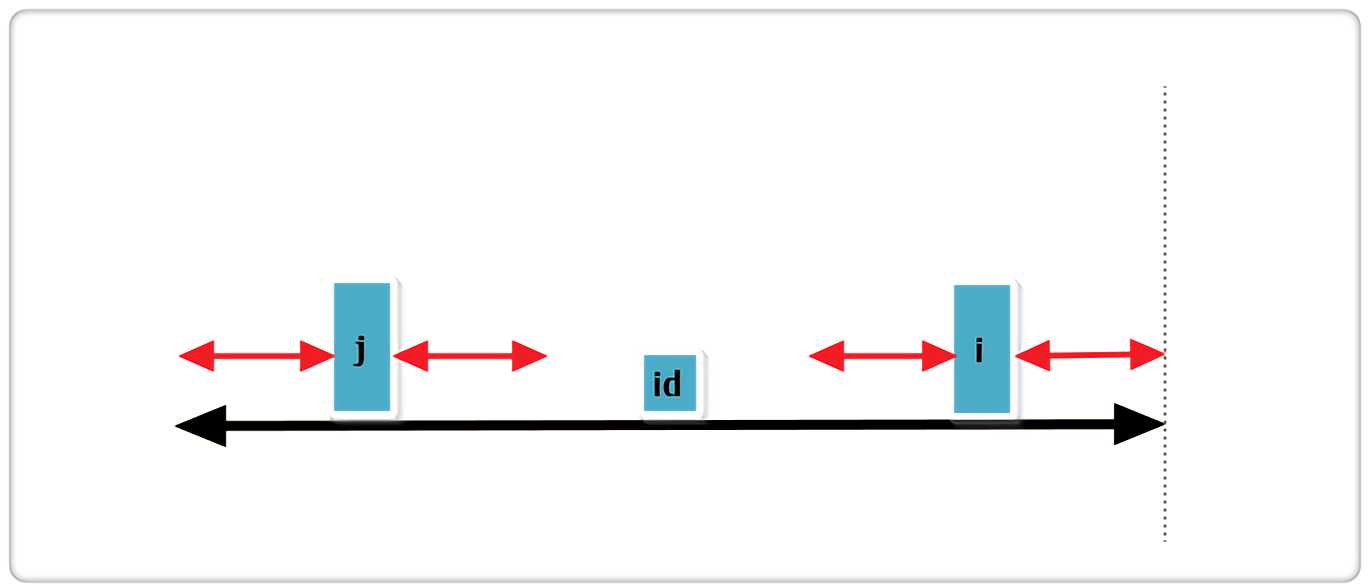
根据代码,此时RArr[i] = RArr[j]或RArr[i] = R - i,并且RArr[i]还可以继续增加。例如,考虑如下,当右边界下一个字符为T时,半径加一,否则,半径即为R - i

综合上述情况,半径处理代码如下:
# i至少的回文区域,给pArr[i] if R < i: RArr[i] = 1 else: RArr[i] = min(RArr[2 * c - i], R - i) # 1,4种情况,看半径能否扩增;2,3种情况,直接break while (i + RArr[i]) < len(s) and (i - RArr[i]) > -1: if s[i + RArr[i]] == s[i - RArr[i]]: RArr[i] += 1 else: break

# -*- coding:utf-8 -*- def manacherStr(s): return "#" + "#".join(s) + "#" def manacher(s): if not s: return 0 s = manacherStr(s) RArr = [0 for _ in range(len(s))] # 回文半径数组 c = -1 # 中心点 R = -1 # 回文右边界的再往右一个位置最右的有效区是R-1位置 maxLenS = 0 # 扩出来的最大半径 for i in range(len(s)): # 每一个位置都求回文半径 # i至少的回文区域,给pArr[i] if R < i: RArr[i] = 1 else: RArr[i] = min(RArr[2 * c - i], R - i) # 1,4种情况,看半径能否扩增;2,3种情况,直接break while (i + RArr[i]) < len(s) and (i - RArr[i]) > -1: if s[i + RArr[i]] == s[i - RArr[i]]: RArr[i] += 1 else: break # 边界>R,更新R和c if i + RArr[i] > R: R = i + RArr[i] c = i maxLenS = max(maxLenS, RArr[i]) s = s[RArr.index(maxLenS) - (maxLenS - 1) :RArr.index(maxLenS) + (maxLenS - 1)] s = s.replace(‘#‘, ‘‘) maxstrlens = maxLenS - 1 # 最大长度 maxstr = s # 最长回文子串 return maxstr if __name__ == ‘__main__‘: s = "cbaabcbd" maxstr = manacher(s) print(maxstr)
最大回文子串匹配:暴力算法、中心拓展法、动态规划、manacher算法
标签:col view string and 添加 mon round 简单 exp
原文地址:https://www.cnblogs.com/r1-12king/p/12929965.html