堆排序实现

标签：利用   mic   var   src   static   int   上进   while   父节点   

什么是堆

堆是一个近似完全二叉树的结构，

并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

什么是堆排序

堆排序（英语：Heapsort）是指利用堆这种数据结构所设计的一种排序算法。

实现大顶堆

首先我们需要找到所有的非叶子结点，通过完全二叉树的性质我们知道

若父节点标号为n，则他的左结点为n×2，右结点为n×2+1

也就是说，当前所存储的最后一位数据的下标位置就是最后一个非叶子节点的孩子结点，逆推得出最后一个非叶子结点的下标为

Arr是我们所存储数据的容器。

得到所有的非叶子结点后，我们需要对每一个非叶子结点和他的孩子结点进行比较大小，使它们都变成子大顶堆。

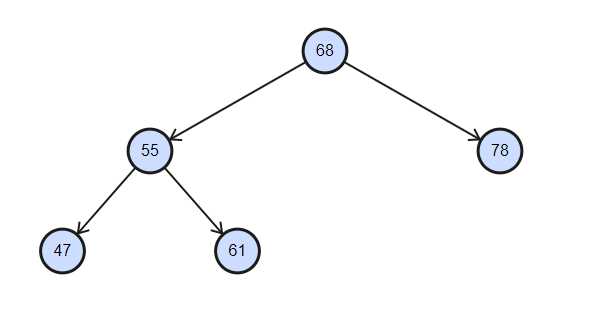
在上图中，我们能看出 55、68结点是非叶子结点，我们进行堆排序的时候是从下晚上进行堆排序。

首先，对55的节点和他的孩子结点进行排序，好，没有问题，接下来对68结点和他的孩子进行排序。

这时候出现一个问题：

如果对68结点进行排序的时候，被换到原本55结点所在的位置，且比此时他的孩子结点的值还要小怎么办？

所以我们只能继续进行排序，在对上一层进行排序的时候，如果被换到下级的子大顶堆的时候，此时就不一定还能继续构成子大顶堆，所以需要对之前的子节点重新进行排序。

实现代码如下：

static void HeapSort(int[] data)
        {
            for (int i = data.Length / 2; i >= 1; i--) 
            {
                int MaxNodeData = i;
                int var = i;
                while (true)
                {
                    int LeftNodeNumber = var * 2;
                    int RightNodeNumber = LeftNodeNumber + 1;

                    if(LeftNodeNumber <= data.Length && data[LeftNodeNumber -1] > data[var - 1])
                    {
                        MaxNodeData = LeftNodeNumber;
                    }
                    if (RightNodeNumber <= data.Length && data[RightNodeNumber - 1] > data[var - 1] && data[MaxNodeData - 1] < data[RightNodeNumber - 1])
                    {
                        MaxNodeData = RightNodeNumber;
                    }

                    if(MaxNodeData != var)
                    {
                        int temp = data[var - 1];
                        data[var - 1] = data[MaxNodeData - 1];
                        data[MaxNodeData - 1] = temp;
                        var = MaxNodeData;
                    }
                    else
                    {
                        break;
                    }
                }
            }

堆排序实现

标签：利用   mic   var   src   static   int   上进   while   父节点   

原文地址：https://www.cnblogs.com/lehanbal/p/12943621.html