标签：时间复杂度   fine   堆排   示意图   png   names   伪代码   nlog   ima   

题目1–前k大问题

题目：从一组元素（n个）中找出前k大个元素。

这题和PTA 7-5 选做 寻找大富翁差不多，7-5的提交情况：

代码

代码：

#include<iostream>
#define MaxNum 1000001 
using namespace std;
int arr[MaxNum];
void sift(int R[], int low, int high) {
	int i = low, j = i * 2;
	int tmp = R[i];
	while (j <= high) {
		if (j < high && R[j] < R[j + 1]) j++;
		if (tmp < R[j]) {
			R[i] = R[j];
			i = j;
			j = 2 * i;
		}
		else break;
	}
	R[i] = tmp;
}
void Heap(int R[], int n, int m) {
	int i, j, t;
	for (i = n / 2; i >= 1; i--)
		sift(R, i, n);
	for (i = n, j = 0; i >= 2, j < m; i--, j++) {
		t = R[1];
		R[1] = R[i];
		R[i] = t;
		sift(R, 1, i - 1);
	}
}


int main() {
	int n, m;
	scanf("%d %d", &n, &m);
	for (int i = 1; i <= n; i++) {
		scanf("%d", &arr[i]);
	}
	if (m > n) m = n;
	Heap(arr, n, m);
	
	for (int i = n, j = 1; j <= m; j++, i--) {
		cout << arr[i];
		if (j < m) cout << " ";
	}
}

考核点

给出方法描述或示意图

方法描述：输入n和k，随后输入n个整数，利用堆排序每趟产生的有序区一定是全局有序区（即每趟产生的有序区中的所有元素都归位了）且每次挑选最大元素归位的性质，用改造后的堆排序对数组进行排序，最后输出前k大元素。
堆排序首先要构建初始堆，在初始堆R[1..n]构造好后，根节点R[1]一定是最大元素，将其放到排序序列的最后，也就是将堆中的根与最后一个叶子结点交换。由于最大元素已归位，整个待排序的元素个数将减少一个。由于根节点的改变，这n-1个结点R[1..n-1]不一定为堆，但其左右子树均为堆，再调用一次sift函数将这n-1个结点R[1..n-1]调整成堆，其根节点为次大的元素，将它放到排序序列的倒数第2个位置，即将堆中的根与最后一个叶子结点交换，待排序的元素个数变为n-2个，即R[1..n-2]，再调整，再将根节点归位，如此这样，直到归位了k个元素为止。

预估方法时间复杂度、空间复杂度

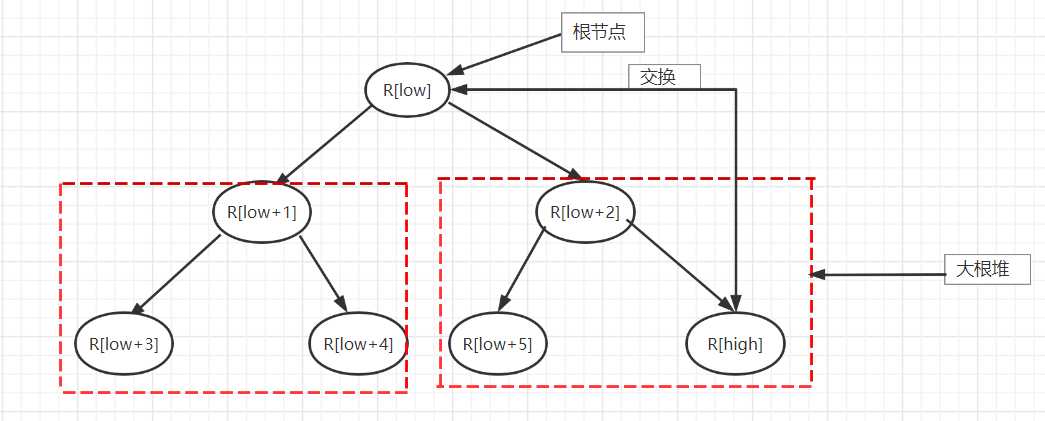
堆排序的时间复杂度为O(nlog2(n)),但这个方法并不用进行n-1趟排序，所以预估平均时间复杂度应该略好与O(nlog2(n))
堆排序仅使用i、j、tmp等辅助变量，所用空间为数组的大小，所以空间复杂度为O(n),辅助空间复杂度为(1)

尝试给出伪代码

void sift(RecType R[], int low, int high) {
	int i = low, j = i * 2;//R[j]是R[i]的左孩子
	RecType tmp = R[i];
	while (j 小于 high) {
		if (j 小于 high && 右孩子比左孩子大) j指向右孩子j++;
		if (根节点 小于 最大孩子) {
			将R[j]调整到双亲结点位置上;
			修改i和j值，以便继续向下筛选;

		}
		else 若根节点大于等于最大孩子，筛选结束;
	}
	被筛选结点放入最终位置上;
}
void Heap(RecType R[], int n, int k) {
	int i, j;
	RecType t;
	for (i = n / 2; i >= 1; i--)//循环建立初始堆，调用sift函数n/2次
		sift(R, i, n);
	for (i = n, j = 0; i >= 2 && j < k; i--, j++) {
		将最后一个元素与根R[1]交换;
		对R[1...i - 1]进行筛选，得到i - 1个结点的堆;
	}
}
int main() {
	int n, k;
	输入n和k;
	for (int i = 1; i <= n; i++) {
		输入n个元素，存放在arr数组中;
	}
	if (k 大于 n) k = n;
	Heap(arr, n, k);

	for (int i = n, j = 1; j <= k; j++, i--) {
		从数组后往前输出k个元素;
		if (j 小于 k) cout << " ";
	}
}

排序 专题讨论

标签：时间复杂度   fine   堆排   示意图   png   names   伪代码   nlog   ima   

原文地址：https://www.cnblogs.com/cjt0722/p/12951620.html