标签：tip   复杂度   排序   渐进   传递   lock   复习   ESS   pre   

之前想开坑坚持实践陈皓的ARTS挑战, 奈何发现自己的学习水平和输出水平做不到写一篇ARTS文章. 不过我很喜欢ARTS的写作方向: Algorithm(算法), Review(评论), Tip(实践技巧), Share/Study(分享/学习); 这四方面相辅相成, 能够通过写作很好的锻炼各项能力. 所以, 就拆分一下吧, 1次写不了4个, 那1次写1个还是可以的.

定义

算法的时间复杂度使用渐进记号(\(\Theta\), \(O\), \(\Omega\), \(o\), \(\omega\))来描述, 它们的定义如下:

这些渐进记号中平常常用的是前三种(\(\Theta\), \(O\), \(\Omega\)), 因为日常使用中我们最关心最坏情况下时间复杂度, 所以渐进上界\(O\)也是最为常用的记号. 对于这三种记号, 结合算法导论上的配图很好理解.

1. \(O\)描述了最坏情况下的时间复杂度量级;
2. \(\Omega\)描述了最好情况下的时间复杂度量级;
3. \(\Theta\)是由\(O\)和\(\Omega\)组成的一个区间;

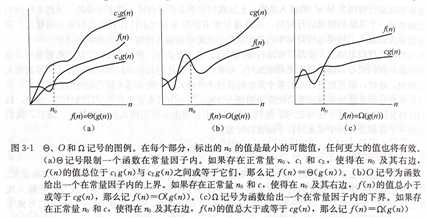
将渐进记号和实数之间的大小比较作类比, 也更好理解:

运算

渐进函数具有传递性, 自反性, 对称性和转置对称性. 举例来说:

利用这些性质可以通过推导的方式得出算法的时间复杂度.

• 以快速排序为例

# 提供一个最好理解的递归实现
# https://www.jianshu.com/p/2b2f1f79984e
def quick_sort(array):
    if len(array) < 2:
        return array
    else:
        pivot = array[0]
        less_than_pivot = [x for x in array if x <= pivot]
        more_than_pivot = [x for x in array if x > pivot]
        return quick_sort(less_than_pivot) + [pivot] + quick_sort(more_than_pivot)

时间复杂度推导公式如下:

• 附上不同算法复杂度的增长趋势:
  https://www.geogebra.org/calculator/brd6wjte
  

[Study] 算法时间复杂度计算方法复习

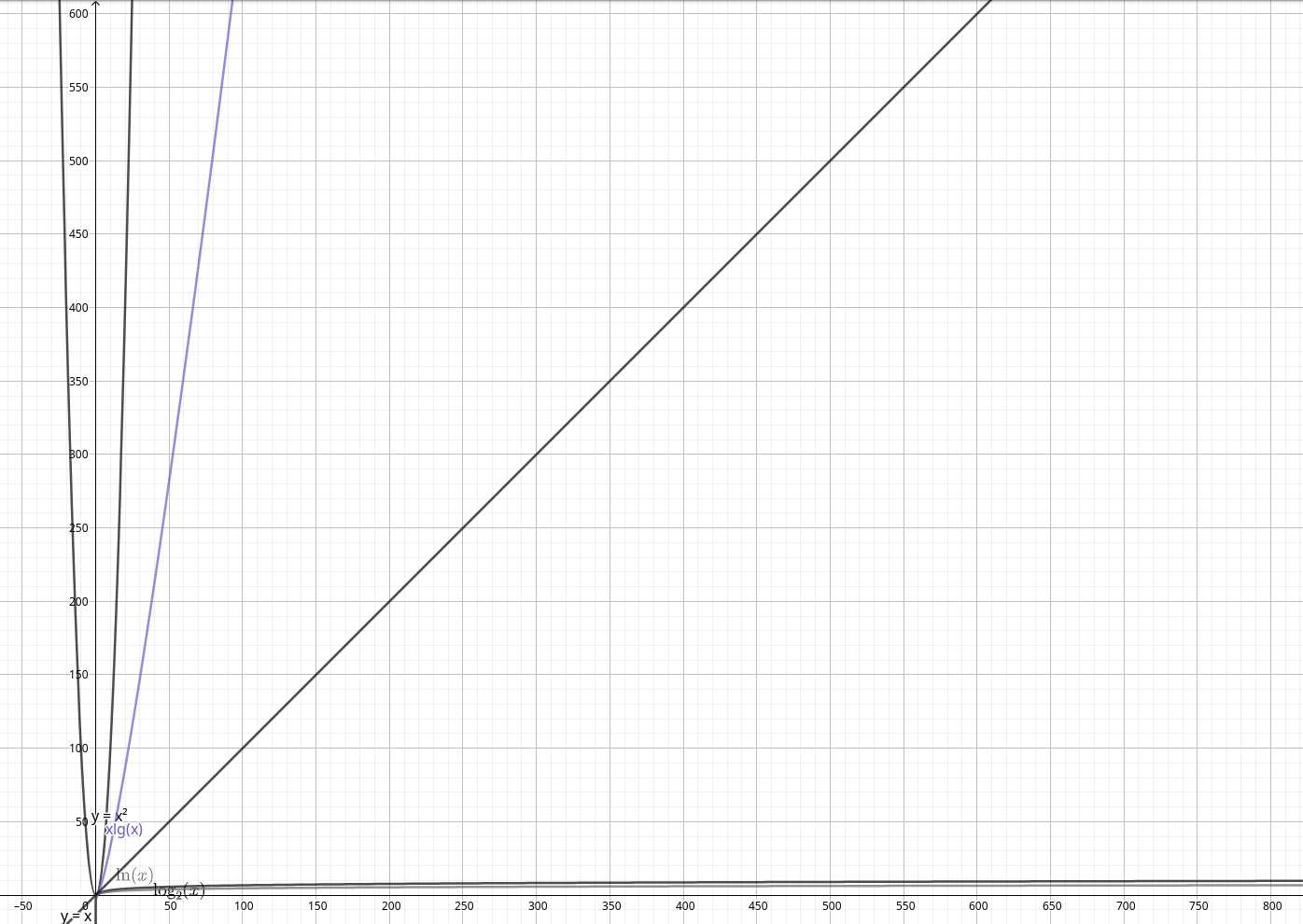
标签：tip   复杂度   排序   渐进   传递   lock   复习   ESS   pre   

原文地址：https://www.cnblogs.com/carlsplace/p/12951334.html