标签:根据 char i++ rank void mini sed string 邻接矩阵
PageRank让链接来"投票"
一个页面的“得票数”由所有链向它的页面的重要性来决定,到一个页面的超链接相当于对该页投一票。一个页面的PageRank是由所有链向它的页面(“链入页面”)的重要性经过递归算法得到的。一个有较多链入的页面会有较高的等级,相反如果一个页面没有任何链入页面,那么它没有等级。
2005年初,Google为网页链接推出一项新属性nofollow,使得网站管理员和网站作者可以做出一些Google不计票的链接,也就是说这些链接不算作"投票"。nofollow的设置可以抵制评论垃圾。
假设一个由4个页面组成的小团体:A,B,C和D。如果所有页面都链向A,那么A的PR(PageRank)值将是B,C及D的Pagerank总和。
继续假设B也有链接到C,并且D也有链接到包括A的3个页面。一个页面不能投票2次。所以B给每个页面半票。以同样的逻辑,D投出的票只有三分之一算到了A的PageRank上。
换句话说,根据链出总数平分一个页面的PR值。
最后,所有这些被换算为一个百分比再乘上一个系数。由于“没有向外链接的页面”传递出去的PageRank会是0,所以,Google通过数学系统给了每个页面一个最小值:
说明:在Sergey Brin和Lawrence Page的1998年原文中给每一个页面设定的最小值是1-d,而不是这里的
(1-d)/N。 所以一个页面的PageRank是由其他页面的PageRank计算得到。Google不断的重复计算每个页面的PageRank。如果给每个页面一个随机PageRank值(非0),那么经过不断的重复计算,这些页面的PR值会趋向于稳定,也就是收敛的状态。这就是搜索引擎使用它的原因。
实验数据a.txt是小的随机生成的图(图中没有终止点)。节点个数n=1000,边数m=8192
该图有一个1000条边构成的有向环(遍历了所有的节点),这确保了该图是连通的。显然,这样的一个有向环确保了该图中没有终止点(即任何一个点都有出边)。如果存在一对节点之间有多条相同的有向边,你的算法应该把它们当做是同一条边。a.txt的每一行表示一条有向边,第一列表示边的源结点,第二列表示边的目的节点。
l 实现过程:
设有向图 G=(V,E)有n个节点(编号为1,2,...N)和M条边,所有的节点都有至少一个出边,且M=[Mji](n*n)是一个m*n的随机邻接矩阵,定义如下:对任意i,j€[1,n]
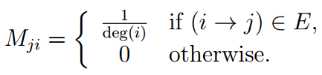
里,deg(i)是图G中节点i的出边个数。基于PageRank的定义,设1-Β为随机跳转概率,我们将PageRank向量记为r,有如下等式
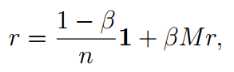
基于上面的公式,计算PageRank向量的迭代过程如下:
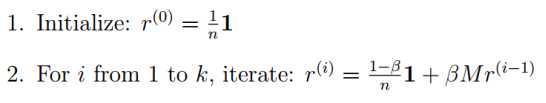
矩阵运算调用了 MathNet.Numerics

1 public static double[,] Get() 2 { 3 double[,] m = new double[1000, 1000]; 4 for (int i = 0; i < 1000; i++) 5 { 6 for (int j = 0; j < 1000; j++) 7 { 8 m[i, j] = 0; 9 } 10 } 11 double[] s = new double[1000]; 12 double[,] M = new double[1000, 1000]; 13 for (int i = 0; i < 1000; i++) 14 { 15 for (int j = 0; j < 1000; j++) 16 { 17 M[i, j] = 0; 18 } 19 20 } 21 StreamReader sr = File.OpenText(@"E:\a.txt"); 22 string nextLine; 23 while ((nextLine = sr.ReadLine()) != null) 24 { 25 char[] charTemp = { ‘\t‘ }; 26 string[] arr = nextLine.Split(charTemp); 27 int[] d = Array.ConvertAll(arr, int.Parse); 28 int a1 = d[0] - 1; 29 int a2 = d[1] - 1; 30 m[a1, a2] = 1; 31 } 32 sr.Close(); 33 for (int i = 0; i < 1000; i++) 34 { 35 for (int j = 0; j < 1000; j++) 36 { 37 s[i] += m[i, j]; 38 } 39 } 40 for (int i = 0; i < 1000; i++) 41 { 42 for (int j = 0; j < 1000; j++) 43 { 44 if (m[i, j] == 1) 45 M[j, i] = 1.0 / s[i]; 46 } 47 } 48 return M; 49 } 50 public static double [] Getmtrix(double[,] M) 51 { 52 53 double num = 0.8; 54 double[,] result = Get(); 55 var mb = Matrix<double>.Build; 56 var A= mb.DenseOfArray(result); 57 var matrixR = mb.Dense(1000, 1, 0.001); 58 var matrixL = mb.Dense(1000, 1, 0.0002); 59 for (int p = 0; p < 40; p++) 60 { 61 matrixR = matrixL + (A * matrixR) * num; 62 } 63 double[,]b= matrixR.ToArray(); 64 double[] d = new double[b.Length]; 65 for (int i = 0; i < b.Length; i++) 66 { 67 for (int j = 0; j < 1; j++) 68 { 69 d[i] = b[i, j]; 70 } 71 } 72 return d; 73 } 74 public static void show(double[] a) 75 { 76 double[] a1 = Getmtrix(Get()); 77 double max = 1; 78 int maxindex = -1; 79 for (int j = 0; j < 5; j++) 80 { 81 max = a1.Max(); 82 maxindex = Array.IndexOf(a1, max); 83 a1[maxindex] = 0; 84 Console.WriteLine("最大:{0}" + "节点:{1}", j+1, maxindex+1); 85 86 } 87 88 } 89 public static void show2(double[] a) 90 { 91 double[] a1 = Getmtrix(Get()); 92 for (int j = 0; j < 5; j++) 93 { 94 double min = 1.0; 95 int minindex = -1; 96 min = a1.Min(); 97 minindex = Array.IndexOf(a1, min); 98 a1[minindex] = 1; 99 Console.WriteLine("最小:{0}" + "节点:{1}", j + 1, minindex + 1); 100 } 101 Console.ReadKey(); 102 } 103 static void Main(string[] args) 104 { 105 show(Getmtrix(Get())); 106 show2(Getmtrix(Get())); 107 108 }
l 输出
ü PageRank分值最高的5个节点的id
ü PageRank分值最低的5个节点的id
l graph-full.txt
标签:根据 char i++ rank void mini sed string 邻接矩阵
原文地址:https://www.cnblogs.com/amazing-ld/p/13022290.html