标签:get 返回 性能 复杂 math 数组 结果 等于 bilibili
最近又遇到快速排序算法了,才发现以前学的那种快速排序算法有问题,在此记录一下两种不同快速排序算法的性能比较
思路:
①选择数组中间数作为基数,并从数组中取出此基数
②准备两个新数组容器,遍历数组,逐个与基数比对,较小的放左边容器,较大的放右边容器
③递归处理两个容器的元素,并将处理后的数据与基数按大小合并成一个数组,返回
实现:
// 方法一 function quick_1(ary) { //4.结束递归(当ARY中小于等于一项,则不用处理) if (ary.length <= 1) { return ary } // 1.找到数组的中间项,在原有的数组中把它移除 let middleIndex = Math.floor(ary.length / 2) let middleValue = ary.splice(middleIndex, 1)[0] //2.准备左右两个数组,循环剩下数组中的每一项,比当前项小的放到左边数组中,反之放到右边数组当中 let aryLeft = [], aryRight = [] for (let i = 0; i < ary.length; i++) { ary[i] < middleValue ? aryLeft.push(ary[i]) : aryRight.push(ary[i]) } //3.递归方式让左右两边的数组持续这样处理,一直到左右两边都排好序为止(最后让左边+中间+右边拼接成为最后的结果) return quick_1(aryLeft).concat(middleValue, quick_1(aryRight)) }
缺点:
①调用函数删除基数会更耗时
②专门生成两个数组来存储,增加了空间复杂度
思路:
①选定pivot中心轴
②设定两个下标L和R,不断从右向左移动R下标,一旦发现比pivot小的数字,则把该数字放到L所指的位置;然后不断向右移动L下标,一旦发现比pivot大的数字,则把该数字放到R所指的位置;然后从右向左移动R下标,重复执行之前的步骤,直到L等于R,结束第一次排序
③分别对左右子序列重复前两步操作
实现:
// 方法二 function quick_2(arry) { return quick(arry, 0, arry.length - 1) } function quick(arry, L, R) { if (L >= R) return let left = L let right = R let pivot = arry[left] while (left < right) { while (left < right && arry[right] >= pivot) { right-- } if (left < right) { arry[left] = arry[right] } while (left < right && arry[left] <= pivot) { left++ } if (left < right) { arry[right] = arry[left] } if (left >= right) { arry[left] = pivot } } quick(arry, L, right - 1) quick(arry, right + 1, R) }
优点:
①利用双指针移动下标取数,更快
②不需要创建新数组存储被划分的数据,降低了空间复杂度
测试:
选取100000个随机整数,利用两种不同思路的快速排序方法进行性能测试
// 方法一 function quick_1(ary) { //4.结束递归(当ARY中小于等于一项,则不用处理) if (ary.length <= 1) { return ary } // 1.找到数组的中间项,在原有的数组中把它移除 let middleIndex = Math.floor(ary.length / 2) let middleValue = ary.splice(middleIndex, 1)[0] //2.准备左右两个数组,循环剩下数组中的每一项,比当前项小的放到左边数组中,反之放到右边数组当中 let aryLeft = [], aryRight = [] for (let i = 0; i < ary.length; i++) { ary[i] < middleValue ? aryLeft.push(ary[i]) : aryRight.push(ary[i]) } //3.递归方式让左右两边的数组持续这样处理,一直到左右两边都排好序为止(最后让左边+中间+右边拼接成为最后的结果) return quick_1(aryLeft).concat(middleValue, quick_1(aryRight)) } // 方法二 function quick_2(arry) { return quick(arry, 0, arry.length - 1) } function quick(arry, L, R) { if (L >= R) return let left = L let right = R let pivot = arry[left] while (left < right) { while (left < right && arry[right] >= pivot) { right-- } if (left < right) { arry[left] = arry[right] } while (left < right && arry[left] <= pivot) { left++ } if (left < right) { arry[right] = arry[left] } if (left >= right) { arry[left] = pivot } } quick(arry, L, right - 1) quick(arry, right + 1, R) } // 生成num个m到n范围内的随机整数 function getRandom(m, n, num) { let list = [] for (let i = 0; i < num; i++) { let random = Math.floor(Math.random() * (n - m) + m) list.push(random) } return list } let ary = getRandom(1, 100000, 100000) let ary1 = [...ary] let ary2 = [...ary] console.time(‘quick_1‘) quick_1(ary1) console.timeEnd(‘quick_1‘) console.time(‘quick_2‘) quick_2(ary2) console.timeEnd(‘quick_2‘)
测试结果:(在谷歌浏览器上测试)
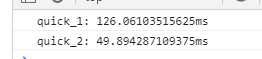
结论:
方法二实现排序更快速更省空间
https://www.cnblogs.com/hjx-blog/articles/9183453.html
https://www.bilibili.com/video/BV1at411T75o?from=search&seid=11059659226640382451
https://www.bilibili.com/video/BV1YE411a7zK
标签:get 返回 性能 复杂 math 数组 结果 等于 bilibili
原文地址:https://www.cnblogs.com/FHC1994/p/13029765.html