标签:编程技巧 原因 占用 简单 ali quic 原地排序 pre ble
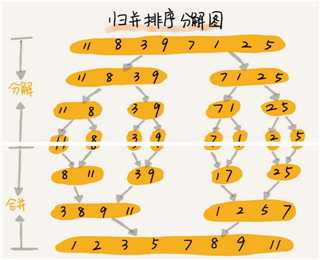
/**
* 归并排序
* @param arr 排序数据
* @param n 数组大小
*/
public static void merge_sort(int[] arr, int n) {
merge_sort_c(arr, 0, n - 1);
}
// 递归调用函数
public static void merge_sort_c(int[] arr, int p, int r) {
// 递归终止条件
if (p >= r) {
return;
}
// 取p到r之间的中间位置q
int q = (p + r) / 2;
// 分治递归
merge_sort_c(arr, p, q);
merge_sort_c(arr, q + 1, r);
// 将 arr[p...q] 和 arr[q+1...r] 合并为 arr[p...r]
merge(arr[p...r],arr[p...q],arr[q + 1...r]);
}
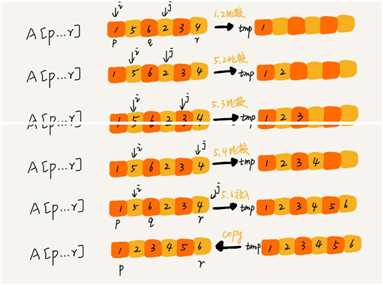
/**
* merge 合并函数
* @param arr 数组
* @param p 数组头
* @param q 数组中间位置
* @param r 数组尾
*/
public static void merge(int[] arr, int p, int q, int r) {
if (r <= p) return;
// 初始化变量i j k
int i = p;
int j = q + 1;
int k = 0;
// 申请一个大小跟A[p...r]一样的临时数组
int[] tmp = new int[r - p + 1];
// 比较排序移动到临时数组
while ((i <= q) && (j <= r)) {
if (arr[i] <= arr[j]) {
tmp[k++] = arr[i++];
} else {
tmp[k++] = arr[j++];
}
}
// 判断哪个子数组中有剩余的数据
int start = i, end = q;
if (j <= r) {
start = j;
end = r;
}
// 将剩余的数据拷贝到临时数组tmp
while (start <= end) {
tmp[k++] = arr[start++];
}
// 将tmp中的数组拷贝回 arr[p...r]
for (int a = 0; a <= r - p; a++) {
arr[p + a] = tmp[a];
}
}
/**
* 快速排序
* @param arr 排序数组
* @param p 数组头
* @param r 数组尾
*/
public static void quickSort(int[] arr, int p, int r) {
if (p >= r)
return;
// 获取分区点 并移动数据
int q = partition(arr, p, r);
quickSort(arr, p, q - 1);
quickSort(arr, q + 1, r);
}
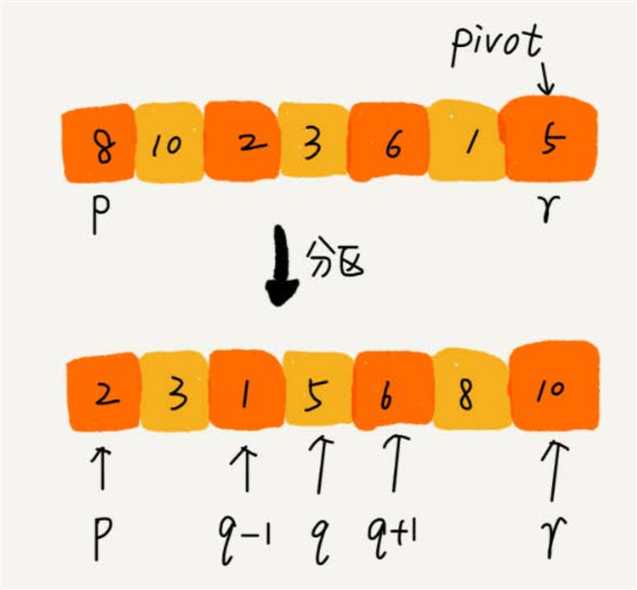
partition() 分区函数:
partition() 的实现有两种方式:
一种是不考虑空间消耗,此时非常简单。
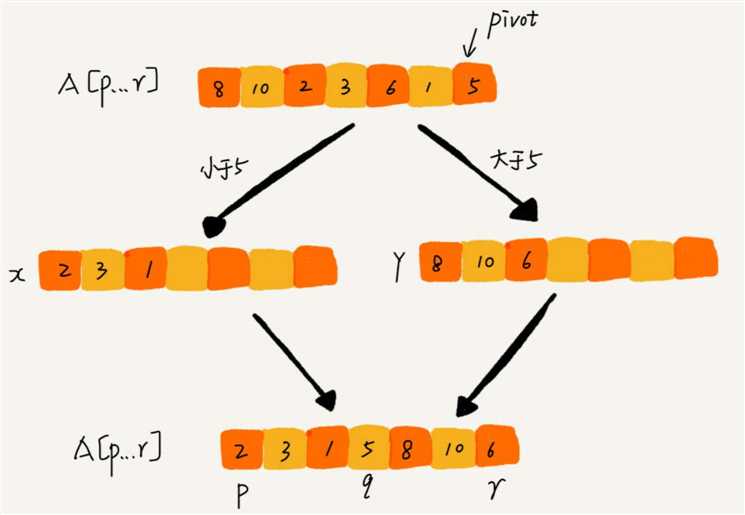
/**
* 分区函数方式一
*
* @param arr 数组
* @param p 上标
* @param r 下标
* @return 函数返回 pivot 的下标
*/
public static int partition1(int[] arr, int p, int r) {
int[] xArr = new int[r - p + 1];
int x = 0;
int[] yArr = new int[r - p + 1];
int y = 0;
int pivot = arr[r];
// 将小于 pivot 的元素都拷贝到临时数组 X,将大于 pivot 的元素都拷贝到临时数组 Y
for (int i = p; i < r; i++) {
// 小于 pivot 的存入 xArr 数组
if (arr[i] < pivot) {
xArr[x++] = arr[i];
}
// 大于 pivot 的存入 yArr 数组
if (arr[i] > pivot) {
yArr[y++] = arr[i];
}
}
int q = x + p;
// 再将数组 X 和数组 Y 中数据顺序拷贝到 arr[p…r]
for (int i = 0; i < x; i++) {
arr[p + i] = xArr[i];
}
arr[q] = pivot;
for (int i = 0; i < y; i++) {
arr[q + 1 + i] = yArr[i];
}
return q;
}
另外一种有点类似选择排序。

/**
* 分区函数方式二
* @param arr 数组
* @param p 上标
* @param r 下标
* @return 函数返回pivot的下标
*/
public static int partition2(int[] arr, int p, int r) {
int pivot = arr[r];
int i = p;
for (int j = p; j < r; j++) {
if (arr[j] < pivot) {
if (i == j) {
++i;
} else {
int tmp = arr[i];
arr[i++] = arr[j];
arr[j] = tmp;
}
}
}
int tmp = arr[i];
arr[i] = arr[r];
arr[r] = tmp;
return i;
}
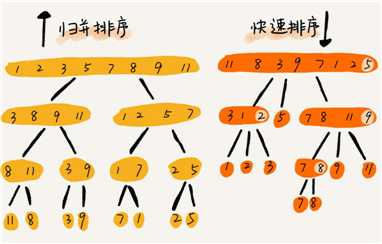
| 归并排序 | 快速排序 | |
|---|---|---|
| 排序思想 | 处理过程由下到上,先处理子问题,然后在合并 | 由上到下,先分区,在处理子问题 |
| 稳定性 | 是 | 否 |
| 空间复杂度 | Q(n) | Q(1) 原地排序算法 |
| 时间复杂度 | 都为 O(nlogn) | 平均为 O(nlogn),最差为 O(n2) |
标签:编程技巧 原因 占用 简单 ali quic 原地排序 pre ble
原文地址:https://www.cnblogs.com/xiexiandong/p/13046825.html