用欧拉计划学Rust编程语言（第700题：Eulercoin）

标签：不用   序列   loading   完成   ima   算法   规律   ons   mod   

问题描述：
欧拉诞生于1707年4月15日，对于序列(1504170715041707 * n) mod 4503599627370517，如果一个元素小于前面发现的所有Eulercoin，则其称为Eulercoin。

例如，第一个元素是1504170715041707，为第一个Eulercoin，第二个元素为3008341430083414，由于它大于1504170715041707，所以不是Eulercoin。然而，第三个元素为8912517754604，比前面的数都小，被称为Eulercoin。前两个Eulercoins之和是1513083232796311。

求所有Eulercoin之和。

解题过程：

第一步，先根据题意暴力求解

这个代码非常容易写出来。

const INC: u64 = 1504170715041707_u64;
const MOD: u64 = 4503599627370517_u64;

let mut x = 0_u64;
let mut min = INC;
for n in 1_u64.. {
    x = (x + INC) % MOD;
    if x <= min {
        min = x;
        println!("{:20} {:20}", n, x);
    }
}

运行这个程序，可以输出如下结果。

                   1     1504170715041707
                   3        8912517754604
                 506        2044785486369
                2527        1311409677241
                4548         578033868113
               11117         422691927098
               17686         267349986083
               24255         112008045068
               55079          68674149121
               85903          25340253174
              202630           7346610401
              724617           4046188430
             1246604            745766459
             6755007            428410324
            12263410            111054189
            42298633             15806432
           326125654             15397267
           609952675             14988102
           893779696             14578937
          1177606717             14169772
          1461433738             13760607
          1745260759             13351442
          2029087780             12942277
          2312914801             12533112
          2596741822             12123947
          2880568843             11714782
          3164395864             11305617
          3448222885             10896452
          3732049906             10487287
          4015876927             10078122
          4299703948              9668957
          4583530969              9259792
          4867357990              8850627
          5151185011              8441462
          5435012032              8032297
          5718839053              7623132
          6002666074              7213967
          6286493095              6804802
          6570320116              6395637
          6854147137              5986472
          7137974158              5577307
          7421801179              5168142
          7705628200              4758977
          7989455221              4349812
          8273282242              3940647
          8557109263              3531482
          8840936284              3122317
          9124763305              2713152
          9408590326              2303987
          9692417347              1894822
          9976244368              1485657
         10260071389              1076492
         10543898410               667327
         10827725431               258162
             … … … …              … … … …

越往后，想找到一个Eulercoin愈发困难，必须得改进算法。

第二步，找规律

在n=2527之后，后一个eulercoin与前一个eulercoin有着递推的关系，补上一些数字之后，就能发现更为明显的关系。比如，n=2021, 6569, 30824, 116727…时，得到的数虽然不是eulercoin，但数值非常大，与4503599627370517越来越接近。

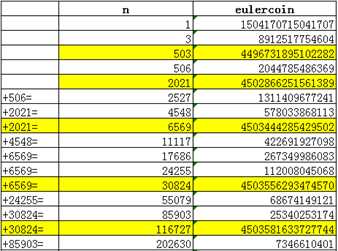
根据发现的规律，需要保存好最小的数和最大的数，不用一个数一个数的计算，效率非常高，不到1秒计算完成。

let mut sum = 1504170715041707_u64 + 8912517754604_u64 + 2044785486369_u64 + 1311409677241_u64;
let mut n_max = 2021_u64;
let mut max = 4502866251561389_u64;
let mut n = 2527_u64;
let mut x = 1311409677241_u64;
let mut min = x;

while min > 0 {
    let temp_n = n + n_max;
    let temp_x = (x + max) % 4503599627370517_u64;
    if temp_x <= min {
        n = temp_n;
        x = temp_x;
        min = x;
        sum += x;
        println!("{:20} {:12} {:20}", n, x, sum);
    }
    if temp_x > max {
        n_max = temp_n;
        max = temp_x;
        //println!("max: {} {} ", n_max, max);
    }
}

?

再优化

看了欧拉论坛中的优秀贴子，发现n的索引值并不需要记录，代码还可以更优美一些。

let inc = 1504170715041707_u64;
let modular = 4503599627370517_u64;
let mut low = inc;
let mut high = inc;
let mut sum = inc;
while low > 0 {
    let next = (low + high) % modular;
    if next < low {
        low = next;
        sum += low;
        println!("{:20} {:20}", low, sum);
    } else {
        high = next;
    }
}
println!("{}", sum);

用欧拉计划学Rust编程语言（第700题：Eulercoin）

标签：不用   序列   loading   完成   ima   算法   规律   ons   mod   

原文地址：https://www.cnblogs.com/speeding/p/rust_euler_700.html