标签：时间   数据   耗资源   数据结构   问题   英语   执行   实验环境   时间复杂度排序   

算法

定义

对特定问题求解方法和步骤的一种描述，它是指令的有限序列。

每个指令表示一个或多个操作。

描述

• 自然语言：英语、中文
• 流程图：传统流程图、NS流程图
• 伪代码：类语言：类C语言
• 程序代码：高级语言

算法与程序

• 算法是解决问题的一种方法或一个过程，考虑输入与输出，一个问题由多种算法。
• 程序是用程序设计语言对算法的实现。

程序 = 数据结构 + 算法

算法特性

• 有穷性：一个算法必须总是在执行有穷步之后结束，且每一步都在有穷时间内完成。（算法不能是死循环）
• 确定性：算法中的每一条指令必须有确切的含义，没有二义性，在任何条件下，只有唯一的一条执行路径，即对于相同的输入只能得到相同的输出。（指令不能含糊不清）
• 可行性：算法是可执行的，算法描述的操作可以通过已经实现的基本操作执行有限此来实现。（指令复用）
• 输入：算法有零个或多个输入。（可以不用输入）
• 输出：算法有一个或多个输出。（必须要有输出）

设计算法的要求

• 正确性：程序对于精心选择的、典型、苛刻且带有刁难性的几组输入数据能够得出满足要求的结果；（选取具有代表性的数据对算法进行测试）
• 可读性：算法应该便于人的理解，可以较为容易看懂，晦涩难读的算法，不便于维护。（算法应该浅显易懂）
• 健壮性：当输入非法数据时，算法能做出相应处理，处理出错的方式，应该返回一个表示错误或错误性质的值，不应中断程序的执行。（对输入错误数据做出相应的处理）
• 高效性：耗时要少，占用存储空间要低。

算法分析

算法时间效率的度量

根据该算法编制的程序在计算机上执行的耗时来度量。

两种度量方法

事后统计

将算法实现为程序，在计算机上运行，观测其耗时和占用存储空间大小。（实验环境的影响较大，结果与计算机软硬件有关，误差较大）

事前分析

对算法所耗资源的估算。

算法运行时间 = 一个简单操作所需的时间 x 简单操作次数

? = Σ每条语句的执行次数 x 该语句执行一次所需的时间

? = Σ每条语句频度 x 该语句执行一次所需的时间（假定为单位时间）

? = Σ每条语句频度

例子

算法时间复杂度的渐进表示法

若有某个辅助函数f(n)，使得当n趋近于无穷大时，T(n)/f(n)的极限值为不等于零的常数，则称f(n)是T(n)的同数量级函数。记作T(n) = O(f(n))，称O(f(n))为算法的渐进时间复杂度(O是数量级的符号)，简称时间复杂度

只考虑算法中基本操作执行的次数。

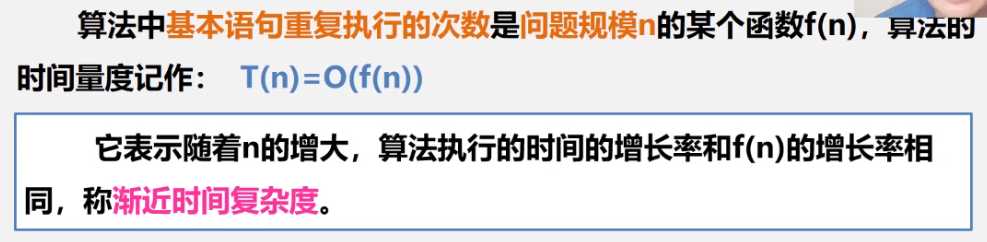
基本语句指算法中执行次数最多的那个语句。（次数随输入数据集变化）

问题规模n：

• 排序：n为记录数
• 矩阵：n为矩阵的阶数
• 多项式：n为多项式的项数
• 集合：n为元素个数
• 树：n为树的结点个数
• 图：n为图的顶点数或边数

最坏时间复杂度：最坏情况下，算法的时间复杂度。

平均时间复杂度：在所有可能输入实例在等概率出现的情况下，算法的期望运行时间。

最好时间复杂度：最好情况下，算法的时间复杂度。

考虑优先级：最坏时间复杂度 > 平均时间复杂度 > 最好时间复杂度

注：对于复杂的算法，需要将其拆分，然后利用加法、乘法法则计算其数量级。

• 加法法则：将复杂函数，能够拆分为两个函数的数量级和，则取数量级最大的那个。

  T(n) = T1(n) + T2(n) = O(f(n)) + O(g(n)) = O(max(f(n),g(n)))

• 乘法法则：将复杂函数，能够拆分为两个函数的数量级积，则取两个函数的数量级积。

  T(n) = T1(n) x T2(n) = O(f(n)) x O(g(n)) = O(f(n) x g(n))

各数量级时间复杂度排序（从小到大）：

空间复杂度度量

渐进空间复杂度

算法所需存储空间的度量

S(n) = O(f(n))

注：n为问题的规模

• 算法本身要占据的空间，输入/输出，指令，常数，变量等。
• 算法要使用的辅助空间。

数据结构-算法

标签：时间   数据   耗资源   数据结构   问题   英语   执行   实验环境   时间复杂度排序   

原文地址：https://www.cnblogs.com/lisztomania/p/13086472.html