标签:规则 mamicode 科学 lin 构造 state 缩小 最大 prepare
递归一词还较为常用于描述以自相似方法重复事物的过程。
在数学和计算机科学中,递归指由一种(或多种)简单的基本情况定义的一类对象或方法,并规定其他所有情况都能被还原为其基本情况。
斐波那契数列是典型的递归案例,递归 是一种特殊的 循环,通过函数体来进行的循环
示例:
# 计算 n!
n! = 1 * 2 * 3 * ... * n
?
def Factorial(n):
if n <=1:
return 1
return n * Factorial(n - 1)
def recursion(level,param1,param2,...):
# recursion terminator 1.递归终结者,递归中止的条件
if level > MAX_LEVEL:
process_result
return
?
# process logic in current level 2.处理当前层逻辑
process(level,data...)
?
# drill down 3.下探到下一层
self.recursion(level + 1,p1,...)
?
#reverse the current level status if needed 4.清理当前层(比如需要清理的全局变量),不是必选项
递归终止条件(terminator):写递归函数开始的话,一定要先把函数递归终止条件写上,否则,会导致无限递归或者死循环。
处理当前层的逻辑(current level logic):完成这一层要进行的业务代码、逻辑代码
下探到下一层(drill down):这里的参数来标记当前是哪一层,这里level必须加1,同时把相应的参数p1、p2、p3...放下去就行了。
清理(reverse):递归完了,有些东西可能要清理,(非必需)
不要人肉进行递归(最大误区),初学者可以在纸上画出递归的状态树,慢慢熟练之后一定要抛弃这样的习惯。一定要记住:直接看函数本身开始写即可。否则,永远没办法掌握、熟练使用递归。
找到最近最简的方法,将其拆解成可重复解决的问题(找最近重复子问题)。原因是我们写的程序的指令,只包括 if else 、 for 和 while loop、递归调用。
数学归纳法的思维,最开始最简单的条件是成立的,比如n=1,n=2的时候是成立的,且第二点你能证明当n成立的时候,可以推导出n+1也成立的。
分治和回溯,本质上就是递归,是递归的一个细分类。可以理解为分治和回溯,就是一种特殊的递归,或者是较为复杂的递归。
本质上就是找重复性以及分解问题,和最后组合每个子问题的结果,都是这一个思路。
碰到一个题目,就会找到他的重复性:
最优重复性:动态规划
最近重复性:根据重复性的构造和分解,便有分治和回溯。
分治的思想:本质是递归,在递归状态树的时候,对一个问题会化解成好几个子问题。
在计算机科学中,分治法是一种很重要的算法。字面上的解释是“分而治之”,就是把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并。这个技巧是很多高效算法的基础,如排序算法(快速排序,归并排序),傅立叶变换(快速傅立叶变换)
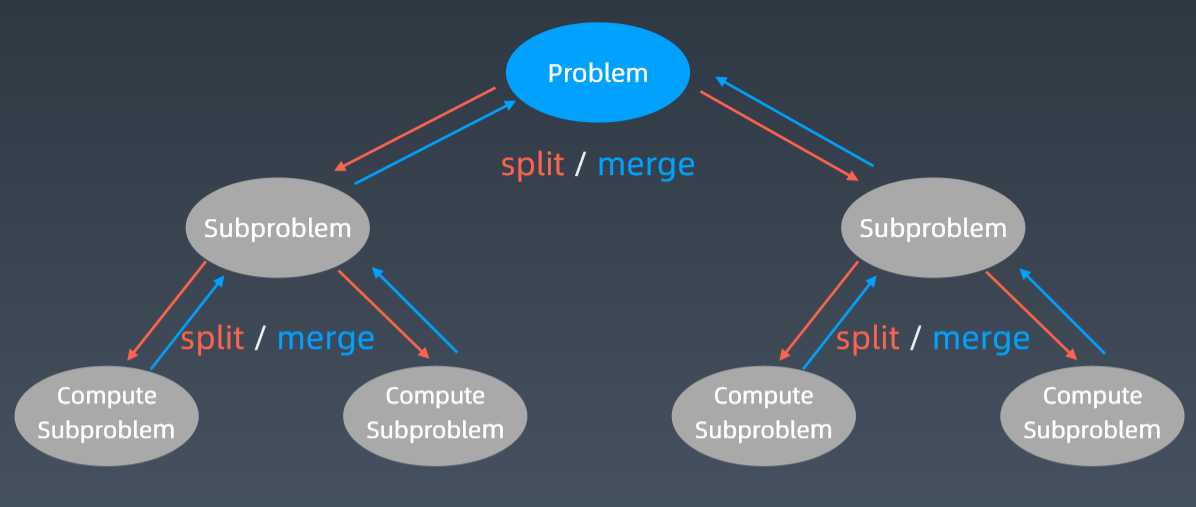
分治法的设计思想是:将一个难以直接解决的大问题,分割成一些规模较小的相同问题,以便各个击破,分而治之。
分治策略是:对于一个规模为n的问题,若该问题可以容易地解决(比如说规模n较小)则直接解决,否则将其分解为k个规模较小的子问题,这些子问题互相独立且与原问题形式相同,递归地解这些子问题,然后将各子问题的解合并得到原问题的解。这种算法设计策略叫做分治法。
分治法所能解决的问题一般具有以下几个特征: 1) 该问题的规模缩小到一定的程度就可以容易地解决 2) 该问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构性质。 3) 利用该问题分解出的子问题的解可以合并为该问题的解; 4) 该问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子子问题。 第一条特征是绝大多数问题都可以满足的,因为问题的计算复杂性一般是随着问题规模的增加而增加; 第二条特征是应用分治法的前提它也是大多数问题可以满足的,此特征反映了递归思想的应用;、 第三条特征是关键,能否利用分治法完全取决于问题是否具有第三条特征,如果具备了第一条和第二条特征,而不具备第三条特征,则可以考虑用贪心法或动态规划法。 第四条特征涉及到分治法的效率,如果各子问题是不独立的则分治法要做许多不必要的工作,重复地解公共的子问题,此时虽然可用分治法,但一般用动态规划法较好。
分治算法就是将原问题划分成n个规模较小,并且结构与原问题相似的子问题,递归地解决这些子问题,然后再合并其结果,就得到原问题的解。
分治算法的递归实现中,每一层递归都会涉及这样三个操作:
分解:将原问题分解成一系列子问题
解决:递归地求解各个子问题,若子问题足够小,则直接求解
合并:将子问题的结果合并成原问题
分治算法能解决的问题,一般需要满足下面这几个条件:
原问题与分解成的小问题具有相同的模式
原问题分解成的子问题可以独立求解,子问题之间没有相关性
具有分解终止条件,也就是说,当问题足够小,可以直接求解
可以将子问题合并成原问题,而这个合并操作的复杂度不能太高,否则就起不到减小算法总体复杂度的效果了
def divide_conquer(problem, param1, param2, ...):
# recursion terminator 终止条件
if problem is None:
print_result
return
# prepare data 处理当前层逻辑
data = prepare_data(problem)
subproblems = split_problem(problem, data)
# conquer subproblems 调用函数下探到下一层,解决更细节的子问题
subresult1 = self.divide_conquer(subproblems[0], p1, ...)
subresult2 = self.divide_conquer(subproblems[1], p1, ...)
subresult3 = self.divide_conquer(subproblems[2], p1, ...)
...
# process and generate the final result
result = process_result(subresult1, subresult2, subresult3, ...)
?
# revert the current level states
# 与泛型递归不同就是在drill down与revert state中间加了一步
# ---> 就是把drill down得到的子结果要合并在一起,返回回去。
回溯的处理思想有点类似枚举搜索。通过枚举所有的解,找到满足期望的解。为了有规律地枚举所有可能的解,避免遗漏和重复,我们把问题求解的过程分为多个阶段。每个阶段,都会面对一个岔路口,我们先随意选一条路走,当发现这条路走不通的时候(不符合期望的解),就回退到上一个岔路口,另选一种走法继续走。
回溯法是一种选优搜索法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。
许多复杂的,规模较大的问题都可以使用回溯法,有“通用解题方法”的美称。
回溯可以理解为递归的一种问题,不断地在每一层去试,每一层有不同的办法,类似于一个一个去试,看这个方法是否可行。最典型的应用是八皇后问题、数独。
在包含问题的所有解的解空间树中,按照深度优先搜索的策略,从根结点出发深度探索解空间树。当探索到某一结点时,要先判断该结点是否包含问题的解,如果包含,就从该结点出发继续探索下去,如果该结点不包含问题的解,则逐层向其祖先结点回溯。(其实回溯法就是对隐式图的深度优先搜索算法)。
若用回溯法求问题的所有解时,要回溯到根,且根结点的所有可行的子树都要已被搜索遍才结束。
而若使用回溯法求任一个解时,只要搜索到问题的一个解就可以结束。
(1)针对所给问题,确定问题的解空间:
首先应明确定义问题的解空间,问题的解空间应至少包含问题的一个(最优)解。
(2)确定结点的扩展搜索规则
(3)以深度优先方式搜索解空间,并在搜索过程中用剪枝函数避免无效搜索。
回溯法采用试错的思想,它尝试分布的去解决一个问题。在分步解决问题的过程中,当它通过尝试发现现有的分步答案不能得到有效的正确的解答的时候,它将取消上一步甚至是上几步的计算,再通过其他的可能的分步解答再次尝试寻找问题的答案。
回溯法通常用最简单的递归方法来实现,在反复重试上述的步骤后可能出现两种情况:
找到一个可能存在的正确的答案;
在尝试了所有可能的分步方法后宣告该问题没有答案。 在最坏的情况下,回溯法会导致一次复杂度为指数时间的计算。
参考资料
[1]https://blog.csdn.net/qq_40378034/java/article/details/102764545
[2]https://www.cnblogs.com/yddzyy/p/5587643.html
算法漫游指北(第十篇):泛型递归、递归代码模板、递归思维要点、分治算法、回溯算法
标签:规则 mamicode 科学 lin 构造 state 缩小 最大 prepare
原文地址:https://www.cnblogs.com/Nicholas0707/p/13138193.html