标签:lib return 数据结构 isp 情况下 提前 bsp spl 推理
一、如何分析一个“排序算法”
从三个维度进行评价和分析:
1. 排序算法的执行效率
a. 最好情况、最坏情况、平均情况时间复杂度
b. 时间复杂度的系统、常数、低阶
c. 比较次数和交换(或移动)次数
2. 排序算法的内存消耗
用空间复杂度来衡量。
原地排序算法,特指空间复杂度是O(1)的排序算法。
3. 排序算法的稳定性
稳定的排序算法:相同元素的前后顺序没有改变的排序算法
反之叫不稳定的排序算法。
二、冒泡排序
冒泡排序只会操作相邻的两个数据。每次冒泡操作都会对相邻的两个元素进行比较,如果不满足大小关系就互换。
/// <summary>
/// 冒泡排序,a表示数组,n表示数组大小
/// </summary>
/// <param name="a">数组</param>
/// <param name="n">数组大小</param>
public static void BubbleSort(int[] a, int n)
{
if (n <= 1) return;
for (int i = 0; i < n; ++i)
{
// 提前退出冒泡循环的标志位
bool flag = false;
for (int j = 0; j < n - i - 1; ++j)
{
if (a[j] > a[j + 1])
{ // 交换
int tmp = a[j];
a[j] = a[j + 1];
a[j + 1] = tmp;
flag = true; // 表示有数据交换
}
}
if (!flag) break; // 没有数据交换,提前退出
}
}
分析排序算法的三个方面:
1. 冒泡排序是原地排序算法吗?
冒泡的过程只涉及到相邻数据的交换,只需要常量级的临时空间,即空间复杂度为O(1),是原地排序算法。
2. 冒泡排序是稳定的排序算法吗?
冒泡的过过,只交换不满足大小关系的元素,相等的两个元素不做交换,是稳定的排序算法。
3. 冒泡排序的时间复杂度是多少?
最好情况时间复杂度:O(n)。数据是有序的,只需要进行一次冒泡操作。
最坏情况时间复杂度:O(n2)。数据是倒序的,要进行n次冒泡操作。
平均情况时间复杂度:O(n2)
三、关于平均时间复杂度
如果用概率论方法定量分析平均时间复杂谎,涉及的数学推理和计算就会很复杂。下面介绍另外一种思路:通过“有序度”和“逆序度”两个概念进行分析。
有序度:是数据中具有有序关系的元素对的个数。
有序元素对:a[i] <= a[j],如果i < j。
满有序度:完全有序的数组的有序度。
逆序度:与有序度相反。
逆序元素对:a[i] > a[j],如果i < j。
以上概念得到一个公式:逆序度 = 满有序度 - 有序度
排序算法中,主要包含两个操作原子,比较和交换。不管算法怎么改进,交换次数总是确定的,即为逆序度,也就是n*(n-1)/2 - 初始有序度。
对于包含n个数据的数组进行冒泡排序,平均交换次数 = (最好情况 + 最坏情况)/2 = n*(n-1)/4。
平均情况下,比较操作肯定比交换操作要多,而复杂度上限是O(n2),所以平均情况时间复杂度是O(n2)。
四、插入排序
算法思路:往有序的数组里插入数据,找到插入位置,再移动后续的数据,即可完成。为此把数组分为两个区间,已排序区间和未排序区间。初始已排序区间只有一个元素,即数组的第一个元素,然后再遍历未排序区间(除第一个元素外的数组),把元素插入到已排序区间。
/// <summary>
/// 插入排序,a表示数组,n表示数组大小
/// </summary>
/// <param name="a">数组</param>
/// <param name="n">数组大小</param>
public static void InsertionSort(int[] a, int n)
{
if (n <= 1) return;
for (int i = 1; i < n; ++i)
{
int value = a[i];
int j = i - 1;
// 查找插入的位置
for (; j >= 0; --j)
{
if (a[j] > value)
{
a[j + 1] = a[j]; // 数据移动
}
else
{
break;
}
}
a[j + 1] = value; // 插入数据
}
}
分析排序算法的三个方面:
1. 插入排序是原地排序算法吗?
空间复杂度为O(1),是原地排序算法。
2. 插入排序是稳定的排序算法吗?
插入时选择将后面出现的元素插入到前面出现元素的后面,这样原有前后顺序不变,是稳定的排序算法。
3. 插入排序的时间复杂度是多少?
最好情况时间复杂度:O(n)。数据是有序的,只需要遍历一次。
最坏情况时间复杂度:O(n2)。数据是倒序的,要进行n次遍历和移动操作。
平均情况时间复杂度:O(n2)。数组中插入一个数据的平均时间复杂度是O(n),循环执行n次,即平均时间复杂度为O(n2)
五、选择排序
选择排序算法的实现思路类似插入排序。分已排序区间和未排序区间,每次从未排序区间中找到最小的元素,将其放到已排序区间的末尾。
/// <summary>
/// 选择排序,a表示数组,n表示数组大小
/// </summary>
/// <param name="a">数组</param>
/// <param name="n">数组大小</param>
public void SelectionSort(int[] a, int n)
{
if (n <= 1) return;
for (int i = 0; i < n - 1; i++)
{
int value = a[i];
// 找到第i个最小值
for (int j = i + 1; j < n; j++)
{
if (value > a[j])
{
// 交换两值的位置
int temp = value;
value = a[j];
a[j] = temp;
}
}
// 把第i个最小值放到第i位
a[i] = value;
}
}
分析排序算法的三个方面:
1. 选择排序是原地排序算法吗?
空间复杂度为O(1),是原地排序算法。
2. 选择排序是稳定的排序算法吗?
不是,选择交换的元素可能会破坏相等元素的原有顺序。
3. 选择排序的时间复杂度是多少?
最好情况时间复杂度:O(n2)。对于有序数组,仍然需要做n遍的遍历比较。
最坏情况时间复杂度:O(n2)。对于逆序数组,需要做n遍的遍历比较和交换。
平均情况时间复杂度:O(n2)。最好情况和最坏情况都是O(n2),平均也是O(n2)
六、为什么插入排序要比冒泡排序更受欢迎
冒泡排序不管怎么优化,元素交换的次数是一个固定值,是原始数据的逆序度。
插入排序不管怎么优化,元素移动的次数也等于原始数据的逆序度。
但在代码实现上,冒泡排序的数据交换要比插入排序的数据移动要复杂。冒泡排序需要3个赋值操作,而插入排序只需要1个。
冒泡排序中数据的交换操作:
if (a[j] > a[j+1]) { // 交换
int tmp = a[j];
a[j] = a[j+1];
a[j+1] = tmp;
flag = true;
}
插入排序中数据的移动操作:
if (a[j] > value) {
a[j+1] = a[j]; // 数据移动
} else {
break;
}
在大量数据的排序时,这一点点的差距就会放大,在性能要求高的环境,首先插入排序。
七、内容小结
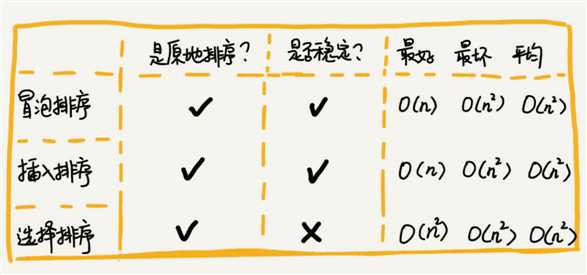
八、课后思考
我们讲过,特定算法是依赖特定的数据结构的。我们今天讲的几种排序算法,都是基于数组实现的。如果数据存储在链表中,这三种排序算法还能工作吗?如果能,那相应的时间、空间复杂度又是多少呢?
基于链表可以实现。
单链表之冒泡算法:
/// <summary>
/// 单链表冒泡排序
/// </summary>
public static void BubbleSortByLinkedList(MyLinkedListNode head)
{
if (head == null || head.Next == null || head.Next.Next == null) return;
MyLinkedListNode curr = head.Next;
while (curr != null)
{
// 提前退出冒泡循环的标志位
bool flag = false;
MyLinkedListNode node = curr.Next;
while (node != null)
{
if (curr.Data > node.Data)
{
// 交换
int temp = curr.Data;
curr.Data = node.Data;
node.Data = temp;
flag = true; // 表示有数据交换
}
node = node.Next;
}
if (!flag) break; // 没有数据交换,提前退出
curr = curr.Next;
}
}
最好情况时间复杂度:O(n)
最坏情况时间复杂度:O(n2)
平均情况时间复杂度:O(n2)
空间复杂度:O(1)
单链表之插入排序:
/// <summary>
/// 单链表插入排序
/// </summary>
public static void InsertionSortByLinkedList(MyLinkedListNode head)
{
if (head == null || head.Next == null || head.Next.Next == null) return;
MyLinkedListNode notSort = head.Next.Next;
while (notSort != null)
{
MyLinkedListNode sorted = head.Next;
MyLinkedListNode prevSorted = head;
bool flag = false;
while (sorted != null)
{
if (sorted.Data > notSort.Data)
{
var temp = notSort.Next;
prevSorted.Next = notSort;
notSort.Next = sorted;
notSort = temp;
flag = true;
break;
}
prevSorted = sorted;
sorted = sorted.Next;
}
if (!flag) notSort = notSort.Next;
}
}
最好情况时间复杂度:O(n2)
最坏情况时间复杂度:O(n2)
平均情况时间复杂度:O(n2)
空间复杂度:O(1)
单链表之选择排序:
/// <summary>
/// 单链表选择排序
/// </summary>
public static void SelectionSortByLinkedList(MyLinkedListNode head)
{
if (head == null || head.Next == null || head.Next.Next == null) return;
MyLinkedListNode selected = head;
while (selected != null)
{
MyLinkedListNode currNode, prevNode, minNode, prevMinNode;
prevNode = prevMinNode = selected;
currNode = minNode = selected.Next;
bool flag = false;
// 找到最小值结点和前置结点
while (currNode != null)
{
if (currNode.Data < minNode.Data)
{
prevMinNode = prevNode;
minNode = currNode;
flag = true;
}
prevNode = currNode;
currNode = currNode.Next;
}
if (flag)
{
MyLinkedListNode changedNode = selected.Next; // 临时记录待交换结点,以便进行结点交换时进行赋值
MyLinkedListNode minNextNode = minNode.Next; // 临时保存待交换最小结点的Next
// 相邻两元素交换
if (changedNode.Next == minNode)
{
selected.Next = minNode; // 已选择区间链接上最小结点
minNode.Next = changedNode;
changedNode.Next = minNextNode;
}
else
{
selected.Next = minNode; // 已选择区间链接上最小结点
minNode.Next = changedNode.Next;
prevMinNode.Next = changedNode;
changedNode.Next = minNextNode;
}
}
selected = selected.Next;
}
}
最好情况时间复杂度:O(n2)
最坏情况时间复杂度:O(n2)
平均情况时间复杂度:O(n2)
空间复杂度:O(1)
《数据结构与算法之美》08——排序(一)冒泡排序、插入排序、选择排序
标签:lib return 数据结构 isp 情况下 提前 bsp spl 推理
原文地址:https://www.cnblogs.com/liang24/p/13162023.html