标签:param inf 字符 stack 运算符 while 优先 操作符 优先级
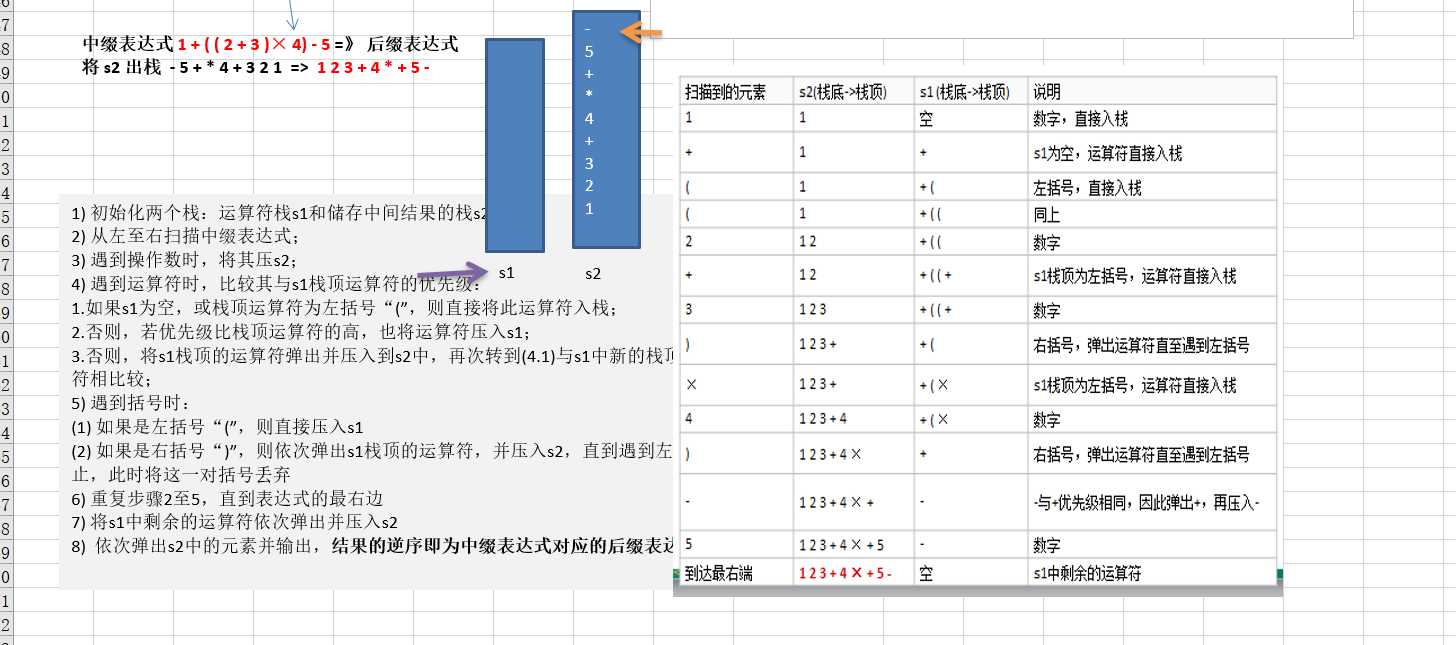
1)初始化两个栈:运算符栈s1和储存中间结果的栈s2;
2)从左至右扫描中缀表达式;
3)遇到操作数时,将其压s2;
4)遇到运算符时,比较其与s1栈顶运算符的优先级:
(1)如果s1为空,或栈顶运算符为左括号“(”,则直接将此运算符入栈;
(2)否则,若优先级比栈顶运算符的高,也将运算符压入s1;
(3)否则,将s1栈顶的运算符弹出并压入到s2中,再次转到(4-1)与s1中新的栈顶运算符相比较;
5)遇到括号时:
(1)如果是左括号“(”,则直接压入s1
(2)如果是右括号“)”,则依次弹出s1栈顶的运算符,并压入s2,直到遇到左括号为止,此时将这一对括号丢弃
6)重复步骤2至5,直到表达式的最右边
7)将s1中剩余的运算符依次弹出并压入s2
8)依次弹出s2中的元素并输出,结果的逆序即为中缀表达式对应的后缀表达式
/// <summary> /// 字符串转中缀表达式的List /// </summary> /// <param name="expression"></param> /// <returns></returns> public static List<string> ToInfixExpression(string expression) { List<string> list = new List<string>(); int index = 0; string str = ""; do { //48-57ASCII码代表的是0-9 如果不是0-9直接入链表 if (expression[index] < 48 || expression[index] > 57)//ascii编码 { list.Add("" + expression[index]); index++; } else { str = ""; //多位数判断 while (index < expression.Length && expression[index] >= 48 && expression[index] <= 57) { str += expression[index]; index++; } list.Add(str); } } while (index < expression.Length); return list; }
/// <summary> /// 中缀转后缀 /// </summary> /// <param name="expression"></param> /// <returns></returns> public static List<string> ParseSuffixExpression(List<string> expression) { //存储中间结果 List<string> list = new List<string>(); //符号栈 Stack<string> stack = new Stack<string>(); foreach (var item in expression) { //多位数判断 如果是数字直接加入list if (Regex.IsMatch(item, "\\d+")) { list.Add(item); } //如果是左括号,直接入符号栈 else if (item.Equals("(")) { stack.Push(item); } //如果是右括号 else if (item.Equals(")")) { //依次弹出stack栈顶的运算符,并存入list,直到遇到左括号为止 while (!stack.Peek().Equals("(")) { list.Add(stack.Pop()); } //将(也出栈 stack.Pop(); } //如果是*/+- else { //循环判断item的优先级小于或者等于stack栈顶运算符,将stack栈顶的运算符出栈并加入到list中 while (stack.Count != 0 && Operation.GetValue(stack.Peek()) >= Operation.GetValue(item)) { list.Add(stack.Pop()); } //将item入栈 stack.Push(item); } } //将stack剩余的运算符依次入list while (stack.Count!=0) { list.Add(stack.Pop()); } return list; }
public class Operation { private static int ADD = 1; private static int SUB = 1; private static int MUL = 2; private static int DIV = 2; public static int GetValue(string operation) { int result = 0; switch (operation) { case "+": result = ADD; break; case "-": result = SUB; break; case "*": result = MUL; break; case "/": result = DIV; break; default: // Console.WriteLine("不存在该运算符"); break; } return result; } }
/// <summary> /// 计算 /// </summary> /// <param name="list"></param> /// <returns></returns> public static int Calculate(List<string> list) { //创建栈 Stack<string> stack = new Stack<string>(); //循环遍历 list.ForEach(item => { //正则表达式判断是否是数字,匹配的是多位数 if (Regex.IsMatch(item,"\\d+")) { //如果是数字直接入栈 stack.Push(item); } //如果是操作符 else { //出栈两个数字,并运算,再入栈 int num1 =int.Parse(stack.Pop()); int num2 = int.Parse(stack.Pop()); int result = 0; if(item.Equals("+")) { result = num2 + num1; } else if(item.Equals("*")) { result = num2 * num1; } else if(item.Equals("/")) { result = num2 / num1; } else if (item.Equals("-")) { result = num2 - num1; } else { throw new Exception("无法识别符号"); } stack.Push(""+result); } }); //最后把stack中数据返回 return int.Parse(stack.Pop()); }
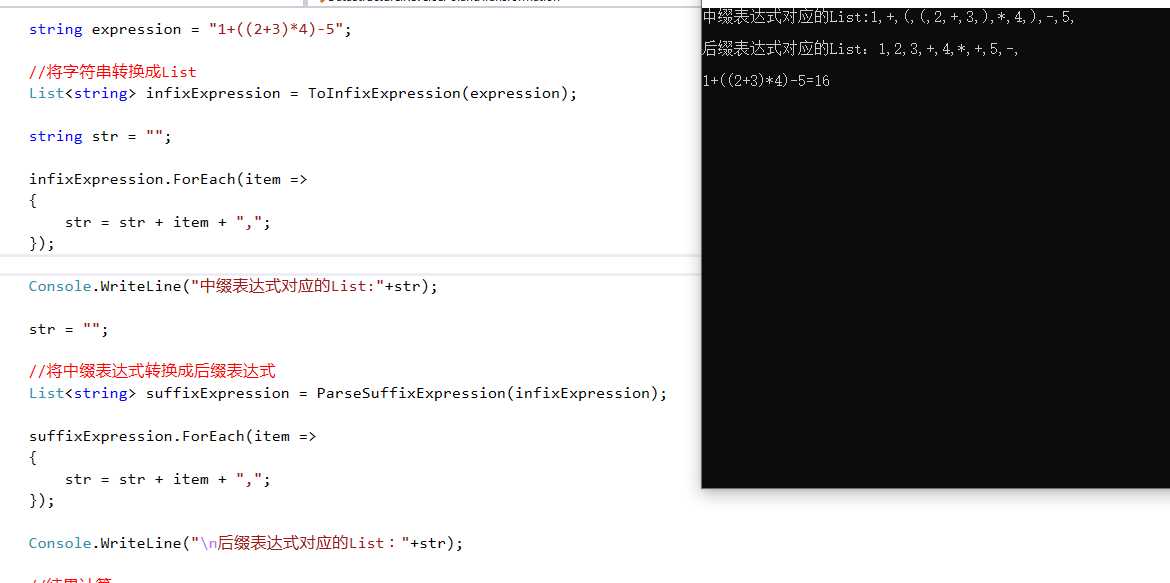
public class ReversePolandTransformation { public static void Test() { string expression = "1+((2+3)*4)-5"; //将字符串转换成List List<string> infixExpression = ToInfixExpression(expression); string str = ""; infixExpression.ForEach(item => { str = str + item + ","; }); Console.WriteLine("中缀表达式对应的List:"+str); str = ""; //将中缀表达式转换成后缀表达式 List<string> suffixExpression = ParseSuffixExpression(infixExpression); suffixExpression.ForEach(item => { str = str + item + ","; }); Console.WriteLine("\n后缀表达式对应的List:"+str); //结果计算 int result =PolandNotation.Calculate(suffixExpression); Console.WriteLine($"\n{expression}={result}"); } }
标签:param inf 字符 stack 运算符 while 优先 操作符 优先级
原文地址:https://www.cnblogs.com/vic-tory/p/13176657.html